Коэффициент множественной корреляции

После проверки модели на адекватность, необходимо убедиться в том, насколько хорошо регрессионная модель описывает отклик как функцию факторов. Это важное знание, дающее представление о том, оказывают ли влияние факторы на отклик.

Рассмотрим данную проблему на примере двух регрессионных моделей в форме полинома второго порядка от одного фактора 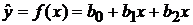, в которых различны коэффициенты 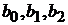. На рис. 8 представлен график первой модели 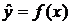. Из графика видно, что среднее значение отклика 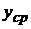нельзя сопоставить с 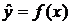, так как сумма ошибок отклонения будет значительной. Расположение точек на графике свидетельствует о зависимости отклика от .

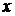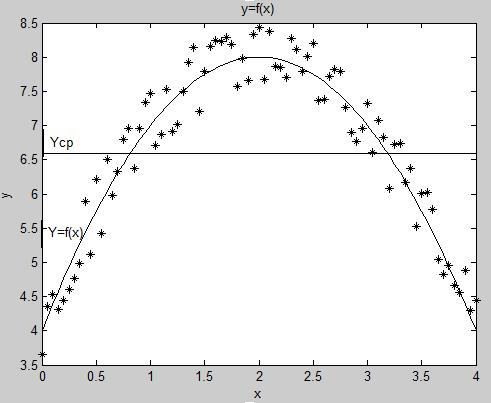
Рис. 8. Графическая интерпретация зависимости отклика от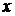

Во второмслучае (рис. 9) нельзя однозначно сделать вывод о зависимости отклика от 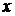, так как отклик 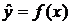слабо отличается от среднего значения .

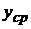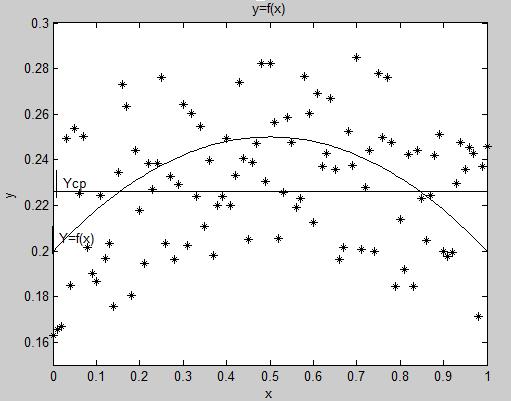
Рис. 9. Графическая интерпретация сомнительной зависимости отклика от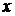

На основании рис. 9 можно сделать предположение о том факте, что не зависит от 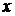. Это в свою очередь указывает на то, что оценки коэффициентов 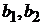в регрессионной модели отличны от нуля лишь за счет случайных возмущений. При этом 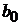будет являться оценкой среднего значения отклика 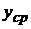. Вид регрессионной модели (рис. 9) может получиться при условии, что отклик не зависит от 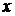, а является функцией другой переменной 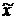, по каким либо причинам не включенной в исследование, но проявляющей свое влияние через случайную ошибку.

Данные рассуждения верны и для многофакторной регрессионной модели (4) 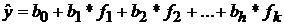. В данном случае проверяется гипотеза о том, что не являются ли 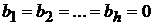, то есть существенно ли отличается предсказанный отклик от среднего .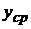

С целью оценки данного утверждения вводится коэффициент детерминации (мера определенности, выборочный коэффициент множественной корреляции, коэффициент детерминации) 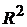(19), показывающий, на сколько предсказание по регрессионной модели лучше, чем по среднему значению отклика .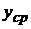

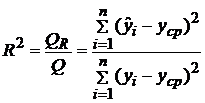(19)

В силу того, что 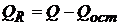, выражение (19) можно переписать в следующем виде 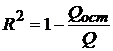(20).

(20)

Коэффициент множественной корреляции изменяется в интервале 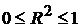. Рассмотрим два крайних случая:

1. 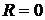- говорит о том, что все коэффициенты регрессионной модели кроме 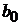равны нулю 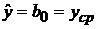. Из чего следует, что все регрессоры, включенные в модель не оказывают никакого влияния на отклик .

2. 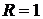- говорит о том, что отсутствуют случайные возмущения ( 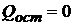), а предсказанный отклик всегда будет совпадать с истинным откликов .

По значению коэффициента 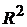(показывает долю изменчивости отклика , которая объясняется моделью) можно судить о работоспособности модели в целом. Из двух альтернативных моделей лучше та, у которой больше значение .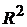

Пример.Если в результате вычислений получено значение 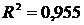, то уравнение регрессии объясняет 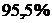результативного признака, а 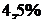объясняется прочими факторами.

Коэффициент 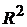нельзя использовать в том случае, когда число опытов меньше либо равно числу регрессоров 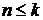. На практике 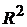практически никогда не достигает крайних случаев. В связи с этим необходимо понимание того, когда можно считать, что он получился отличным от нуля только из-за случайных возмущений.

Более определенно оценить качество уравнения регрессии в целом позволяет критерий Фишера. Проверяется это постановкой гипотезы о том, что не равно ли нулю 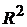, что указывает на равенство нулю всех коэффициентов, кроме 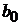. Для этого вводится отношение 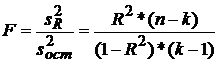(21).

(21)

Оценка значимости коэффициента множественной корреляции проводится следующим образом:

1. Вычисляются значения 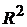по формулам (19) или (20) и 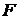по формуле (21).

2. Задается уровень значимости 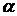и для чисел степеней свободы 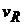и 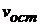по таблице Фишера находится 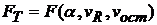и делаются следующие выводы:

- Если 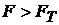, то 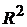значим и его значение нельзя объяснить только случайным возмущением.

- Если 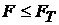, то 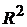незначим, следовательно, такой моделью нельзя воспользоваться для предсказания отклика.

Случай 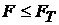указывает на то, что зависимость модели от регрессоров либо очень слаба, либо вовсе отсутствует, что возможно по двум причинам:

- В модель не включены сильно влияющие факторы, влияние которых проявляется только через остаточные ошибки .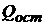

- В модель включены все существенные факторы, но при этом выбрана не корректная структура модели.

Таким образом, незначимость 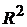является достаточным основанием отказа от модели. Однако, и тот факт, что 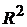значим, не доказывает что модель адекватна. Данный коэффициент является очень полезным в том случае, когда не удается проверить адекватность модели посредством реализации повторных опытов при одних и тех же условиях. В этих условиях 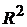может быть использован, как качественная характеристика полученной модели. В связи с тем, что решение о значимости/незначимости 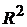принимается с учетом (21), нельзя утверждать, что большое значение 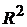говорит о значимости, а малое о незначимости. Иногда большое значение 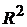может оказаться не значимым, а в некоторых случаях малое значение 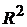значимо, так как все зависит от числа степеней свободы.