Проверка адекватности регрессионной модели.
Остаточная дисперсия 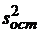 образуется посредством влияния случайного возмущения и неадекватности модели. Процедуру оценки адекватности регрессионной модели можно свести к сравнению остаточной дисперсии
образуется посредством влияния случайного возмущения и неадекватности модели. Процедуру оценки адекватности регрессионной модели можно свести к сравнению остаточной дисперсии 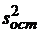 с независимой от нее оценкой
с независимой от нее оценкой  дисперсии случайного возмущения:
дисперсии случайного возмущения:
- Если 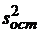 соизмерима с
соизмерима с  , то влияние неадекватности считается незначительным.
, то влияние неадекватности считается незначительным.
- Если 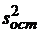 существенно больше
существенно больше  , то модель считается неадекватной.
, то модель считается неадекватной.
Независимая оценка  формируется путем проведения параллельных опытов. В пространстве факторов выбирается одна точка
формируется путем проведения параллельных опытов. В пространстве факторов выбирается одна точка  и для этой точки проводится серия независимых экспериментов, результаты которых используются только для оценки
и для этой точки проводится серия независимых экспериментов, результаты которых используются только для оценки  и не используются для оценки регрессионных коэффициентов. То есть заданы конкретные значения для набора факторов
и не используются для оценки регрессионных коэффициентов. То есть заданы конкретные значения для набора факторов  и не изменяя их, зафиксировав в заданном режиме, проводится
и не изменяя их, зафиксировав в заданном режиме, проводится  дополнительных опытов, в результате которых получены отклики
дополнительных опытов, в результате которых получены отклики 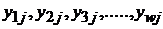 (
( 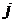 - номер выборки из табл. 1, для которой проводится серия дополнительных экспериментов). В силу того факта, что условия проведения эксперимента остались неизменными, отклики отражают только влияние случайной ошибки. Дисперсия дополнительных опытов и есть
- номер выборки из табл. 1, для которой проводится серия дополнительных экспериментов). В силу того факта, что условия проведения эксперимента остались неизменными, отклики отражают только влияние случайной ошибки. Дисперсия дополнительных опытов и есть  (17).
(17).
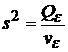 (17)
(17)
где
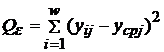 - сумма квадратов нормально распределенных случайных величин;
- сумма квадратов нормально распределенных случайных величин;
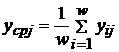 - среднее значение отклика для
- среднее значение отклика для 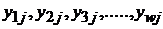 ;
;
 - число степеней свободы;
- число степеней свободы;
 - число дополнительных параллельных экспериментов.
- число дополнительных параллельных экспериментов.
Вводится величина 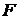 (18) как отношение двух случайных величин, имеющих распределение Фишера с
(18) как отношение двух случайных величин, имеющих распределение Фишера с 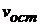 и
и 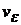 степенями свободы.
степенями свободы.
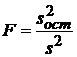 (18)
(18)
С учетом вышеизложенного алгоритм проверки адекватности регрессионной модели сводится к выполнению следующих шагов:
1. Вычисляется по формуле (9) 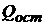 и по формуле (15)
и по формуле (15) 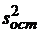 .
.
2. Проводится серия из  дополнительных параллельных экспериментов и по формуле (17) рассчитывается независимая оценка дисперсии случайной ошибки
дополнительных параллельных экспериментов и по формуле (17) рассчитывается независимая оценка дисперсии случайной ошибки  .
.
3. Рассчитывается дисперсионное отношение 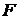 по формуле (18).
по формуле (18).
4. С учетом заданного уровня значимости 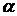 (уровень значимости определяется исследователем) и чисел степеней свободы
(уровень значимости определяется исследователем) и чисел степеней свободы 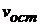 .и
.и 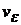 по таблице распределения Фишера получают величину
по таблице распределения Фишера получают величину 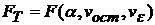 .
.
Распределение Фишера (F-распределение) формируется исходя из двух значений степеней свободы (в учебном пособии не представлены таблицы F-распределения, в силу их значительного объема и свободной доступности). В стандартных таблицах F-распределения введены следующие обозначения для поиска необходимого значения F-распределения:
- 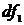 - число степеней свободы большей дисперсии и всегда соответствует числителю.
- число степеней свободы большей дисперсии и всегда соответствует числителю.
- 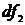 число степеней свободы меньшей дисперсии и соответствует знаменателю.
число степеней свободы меньшей дисперсии и соответствует знаменателю.
- Столбцы таблицы F-распределения соответствуют числителю 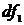 .
.
- Строки таблицы F-распределения соответствуют знаменателю 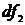 .
.
- Каждая таблица F-распределения соответствует определенному уровню значимости 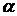 . Для F-распределения составлены таблицы для следующих уровней значимости:
. Для F-распределения составлены таблицы для следующих уровней значимости: 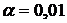 ,
, 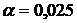 ,
, 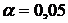 ,
, 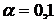 .
.
5. Проводится сравнение величин 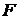 и
и  , на основании которого делаются следующие выводы:
, на основании которого делаются следующие выводы:
- Если 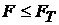 , то регрессионная модель считается адекватной.
, то регрессионная модель считается адекватной.
- Если 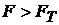 , то регрессионная модель неадекватна.
, то регрессионная модель неадекватна.
Используя данный алгоритм для оценки адекватности регрессионной модели, необходимо учитывать следующие особенности:
1. Уровень значимости 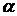 представляет собой вероятность ошибки первого рода, формирующей вероятность того, что модель не адекватна, когда на самом деле она верна. Как правило величина
представляет собой вероятность ошибки первого рода, формирующей вероятность того, что модель не адекватна, когда на самом деле она верна. Как правило величина 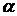 задается исследователем в диапазоне [0,01, 0,1]. На практике исследователи часто используют значение
задается исследователем в диапазоне [0,01, 0,1]. На практике исследователи часто используют значение 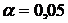 . Таким образом, выбором исследователем значения
. Таким образом, выбором исследователем значения 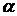 , производится согласие исследователя зависит принимать адекватность модели с большей или меньшей точностью.
, производится согласие исследователя зависит принимать адекватность модели с большей или меньшей точностью.
2. Числа степеней свободы 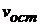 .и
.и 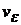 зависят от числа проведенных опытов. Чем меньше проведено опытов, тем менее надежны результаты. Желательно, что бы степени свободы соответствовали как минимум числу 5.
зависят от числа проведенных опытов. Чем меньше проведено опытов, тем менее надежны результаты. Желательно, что бы степени свободы соответствовали как минимум числу 5.
3. Может получиться так, что 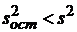 . В данном случае строится обратное соотношение двух случайных величин, имеющих распределение Фишера с
. В данном случае строится обратное соотношение двух случайных величин, имеющих распределение Фишера с 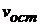 .и
.и 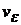 степенями свободы
степенями свободы 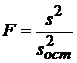 , для которого также по таблице Фишера находится
, для которого также по таблице Фишера находится 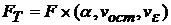 и делаются следующие выводы:
и делаются следующие выводы:
- Если 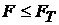 , то регрессионная модель считается адекватной.
, то регрессионная модель считается адекватной.
- Если 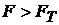 , то требуется тщательное исследование всех возможных ошибок. Причиной получения такого неравенства может быть грубая ошибка в вычислениях, либо неадекватность условий проведения опытов по определению
, то требуется тщательное исследование всех возможных ошибок. Причиной получения такого неравенства может быть грубая ошибка в вычислениях, либо неадекватность условий проведения опытов по определению 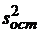 и
и  , либо неоднородность дисперсий отдельных наблюдений.
, либо неоднородность дисперсий отдельных наблюдений.
Если в результате оценки адекватности модели выявлено, что регрессионная модель неадекватна, необходимо изменить ее структуру и заново собрать необходимые данные. Примером, может служить повышение степени полинома регрессионной модели. Однако следует помнить, что повышение степени полинома сверх необходимого не приведет к значительному повышению точности отклика. Включение в модель определенного числа лишних членов затрудняет обработку данных, что обуславливается увеличением числа наблюдений, иначе уменьшается число степеней свободы в процессе проверки адекватности.
