Биномиальное распределение ДСВ

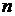Случайная величина , принимающая целые значения от 0 до , имеет биномиальное распределение, если

.

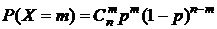Такое распределение имеет случайная величина , равная числу осуществлений некоторого события А в серии из 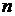испытаний, в каждом из которых вероятность появления события А постоянна и равна 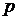. Числовые характеристики биномиального распределения можно найти по формулам:

.

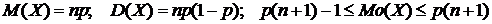Пример. В корзине 50 шаров, из них 10 черных. Достают 5 шаров, причем выборка осуществляется с возвращением. Охарактеризовать случайную величину Х — число обнаруженных в выборке шаров черного цвета.

Величина Х может принимать значения от 0 до 5, т. к. выборка проводится с возвращением, вероятность 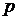обнаружить всякий раз черный шар постоянна и равна 10/50 = 0,2. Вероятности каждого значения вычислим по формуле Бернулли:

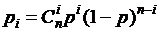, где .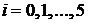

Получим ряд распределения:

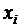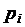	0,32768	0,4096	0,2048	0,0512	0,0064	0,00032

Найдем функцию распределения :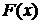

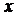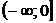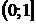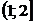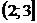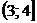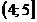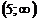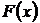		0,32768	0,73728	0,94208	0,99328	0,99968

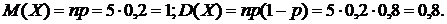
Наивероятнейшее значение ( 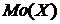) определяется из неравенства

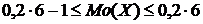или .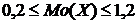

Целым значением, удовлетворяющим этим двум неравенствам, является 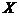= 1. Значит, 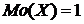, что видно и из ряда распределения.

Гипергеометрическое распределение ДСВ

Случайная величина Х имеет гипергеометрическое распределение, если

.

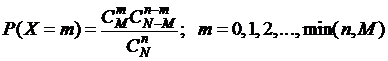Такое распределение получается в следующей задаче. Имеется генеральная совокупность из 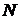объектов, в числе которых находится 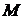интересующих исследователей объектов. Из генеральной совокупности проводится выборка без возвращения объемом 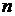. Тогда случайная величина , равная числу интересующих нас объектов из совокупности 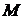, обнаруженных в выборке, имеет гипергеометрическое распределение.

Пример. Воспользуемся условием предыдущей задачи, считая, что выборка осуществляется без возвращения, и найдем закон распределения случайной величины , равной числу черных шаров в выборке.

Случайная величина может также меняться от 0 до 5. Вычислим вероятности каждого значения по формуле:

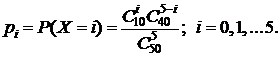
Составим ряд распределения

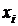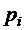	0,310563	0,431337	0,20984	0,044177	0,003965	0,000119

Как видим, вероятности отдельных значений Х несколько изменились по сравнению с их значениями, рассчитанными по формуле Бернулли.

Числовые характеристики гипергеометрического распределения:

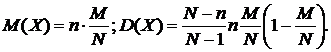
В данном примере .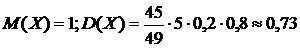

Формулой для математического ожидания можно воспользоваться для оценки размера генеральной совокупности, если непосредственно подсчитать число объектов в ней затруднительно. Такая ситуация возникает, если нужно знать, например, число животных в популяции, обитающей на какой-либо территории, число птиц в стае, рыб в замкнутом водоеме и т. п. В этом случае метят 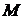объектов из всей совокупности. Через некоторое время отбирают 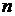объектов и записывают количество меченых. Повторяя отбор несколько раз, находят среднее количество меченых объектов, которое можно принять равным 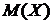. Зная 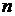, 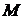и 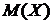можно найти .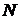