Явный метод расчета ползучести

Модели ползучести, реализуемые в ANSYSс использованием явного метода, задаются константами С₆, С₁₂ и С₆₆ (таблица 1). Расчет первой стадии ползучести (неустановившаяся ползучесть) определяется константой C₆. Если константа С₁≤0 или температурапо шкале Кельвина T≤0, то первая стадия ползучести исключается из расчета. Вторая стадия (установившаяся ползучесть) определяется константой С₁₂, которая может быть равна нулю или единице.Если С₇≤0 или T≤0, то из расчета исключается вторая стадия ползучести. Ползучесть, вызванная радиационным излучением, определяется константой С₆₆. Единственная доступная в пакете ANSYSмодель радиационной ползучести выбирается путем задания С₆₆ = 5. Она может использоваться в сочетании с C₆ от0 до 11. Если С₅₅≤0 или С₆₁≤0 или T≤0, то радиационная ползучесть не рассчитывается.

Таблица 3.1.1

Модель ползучести	Стадия	C6, C12, C66
Деформационное упрочнение		С6 = 0
Временное упрочнение		С6 = 1
Обобщенное экспоненциальное упрочнение		С6 = 2
Нержавеющаясталь (Annealed 304 Stainless Steel)	1, 2	С6 = 9
Нержавеющаясталь (Annealed 316 Stainless Steel)	1, 2	С6 = 10
Нержавеющаясталь (Annealed 2.25Cr /1Mo Steel)	1, 2	С6 = 11
Степенной закон ползучести		С6 = 12
Закон Стерлинга	1, 2	С6 = 13
Нержавеющаясталь (Annealed 316 Stainless Steel)	1, 2	С6 = 14
Полиномиальная модель	1, 2	С6 = 15
Экспоненциальный закон		С12 = 0
Закон Нортона		С12 = 1
Радиационная ползучесть (20% ColdWorked 316 SS)	1, 2	С66 = 5
Закон, заданный пользователем		С6 = 100

Рассмотрим модели, приведенные в таблице 1,более детально:

· Модель деформационного упрочнения

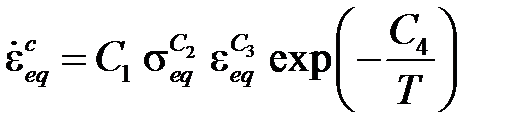
описывает первую стадию ползучести (неустановившаяся ползучесть) и реализуется при C₆= 0. Здесь 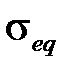– это эквивалентное напряжение по критерию Мизеса, а 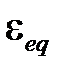– соответствующая эквивалентная деформация

,

.

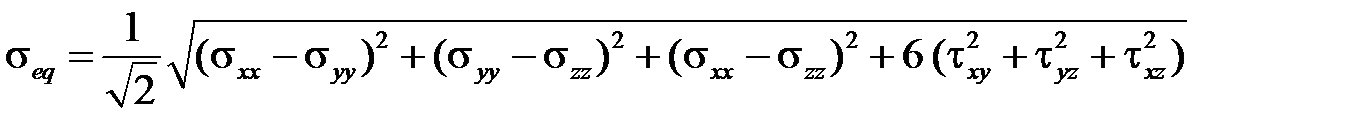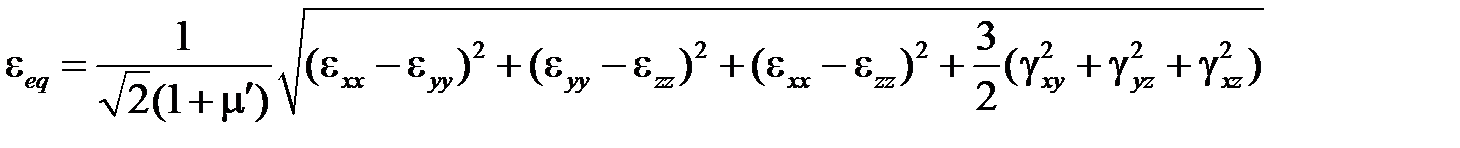Константа 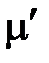в последнем выражении равна:

а) коэффициенту Пуассона μ при расчете упругой и тепловой составляющей деформации;

б) 0,5 для неупругой деформации и деформации ползучести;

в) 0 для одномерных конечных элементов.

· Модель временного упрочнения

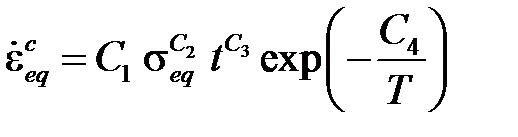
описывает первую стадию ползучести и реализуется при C₆= 1.

· Обобщенная модель экспоненциального упрочнения

,

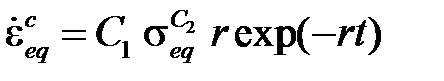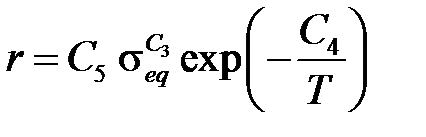
описывает первую стадию ползучести и реализуется при C₆= 2.

· Законы ползучести для сталей

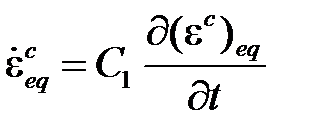
описывает первую и вторую стадию ползучести и реализуется при C₆= 9, 10, 11, 14 ,15. Описание опций для задания деформаций ползучести имеется в главе Elementsmanual 2.5.

· Степенной закон ползучести

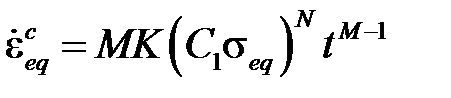
описывает первую стадию ползучести и реализуется при C₆= 12. Описание опций для задания функций M, N, K имеется в главе Elementsmanual 2.5.

· Закон Стерлинга

, , , ,

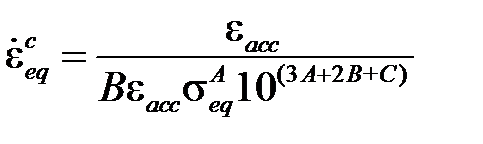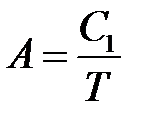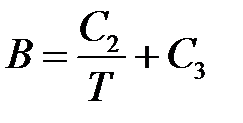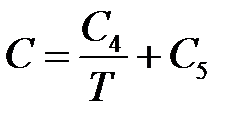где 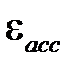– это накопленная деформация ползучести, описывает первую и вторую стадию ползучести и реализуется при C₆= 13, C₁= 0, C₇= 0.

· Экспоненциальный закон

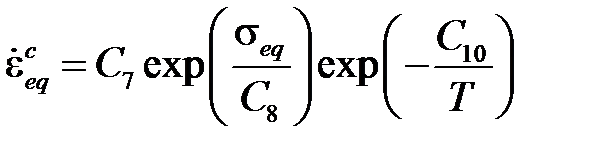
описывает вторую стадию ползучести и реализуется при C₁₂= 0.

· Закон Нортона

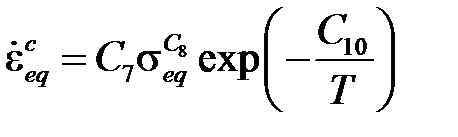
описывает вторую стадию ползучести и реализуется при C₁₂= 1.

Типы элементов, которые поддерживают неявный метод расчета ползучести: PLANE42, SOLID45, PLANE82, SOLID92, SOLID95 и др. Модели пластичности, которые допускается сочетать с моделями ползучести в неявном методе: BISO, MISO, BKIN, KINH/MKIN и др.