Уравнения, вкоторых впоказателестепенипереднеизвестнымстоитодини тотжекоэффициент,решаютсявынесением заскобкуобщегомножителя (чащенаименьшего)

3^{2х – 5} + 3^{2х – 7} + 3^{2х – 9} = 91

3^{2х – 9}(3⁴ + 3² + 1) = 91; 3^{2х – 9} = 1;х = 4,5Ответ: х = 4,5

4)Уравнениявида:a^{f (x)} = b^{f (x)}(a> 0; b> 0; a 1; b 1; a b).Решение: (a/b)^{f (x)} = 1

а) ; Ответ: решенийнет

б)2^{8 – х} + 7^{3 – х} = 7^{4 – х} + 2^{3 – х}

2^{3 – х}(2⁵ – 11) = 7^{3 – х}(7 – 1); (2/7)^{3 – х} = 6/21; 3 – х = 1; х = 2Ответ: х = 2

в)

Ответ: х =

Уравнения,сводящиесякквадратным.

а)

б) ОДЗ:

Ответ: х = 1,5

в)2^3х + 8 - 6 = 0

2^х(2^2х - 6 + 8) = 0; 2^х 0; 2^х = 2; х = 1; 2^х = 4; х = 2Ответ: х = 1; х = 2

г) Ответ: х = 0

Однородныеуравнения.

а)2 - 3 - 5 = 0

(2/5)^2х - (2/5)^х – 5 = 0;Д = 49; (2/5)^х -1; (2/5)^х = 5/2; х = -1Ответ: х = -1

б)10^2/х + 25^1/х = 50^1/х;ОДЗ: х 0

(10/5)^2/х – 17/ (10/5)^1/х + 1 = 0;Д = 225;2^1/х = 4; х = 1/2;2^1/х = 1/4;х = -1/2Ответ:х =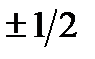

в) ;ОДЗ: х 0

Ответ: х =

7)Уравнениявидаa^{f (x)} = b^{р (x)}(a> 0; b> 0; a 1; b 1; a b)решаютсялогарифмированиемобеихчастейпоодномуоснованию.

а)1 сп.)2^{х – 3} = 3^х

lg2^{х – 3} = lg 3^х; (x – 3)lg2 = xlg3; x = Ответ: х =

2 cп.)2^{х – 3} = 3^х; Ответ: х = (привести к одному показателю)

б)

в)

г)

Нестандартныеспособырешения.

а)2^3х - ;Ответ: х = 1

б) (Разделить на )

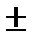Ответ: х = 2

в) - «завуалированное» обратное число

Ответ: х =

г) - использование монотонности

единственный корень уравненияОтвет: х =

д) - использование монотонности

Уравнение имеет не более одного корнях = 1- проверка подтверждает.Ответ: х = 1

е) - использование монотонности

Уравнение имеет не более одного корнях = 1- проверка подтверждает.Ответ: х = 1

ж)

1) х = 0 – левая часть не имеет смысла

2) ;Ответ: х =

з)

1) х = 1 – левая и правая части не имеют смысла

2) Ответ: х = 0; х = 2; х = 4

РЕШЕНИЕПОКАЗАТЕЛЬНЫХНЕРАВЕНСТВ

Методы решения анaлогичны. Обязательно учитывать основание.

1) ;ОДЗ: х - 4;Ответ: х

2) Ответ: х > 2

3)4^х - 5^2х – 10^х> 0

(2/5)^2x – (2/5)^x – 2 > 0; (2/5)^x< -1; (2/5)^x> 2; x<log_2/52Ответ: х <log_2/52

4)7^{х +2}- 7^{х + 1} + 7^х>60

7^х (49-21 + 2) >60; 7^х>60; 7^х>2; Ответ:

5)5^{2x + 1} + 6^{x + 1}> 30 +

5^2x(5 – 6^x) - 6(5 – 6^x) > 0; (5 – 6^x)(5^2x – 6) > 0Ответ: х

6) ; ( )Ответ: х

7) ; ОДЗ: х 0

Ответ: х

8)

Ответ: х =

ОСНОВНЫЕСПОСОБЫРЕШЕНИЯЛОГАРИФМИЧЕСКИХУРАВНЕНИЙ

При использовании формул: слева направо возможно сужение области определения. Следовательно, возможна потеря корней. Такое применение этих формул не рекомендуется.

При использовании этих формул справа налево возможно расширение области определения. Следовательно, возможно появление посторонних корней.Следовательно, необходимо делать проверку или находить ОДЗ.

1)Уравнения, решаемыеспомощьюопределениялогарифма.

а)log₃(x – 12) = 2; ;x = 21;Ответ: х = 21

б)log₁₁log₃log₂ = 0; (ОДЗ:х ) Отв:

Уравнения,решаемыесприменениемсвойствлогарифмов.

а)2lg(x – 1) = 1/2 lgx⁵ - lg ; (ОДЗ:х > 1)(x – 1)² = x²; x = 1/2;Ответ: решенийнет

б)lg(x³ + 1) – 0,5lg(x² + 2x + 1) = lg3; (ОДЗ:х > -1); x² – x – 2 = 0 ; x = -1; x = 2;Ответ: 2

в)log₅x² = 0; (ОДЗ: х 0); 1 сп.)х² = 1; х = ;2 сп.)2lg Ответ:

г) = 2;ОДЗ: x< -5;x> -1Применяем формулу справа налево.

Ответ: -15;5

д) ;ОДЗ:

Ответ:

е)log_kx + log x + …+ log x = ;ОДЗ:х > 0;

log_kx(1+2+3+…+k)= Ответ: х =

ж)Использованиесвойствалогарифмов:

1)х^lg9 + 9^lgx = 6;ОДЗ: х > 0

x^lg9 = 9^lgx = 6; 3^2lgx = 3; lgx = 1/2;Ответ: х =

2) ;ОДЗ:

Ответ:

з-1)

Ответ: если ; если

з-2)

Ответ: если ; если

и)

Ответ: если ; если если

Уравнения c логарифмами разных оснований приводятся к одному основанию.

а) ОДЗ:х > 0; (4log₃x = 6; log₃x = 3/2)Ответ: х = 3

б)log₃x + 2log_x3 = 3;ОДЗ:х > 0; x 1

log₃x = h;h + 2/h = 3;h = 1; x =3; h = 2; x = 9;Ответ: х = 3; x = 9

Уравнения,решаемыевынесениемобщегомножителязаскобку.

log (x – 2)log₅x = 2log₃(x – 2);ОДЗ:х> 2

2log₃(x – 2)(log₅x – 1) = 0; x = 3; x = 5;Ответ: х = 3; x = 5

5)Уравнениявида решаютсяосвобождениемотдроби.

а) ;ОДЗ:х > 2; x 3; + проверка.

х³ – 5х² +19 = (х – 2)³; х = 3; х = 9Ответ: х = 9

б) ;ОДЗ:х > 0; x 10 ^{– 1}; x 10⁵

lg²x – 5lgx + 6 = 0; lgx = 2; x = 100;lgx = 3; x = 1000Ответ: х = 100; x = 1000

6)Уравнениявторой (и более)степениотносительнологарифмарешаютсявведениемновойпеременной. ( logⁿ_ax^k = kⁿlogⁿ_ax )

logx³ – 17log₂x – 2 = 0 ;ОДЗ:х> 0

9 logx – 17log₂x – 2 = 0; log₂x = h; Д = 361 = 19²; h = -1/9;2Ответ: х = 4; x = 2 ^{– 1/ 9}