Разложение в ряд Маклорена некоторых функций

1.

Имеем ;

, и по формуле (5.2) получаем

. (5.3)

Областью сходимости этого степенного ряда является интервал .

2.

Имеем: , , , , , откуда

, , , , и т.д.

Очевидно, что производные четного порядка , а нечетного порядка , , и по формуле (5.2) имеем

(5.4)

Область сходимости ряда .

3. .

Рассматривая аналогично функции , получим:

(5.5)

Область сходимости ряда .

4. , где – любое действительное число.

Имеем , ,

, , …,

, …

При : , , ,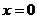

, …, и по формуле (5.2) получаем

(5.6)

Найдем интервал сходимости ряда:

Ряд, составленный из модулей , исследуем с помощью признака Даламбера:

.

Следовательно, интервал сходимости ряда . На концах интервала при сходимость ряда зависит от конкретных значений .

Ряд (5.6) называется биномиальным. Если – целое положительное число, то биномиальный ряд представляет формулу бинома Ньютона, так как при сомножитель равен нулю, следовательно, 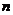-йчлен ряда и все последующие равны нулю, т.е. ряд обрывается, и вместо бесконечного разложения получается конечная сумма.

Выпишем некоторые разложения функции при различных .

:

, (5.7)

Если в это разложение подставить вместо 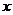, получим:

(5.8)

:

, (5.9)

:

, (5.10)

5. .

Получить разложение для этой функции, непосредственно вычисляя коэффициенты с помощью производных, не очень просто, поэтому мы воспользуемся разложением (5.7) и свойством 2) степенных рядов. Интегрируя почленно равенство (5.7) в интервале , где , с учетом того, что , получим

(5.11)

Область сходимости ряда (после выяснения сходимости на концах интервала) есть .

6.

Проделаем то же самое, что и в предыдущем случае, воспользовавшись разложением (5.8):

(5.12)

Область сходимости ряда .

7.

Воспользуемся разложением (5.10), подставив в него вместо :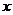

Интегрируя в интервале , где , получаем:

(5.13)

Область сходимости ряда

Можно доказать, что ряды, приведенные в формулах (5.3) – (5.13), сходятся к функциям, для которых они составлены.

При разложении более сложных функций часто используют готовые разложения (5.3) – (5.13).

Примеры

1) Разложить в ряд Маклорена функцию

Решение. Воспользуемся известной тригонометрической формулой

Разложим в ряд Маклорена функцию , заменяя в разложении (5.5) 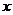на :

Тогда

Это и есть разложение в ряд Маклорена функции . Очевидно, что оно справедливо при любом .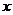

2) Разложить в ряд Тейлора по степеням функцию

Решение. Преобразуем данную функцию так, чтобы можно было воспользоваться разложением (5.7):

Полученное разложение справедливо, когда . Отсюда получаем или .

Применение рядов в приближенных вычислениях

Степенные ряды имеют самые разнообразные приложения. С их помощью вычисляют с заданной степенью точности значения функций, определенных интегралов, которые являются «не берущимися» или слишком сложными для вычислений, интегрируются дифференциальные уравнения.

Примеры

I. Вычислить приближенно с точностью до 0,0001:

а)

Решение. Для вычисления запишем ряд (5.3) при , принадлежащем области сходимости :

Взяв первые пять членов разложения, на основании следствия из теоремы Лейбница для сходящегося знакочередующегося ряда, мы допустим погрешность , не превышающую первого отброшенного члена (по абсолютной величине), т.е. .

Итак,

б)

Решение. Воспользуемся разложением (5.11), подставив в него , входящее в область сходимости :

Так как данный числовой ряд не является знакопеременным, то о погрешности нельзя судить по величине первого отбрасываемого члена.

Если в качестве взять сумму первых трех членов, мы допустим погрешность

(здесь мы учли, что сумма сходящегося геометрического ряда в скобках равна )

Итак,

в)

Решение. Для вычисления запишем ряд (5.4) при , принадлежащем области сходимости :

(необходимо взять два члена, так как при этом погрешность ). Итак,

.

II. Вычислить приближенно с точностью до 0,001 следующие интегралы:

a)

Решение. Так как интеграл «не берущийся», «точное» интегрирование здесь невозможно.

Воспользуемся разложением (5.4). Разделив обе части на 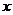, получим

, причем ряд сходится при всех значениях 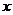. Интегрируя почленно, получим:

Возьмем первые три члена разложения, т.к. .

Итак,

б)

Решение. Заменив 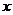на в разложении (5.3), получим:

.

Умножая полученный ряд на :

,

и почленно интегрируя в интервале , принадлежащем интервалу сходимости ряда , имеем:

При этом . Итак, .

Задачи

Разложить в ряд Маклорена следующие функции, указав промежутки сходимости полученных рядов.

86. 87. 88.

89. 90. 91.

92.

Разложить в ряд Тейлора следующие функции и найти область сходимости полученного ряда.

93. по степеням

94 по степеням

95. по степеням

96. по степеням

97. по степеням

98. по степеням

Вычислить приближенно с точностью до 0,0001:

99. 100. 101. 102. 103.

104.

Вычислить приближенно, взяв первые два члена разложения в ряд подынтегральной функции, и оценить допущенные при этом погрешности:

105. 106.

Ответы

В задачах1, 3, 6, 7, 8, 9, 10, 12, 13, 15, 17, 18, 19, 21, 22, 23, 31, 32, 33, 34, 35, 37, 38, 42, 43, 44 – ряды сходятся.

В задачах 2, 4, 5, 11, 14, 16, 20, 24, 25, 26, 27, 28, 29, 30, 36, 39, 40, и 41 – ряды расходятся.

В задачах 45, 46, 47, 49, 50, 51, 55 – ряды абсолютно сходятся.

В задачах 48, 53, 54, 57 – ряды сходятся условно.

В задачах 52, 56, 58, 59 – ряды расходятся.

60.(-1;1],61.[-1/2;1/2),62.{0},63.(-1/3;1/3],64.(-1;1),65.[0;2],66.[-10;10),67.(-∞;∞), 68.(-7;-1), 69. [-4;4), 70. (-2;2), 71. , 72. [1;3), 73. (-1/3;1/3), 74. (-∞;∞), 75. [-1;1], 76. [-1;1), 77. (1;5], 78. (-1/4;1/4), 79. (-1/3;1/3), 80. (-3;1], 81. (-1;1], 82. (-∞;∞), 83. , 84. , 85. [-1/e;1/e),

86. 87.

88. 89.

90. 91.

92. 93.

94. 95.

96. 97.

98.

99. 100. 101.

102. 103. 104.

105. 106. .

Оглавление

§1. Основные понятия. 4

§2. Признаки сходимости знакопостоянных рядов. 7

§3. Признаки сходимости знакопеременных рядов. 22

§4. Степенные ряды.. 27

§5. Ряды Маклорена и Тейлора. 32

§6. Применение рядов в приближенных вычислениях. 39

Ответы.. 43

Подписано в печать 2012 г. Формат 60´84/16. Бумага писчая. Отпечатано на ризографе. Уч. изд. листов 2.
Тираж 600. Заказ №

Московский государственный университет тонких химических технологий им. М.В.Ломоносова

Издательско-полиграфический центр

117571, Москва, просп. Вернадского, 86.

* Напомним, что степенью степенного выражения называется наибольшая из степеней входящих в него слагаемых, само это слагаемое называется старшим, а его коэффициент называется старшим коэффициентом. Например, у степенного выражения старшее слагаемое имеет степень 1,5, а старший коэффициент равен 5.