Признаки сходимости знакопеременных рядов
Определение. Знакочередующимся рядом называется ряд вида
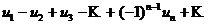 , (3.1)
, (3.1)
где 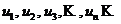 – положительные числа.
– положительные числа.
Для знакочередующихся рядов имеет место следующий достаточный признак сходимости:
Теорема Лейбница. Если члены знакочередующегося ряда (4.1) убывают по абсолютной величине и предел его общего члена при 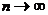 равен нулю, то ряд сходится, а его сумма не превосходит первого члена
равен нулю, то ряд сходится, а его сумма не превосходит первого члена 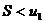 .
.
Т.е. для того, чтобы исследовать знакочередующийся ряд на сходимость, достаточно проверить выполнение двух условий:
1) 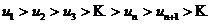 (3.2)
(3.2)
2) 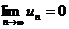 (3.3)
(3.3)
Замечание. Неравенства (3.2) могут выполняться, начиная с некоторого 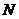 .
.
Примеры
Исследовать на сходимость следующие ряды:
1) 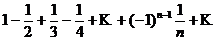
Решение. Т.к. члены данного ряда по абсолютной величине монотонно убывают: 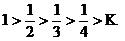 , и вообще,
, и вообще, 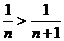 , а общий член ряда при
, а общий член ряда при 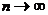 стремится к нулю, то в силу признака Лейбница ряд сходится.
стремится к нулю, то в силу признака Лейбница ряд сходится.
2) 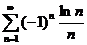 .
.
Решение. Проверим условие (3.2): 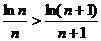 . Доказать это неравенство достаточно сложно. Поэтому применим следующий прием: докажем, что функция
. Доказать это неравенство достаточно сложно. Поэтому применим следующий прием: докажем, что функция 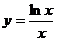 монотонно убывает на некотором интервале вида
монотонно убывает на некотором интервале вида 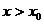 с помощью вычисления производной и исследования функции (это уже было сделано в §2, раздел IV, пример 2). В нашем случае
с помощью вычисления производной и исследования функции (это уже было сделано в §2, раздел IV, пример 2). В нашем случае 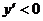 при
при 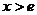 , и функция монотонно убывает в данном промежутке. Следовательно, неравенства (3.2) выполняются для любых
, и функция монотонно убывает в данном промежутке. Следовательно, неравенства (3.2) выполняются для любых 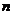 , начиная с трех.
, начиная с трех.
Проверим условие (3.3). Для этого необходимо вычислить 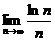 . Используя правило Лопиталя, получим
. Используя правило Лопиталя, получим 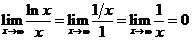 . Следовательно, и
. Следовательно, и 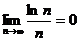 .
.
Т.о., оба условия теоремы Лейбница выполняются, и, следовательно, данный ряд сходится.
Определение. Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.
Очевидно, знакочередующиеся ряды являются частным случаем знакопеременных.
Предполагаем теперь, что в записи
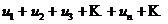 (3.4)
(3.4)
имеются как положительные, так и отрицательные 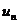 .
.
Теорема. (Модульный признак сходимости знакопеременных рядов).
Если ряд, составленный из абсолютных величин членов данного знакопеременного ряда (3.4):
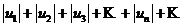 (3.5)
(3.5)
сходится, то сходится и данный ряд.
Отметим, что если ряд (3.5) расходится, то отсюда не следует, что ряд (3.4) будет также расходящимся. Например, ряд 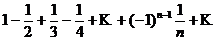 сходится по признаку Лейбница, а ряд из абсолютных величин его членов (гармонический ряд)
сходится по признаку Лейбница, а ряд из абсолютных величин его членов (гармонический ряд) 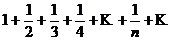 расходится.
расходится.
В связи с этим можно ввести понятие абсолютной и условной сходимости:
Определение. Знакопеременный ряд 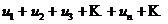 называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов
называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов 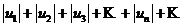 .
.
Определение. Знакопеременный ряд 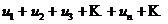 называется условно сходящимся, если ряд, составленный из абсолютных величин
называется условно сходящимся, если ряд, составленный из абсолютных величин 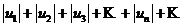 , расходится, а сам ряд сходится.
, расходится, а сам ряд сходится.
Например, ряд 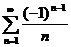 является условно сходящимся (см. пример 1). А ряд
является условно сходящимся (см. пример 1). А ряд 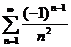 является абсолютно сходящимся, т.к. ряд, составленный из абсолютных величин
является абсолютно сходящимся, т.к. ряд, составленный из абсолютных величин 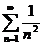 , сходится (обобщенный гармонический при
, сходится (обобщенный гармонический при 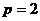 ).
).
Грубо говоря, различие между абсолютно и условно сходящимися рядами заключается в следующем: абсолютно сходящиеся ряды сходятся в основном в силу того, что их члены быстро убывают, а условно сходящиеся – в результате того, что положительные и отрицательные слагаемые частично уничтожают друг друга.
Свойства абсолютно и условно сходящихся рядов существенно различаются: абсолютно сходящиеся ряды по своим свойствам напоминают конечные суммы: их можно складывать, перемножать, переставлять местами члены ряда. Условно сходящиеся ряды такими свойствами не обладают. Возьмем, например, условно сходящийся ряд 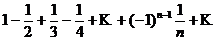 . Переставим члены ряда местами и сгруппируем их следующим образом:
. Переставим члены ряда местами и сгруппируем их следующим образом:
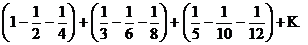
Перепишем ряд в виде (произведя первое действие в каждой скобке):
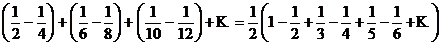
Видим, что от перестановки членов ряда сумма его уменьшилась в 2 раза.
Можно показать (теорема Римана), что от перестановки членов условно сходящегося ряда можно получить ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд.
Примеры
Исследовать ряды на абсолютную и условную сходимость.
1) 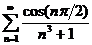
Решение. Ряд, составленный из абсолютных величин членов данного ряда: 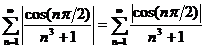 сходится по признаку сравнения, т.к.
сходится по признаку сравнения, т.к. 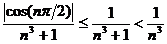 , а ряд
, а ряд 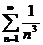 – сходится (обобщенный гармонический ряд при
– сходится (обобщенный гармонический ряд при 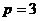 ). Следовательно, данный ряд является абсолютно сходящимся.
). Следовательно, данный ряд является абсолютно сходящимся.
2) 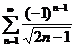
Решение. Составим ряд из абсолютных величин членов данного ряда: 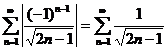 . Исследуем этот ряд на сходимость с помощью предельного признака сравнения, сравнив его с эталонным рядом
. Исследуем этот ряд на сходимость с помощью предельного признака сравнения, сравнив его с эталонным рядом 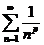 (p подберем в процессе сравнения), имеем
(p подберем в процессе сравнения), имеем 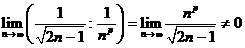 и
и 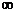 лишь при равенстве степеней числителя и знаменателя, т.е. при
лишь при равенстве степеней числителя и знаменателя, т.е. при 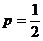 , следовательно, сравниваемые ряды являются расходящимися. Таким образом, ряд, составленный из модулей, расходится, и абсолютной сходимости нет.
, следовательно, сравниваемые ряды являются расходящимися. Таким образом, ряд, составленный из модулей, расходится, и абсолютной сходимости нет.
Исследуем данный знакочередующийся ряд с помощью признака Лейбница. Очевидно, что:
1) 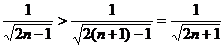 , 2)
, 2) 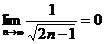 .
.
Оба пункта признака Лейбница выполнены, следовательно, данный ряд условно сходится.
Задачи
Исследовать ряды на абсолютную и условную сходимость:
45. 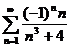 46.
46. 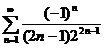 47.
47. 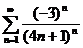
48. 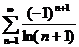 49.
49. 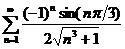 50.
50. 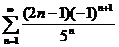
51. 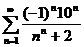 52.
52. 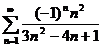 53.
53. 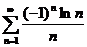
54. 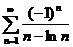 55.
55. 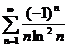 56.
56. 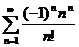
57. 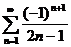 58.
58. 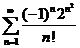 59.
59. 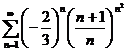
Степенные ряды
До сих пор мы рассматривали ряды, членами которых были числа, т.е. числовые ряды. Перейдем к рассмотрению рядов, членами которых являются функции, в частности, степенные функции с целыми неотрицательными показателями степени:
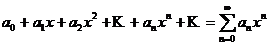 (4.1)
(4.1)
Определение. Ряд вида (4.1) называется степенным, а числа 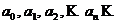 называются коэффициентами степенного ряда.
называются коэффициентами степенного ряда.
Рассматривают и степенные ряды более общего вида:
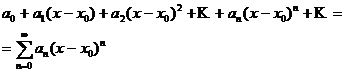 (4.2)
(4.2)
(по степеням 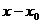 ). Такой ряд не отличается существенно от ряда вида (4.1), ибо приводится к нему простой заменой переменной:
). Такой ряд не отличается существенно от ряда вида (4.1), ибо приводится к нему простой заменой переменной: 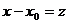 .
.
Определение. Множество значений 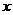 , при которых степенной ряд (4.1) или (4.2) сходится, называется областью сходимости степенного ряда.
, при которых степенной ряд (4.1) или (4.2) сходится, называется областью сходимости степенного ряда.
Структура области сходимости степенного ряда устанавливается с помощью следующей теоремы:
Теорема Абеля
1) Если степенной ряд вида (4.1), т.е. по степеням 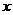 , сходится при значении
, сходится при значении 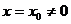 (отличном от нуля), то он сходится, и притом абсолютно, при всех значениях
(отличном от нуля), то он сходится, и притом абсолютно, при всех значениях 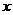 таких, что
таких, что 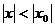 .
.
2) Если степенной ряд вида (4.1) расходится при значении 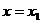 , то он расходится при всех значениях
, то он расходится при всех значениях 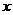 таких, что
таких, что 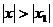 .
.
Из теоремы Абеля вытекает следующая теорема.
Теорема. Областью сходимости степенного ряда вида (4.2), т.е. ряда по степеням 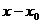 , является интервал с центром в точке
, является интервал с центром в точке 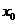 и с концами в точках
и с концами в точках 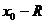 и
и 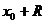 .
.
Число 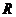 получило название радиуса сходимости, а интервал
получило название радиуса сходимости, а интервал 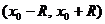 – интервала сходимости степенного ряда. На концах интервала сходимости, т.е. при
– интервала сходимости степенного ряда. На концах интервала сходимости, т.е. при 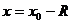 и
и 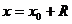 вопрос о сходимости или расходимости данного ряда решается индивидуально для каждого конкретного ряда.
вопрос о сходимости или расходимости данного ряда решается индивидуально для каждого конкретного ряда.
У некоторых рядов интервал сходимости вырождается в точку 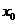 (при
(при 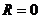 ), у других охватывает всю числовую ось (при
), у других охватывает всю числовую ось (при 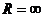 ).
).
Для начала укажем способ определения интервала сходимости степенного ряда на примере ряда (4.1).
Рассмотрим ряд, составленный из абсолютных величин членов этого ряда:
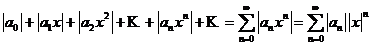 (4.3)
(4.3)
Т.к. при каждом конкретном 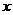 ряд (4.3) является числовым знакоположительным рядом, то для выяснения вопроса о его сходимости можно воспользоваться признаком Даламбера:
ряд (4.3) является числовым знакоположительным рядом, то для выяснения вопроса о его сходимости можно воспользоваться признаком Даламбера:
Допустим, что существует
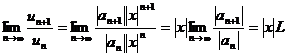 .
.
Тогда, по признаку Даламбера ряд сходится, если 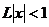 (т.е. при
(т.е. при 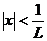 ), и расходится, если
), и расходится, если 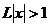 (т.е. при
(т.е. при 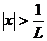 ).
).
Следовательно, ряд (4.1) сходится абсолютно при 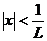 и расходится при
и расходится при 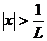 , и интервалом сходимости является интервал
, и интервалом сходимости является интервал 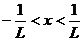 , а радиусом сходимости является число
, а радиусом сходимости является число 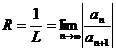 .
.
При 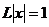 признак Даламбера не дает ответа на вопрос о сходимости, поэтому необходимо, подставляя значения
признак Даламбера не дает ответа на вопрос о сходимости, поэтому необходимо, подставляя значения 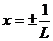 в ряд (4.1), исследовать получающиеся числовые ряды в каждом конкретном случае.
в ряд (4.1), исследовать получающиеся числовые ряды в каждом конкретном случае.
Замечание. Интервал сходимости можно найти, используя радикальный признак Коши (также применяя его к ряду (4.3)):
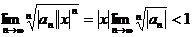
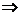
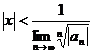 .
.
Примеры
Найти области сходимости степенных рядов:
1) 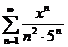
Решение. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда
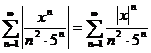 .
.
Применим к нему признак Даламбера.
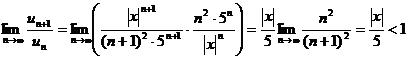
Отсюда получаем интервал сходимости: 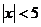 .
.
Исследуем сходимость на концах интервала:
При 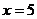 исходный ряд принимает вид:
исходный ряд принимает вид: 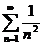 – это обобщенный гармонический ряд при
– это обобщенный гармонический ряд при 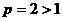 , а значит, он сходится. При
, а значит, он сходится. При 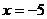 получаем абсолютно сходящийся ряд
получаем абсолютно сходящийся ряд 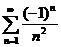 , т.к. ряд, составленный из модулей его членов, сходится.
, т.к. ряд, составленный из модулей его членов, сходится.
Следовательно, интервал сходимости ряда имеет вид: 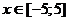 .
.
2) 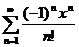 .
.
Решение. Ряд, составленный из модулей, имеет вид:
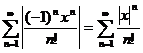 .
.
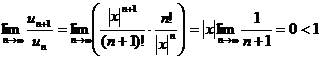
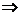 ряд сходится при любых
ряд сходится при любых 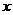 . Таким образом, интервалом сходимости является интервал
. Таким образом, интервалом сходимости является интервал 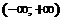 .
.
3) 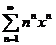
Решение. Ряд, составленный из абсолютных величин членов данного ряда 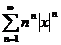 , исследуем с помощью радикального признака Коши:
, исследуем с помощью радикального признака Коши: 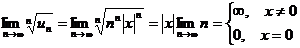
Следовательно, область сходимости ряда состоит из одной точки 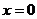 .
.
4) 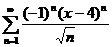
Решение
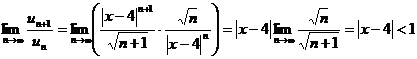 .
.
Отсюда получаем интервал сходимости: 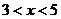 .
.
При 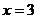 исходный ряд имеет вид:
исходный ряд имеет вид: 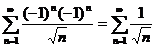 – это расходящийся ряд (обобщенный гармонический при
– это расходящийся ряд (обобщенный гармонический при 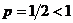 ). Подставляя
). Подставляя 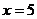 , получаем условно сходящийся ряд
, получаем условно сходящийся ряд 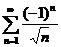 . Окончательно, интервал сходимости ряда имеет вид:
. Окончательно, интервал сходимости ряда имеет вид: 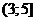 .
.
Свойства степенных рядов
1. Сумма степенного ряда 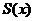 является непрерывной функцией во всем интервале сходимости ряда.
является непрерывной функцией во всем интервале сходимости ряда.
2. Степенной ряд можно почленно интегрировать по любому отрезку 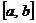 , лежащему в интервале сходимости
, лежащему в интервале сходимости
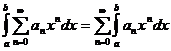 .
.
3. Степенной ряд внутри интервала сходимости можно почленно дифференцировать сколь угодно раз. При этом будут получаться степенные ряды с тем же радиусом сходимости:
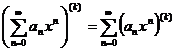
Задачи. Найти области сходимости степенных рядов:
60 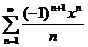 61.
61. 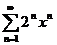 62.
62. 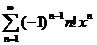
63. 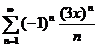 64.
64. 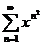 65.
65. 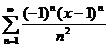
66. 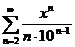 67.
67. 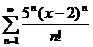 68.
68. 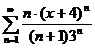
69. 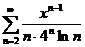 70.
70. 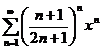 71.
71. 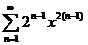
72. 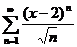 73.
73. 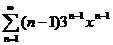 74.
74. 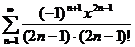
75. 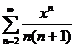 76.
76. 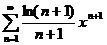 77.
77. 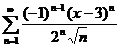
78. 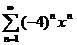 79.
79. 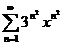 80.
80. 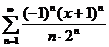
81. 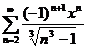 82.
82. 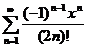 83.
83. 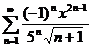
84. 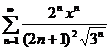 85.
85. 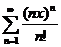 (Указание: при исследовании сходимости на правом конце интервала учесть, что факториалы больших чисел могут быть выражены приближенно формулой Стирлинга
(Указание: при исследовании сходимости на правом конце интервала учесть, что факториалы больших чисел могут быть выражены приближенно формулой Стирлинга 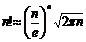 ).
).
Ряды Маклорена и Тейлора
Предположим, что функция 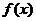 , определенная и бесконечно дифференцируемая в окрестности точки
, определенная и бесконечно дифференцируемая в окрестности точки 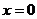 , может быть представлена в виде суммы степенного ряда или, другими словами, может быть разложена в степенной ряд
, может быть представлена в виде суммы степенного ряда или, другими словами, может быть разложена в степенной ряд
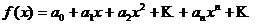 (5.1)
(5.1)
Выразим коэффициенты ряда через 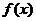 . Найдем производные функции
. Найдем производные функции 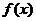 , почленно дифференцируя ряд
, почленно дифференцируя ряд 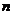 раз:
раз:
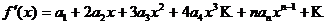
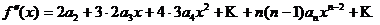
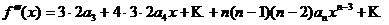
…………………………………………………………….
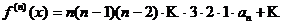
Полагая в полученных равенствах 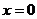 , получим
, получим 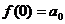 ,
, 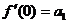 ,
, 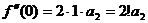 ,
, 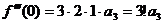 , …,
, …, 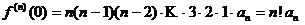 , откуда
, откуда
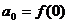 ,
, 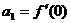 ,
, 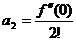 ,
, 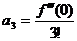 ,…,
,…, 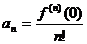 ,…
,…
Подставляя значения коэффициентов 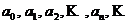 , в (5.1), получим ряд:
, в (5.1), получим ряд:
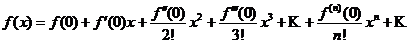 (5.2)
(5.2)
называемый рядом Маклорена.
Отметим, что не все функции могут быть разложены в ряд Маклорена. Может оказаться, что ряд Маклорена, составленный формально для функции 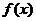 , является расходящимся или сходящимся не к функции
, является расходящимся или сходящимся не к функции 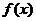 .
.
Если представить ряд Маклорена в виде 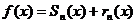 , где
, где 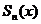 –
– 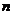 -я частичная суммаряда,
-я частичная суммаряда, 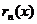 –
– 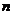 -й остаток ряда, то можно сформулировать следующую теорему:
-й остаток ряда, то можно сформулировать следующую теорему:
Теорема. Для того чтобы ряд Маклорена сходился к функции 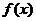 , необходимо и достаточно, чтобы при
, необходимо и достаточно, чтобы при 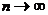 остаток ряда стремился к нулю, т.е.
остаток ряда стремился к нулю, т.е. 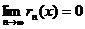 для всех значений
для всех значений 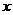 из интервала сходимости ряда.
из интервала сходимости ряда.
Можно доказать, что если функция 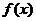 разложима в ряд Маклорена, то это разложение единственное.
разложима в ряд Маклорена, то это разложение единственное.
Замечание. Ряд Маклорена является частным случаем ряда Тейлора:
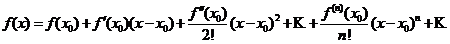 при
при 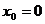
Ряд Тейлора тесно связан с формулой Тейлора:
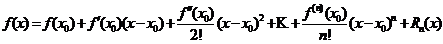 , где
, где 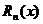 – остаточный член формулы Тейлора, который можно записать в форме Лагранжа:
– остаточный член формулы Тейлора, который можно записать в форме Лагранжа:
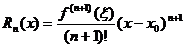 ,
, 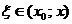 .
.
