Признаки сходимости знакопостоянных рядов
Ряды
Учебно-методическое пособие
Москва 2012
УДК 51
ББК 22.1
Рецензент – доктор физ.-мат.наук, профессор Карташов Э.М.
Л.М. Ожерелкова, А.Г. Рубин, И.А. Джемесюк
Ряды. Учебно-методическое пособие. М.: ИПЦ МИТХТ, 44 с.
Утверждено библиотечно-издательской комиссией
в качестве учебно-методического пособия
для студентов 2–4-го курсов дневного отделения
всех специальностей МИТХТ им. М.В.Ломоносова
по дисциплине «Высшая математика», поз. /2012.
МИТХТ им. М.В.Ломоносова, 2012
Основные понятия
Определение. Числовым рядом называется бесконечная последовательность чисел 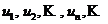 , соединенных знаком сложения:
, соединенных знаком сложения:
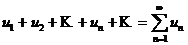 . (1.1)
. (1.1)
Числа 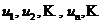 называются членами ряда, а член
называются членами ряда, а член 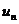 – общим или n-м членом ряда.
– общим или n-м членом ряда.
Ряд (1.1) считается заданным, если известен его общий член 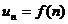 , (
, ( 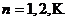 ), т.е. задана функция
), т.е. задана функция 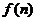 натурального аргумента. Например, ряд с общим членом
натурального аргумента. Например, ряд с общим членом 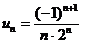 имеет вид:
имеет вид: 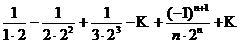
Образуем новую последовательность:
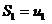
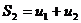
………………..
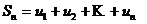
Определение. Сумма 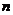 первых членов ряда называется n-ой частичной суммой ряда и обозначается
первых членов ряда называется n-ой частичной суммой ряда и обозначается 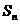 .
.
Определение. Если последовательность частичных сумм ряда имеет предел, то такой ряд называется сходящимся, а этот предел называется суммой ряда.
То есть, если 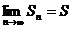 , то ряд сходится, а
, то ряд сходится, а 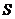 – сумма ряда. В этом смысле можно записать
– сумма ряда. В этом смысле можно записать 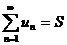 .
.
Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся. У расходящегося ряда суммы нет.
Пример 1. Исследовать на сходимость геометрический ряд, т.е. ряд, составленный из последовательных членов геометрической прогрессии:
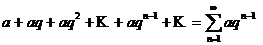 (1.2)
(1.2)
Решение. Необходимо установить, при каких значениях знаменателя прогрессии  ряд (1.2) сходится, а при каких – расходится. Из школьного курса алгебры известно, что сумма первых
ряд (1.2) сходится, а при каких – расходится. Из школьного курса алгебры известно, что сумма первых  членов геометрической прогрессии, т.е. n-я частичная сумма ряда при
членов геометрической прогрессии, т.е. n-я частичная сумма ряда при 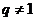 равна
равна 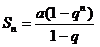 .
.
Возможно несколько случаев:
1) если 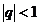 , то
, то 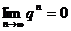
и 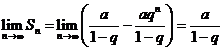 , т.е. ряд сходится и его сумма
, т.е. ряд сходится и его сумма 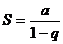 .
.
2) если 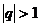 , то
, то 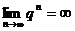 и, следовательно,
и, следовательно, 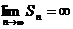 , и ряд расходится.
, и ряд расходится.
3) если 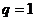 , то ряд (1.2) примет вид
, то ряд (1.2) примет вид 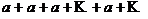 , его
, его 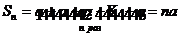 и
и 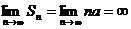 ,
, 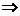 ряд расходится.
ряд расходится.
4) если 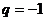 , то ряд (1.2) примет вид
, то ряд (1.2) примет вид 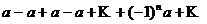 , и его
, и его 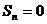 при
при 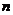 четном и
четном и 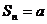 при
при 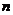 нечетном, следовательно,
нечетном, следовательно, 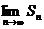 не существует, и ряд расходится.
не существует, и ряд расходится.
Т.о. геометрический ряд сходится к сумме 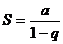 при
при 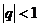 и расходится при
и расходится при 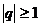 .
.
Пример 2. Найти сумму ряда:
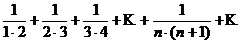
Решение. 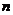 -я частичная сумма ряда:
-я частичная сумма ряда:
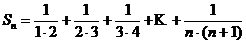
Учитывая, что
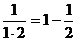 ,
, 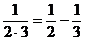 ,
, 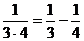 ,...,
,..., 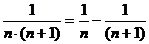 ,
,
частичную сумму ряда можно представить в виде
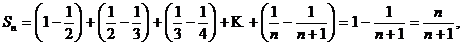 и тогда получаем:
и тогда получаем: 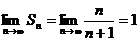 , т.е. сумма ряда
, т.е. сумма ряда 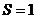 .
.
Свойства сходящихся рядов
Свойство 1. Если ряд 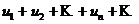 сходится и имеет сумму
сходится и имеет сумму 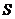 , то и ряд
, то и ряд 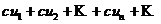 , полученный умножением данного ряда на число
, полученный умножением данного ряда на число 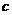 , также сходится, и имеет сумму
, также сходится, и имеет сумму 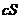 .
.
Свойство 2. Если ряды 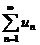 и
и 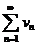 сходятся и их суммы соответственно равны
сходятся и их суммы соответственно равны 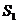 и
и 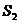 , то и ряды
, то и ряды 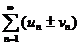 также сходятся и их суммы равны соответственно
также сходятся и их суммы равны соответственно 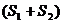 и
и 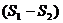 .
.
Свойство 3. Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или добавления) конечного числа членов.
Установить сходимость (расходимость) ряда путем нахождения частичной суммы 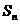 и вычисления
и вычисления 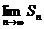 , как это сделано в примерах 1 и 2, возможно лишь в редчайших случаях из-за принципиальных трудностей при нахождении
, как это сделано в примерах 1 и 2, возможно лишь в редчайших случаях из-за принципиальных трудностей при нахождении 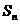 (суммировании первых
(суммировании первых 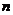 членов ряда). Обычно сходимость (расходимость) ряда устанавливается с помощью специальных теорем – признаков сходимости.
членов ряда). Обычно сходимость (расходимость) ряда устанавливается с помощью специальных теорем – признаков сходимости.
В большинстве признаков сходимости вам придется вычислять некоторый предел. Напомним кратко два основных приема вычисления пределов, которыми вы будете пользоваться чаще всего.
А) Предел отношения двух степенных выражений на бесконечности равен:
0, если степень числителя меньше степени знаменателя;
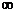 , если степень числителя больше степени знаменателя;
, если степень числителя больше степени знаменателя;
отношению старших коэффициентов, если степень числителя равна степени знаменателя*.
Б) Правило Лопиталя. Предел отношения двух бесконечно малых величин (б.м.) или двух бесконечно больших величин (б.б.) равен пределу отношения их производных. Например, по правилу Лопиталя имеем:
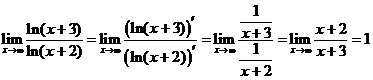
II. Признак Даламбера
Теорема. Пусть для ряда 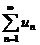 (
( 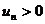 ) существует предел отношения (
) существует предел отношения ( 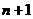 )-го члена ряда к
)-го члена ряда к 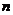 -му:
-му: 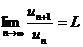 . Тогда:
. Тогда:
а) если 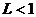 , то ряд сходится,
, то ряд сходится,
б) если 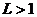 , то ряд расходится,
, то ряд расходится,
в) если 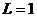 , то вопрос о сходимости ряда остается нерешенным, т. е. признак не работает.
, то вопрос о сходимости ряда остается нерешенным, т. е. признак не работает.
Примеры
Исследовать следующие ряды на сходимость:
1) 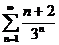 . Решение. Т.к.
. Решение. Т.к.
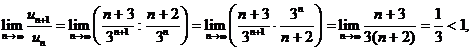 то по признаку Даламбера ряд сходится.
то по признаку Даламбера ряд сходится.
2) 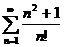
Замечание. Напомним, что 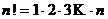 , поэтому
, поэтому 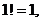
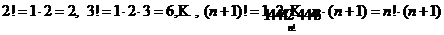 .
.
Решение. Воспользуемся формулой 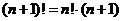 , тогда:
, тогда:
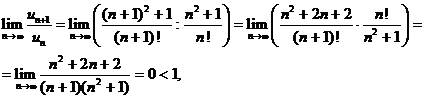
следовательно, по признаку Даламбера ряд сходится.
3) 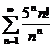
Решение 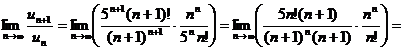
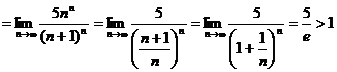
и ряд расходится.
Замечание. С помощью признака Даламбера исследовать ряды на сходимость имеет смысл только тогда, когда в выражении для 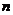 - го члена ряда имеются показательная функция и/или факториал.
- го члена ряда имеются показательная функция и/или факториал.
Примеры
1) Применим интегральный признак к исследованию на сходимость ряда вида 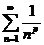 ,
, 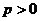 , называемого обобщенным гармоническим рядом или рядом Дирихле.
, называемого обобщенным гармоническим рядом или рядом Дирихле.
Решение. В этом случае требуемой функцией является 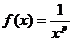 . Функция
. Функция 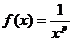 является невозрастающей на интервале
является невозрастающей на интервале 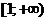 . Вычислим
. Вычислим 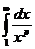 .
.
Если 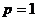 , то
, то 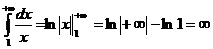 .
.
Если 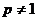 , то
, то 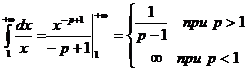 .
.
Следовательно, несобственный интеграл сходится при 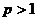 и расходится при
и расходится при 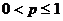 . То же самое можно сказать и о данном ряде.
. То же самое можно сказать и о данном ряде.
Запомнить! Обобщенный гармонический ряд 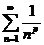 сходитсяпри
сходитсяпри 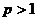 и расходится при
и расходится при 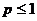 .
.
2) Исследовать на сходимость ряд 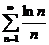 .
.
Решение. Выписав 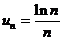 и заменив в нем n на x, получим функцию
и заменив в нем n на x, получим функцию 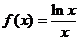 .
.
Внимание! Пока мы не убедились, что функция невозрастающая на некотором интервале вида 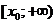 , к интегрированию переходить рано!
, к интегрированию переходить рано!
Исследуем функцию 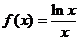 на монотонность с помощью производной:
на монотонность с помощью производной: 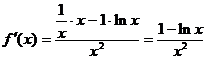 . Критическая точка
. Критическая точка 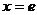 , на интервале
, на интервале 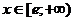
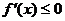 , т.е. функция
, т.е. функция 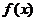 невозрастающая. Теперь можно переходить к интегрированию.
невозрастающая. Теперь можно переходить к интегрированию.
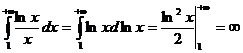 ,
, 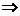 интеграл расходится, расходится и данный ряд.
интеграл расходится, расходится и данный ряд.
V. Признаки сравнения
Теорема.Первый признак сравнения (признак сравнения в форме неравенства). Пусть даны два ряда с положительными членами:
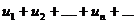 (2.5)
(2.5)
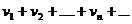 (2.6)
(2.6)
причем члены первого ряда не превосходят членов второго при любом 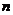 , т.е.
, т.е.
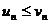 (2.7)
(2.7)
Тогда: а) если сходится ряд (2.6), то сходится и ряд (2.5)
б) если расходится ряд (2.5), то расходится и ряд (2.6).
Удобно применять другую формулировку этой теоремы:
а) если больший ряд сходится, то меньший ряд тоже сходится;
б) если меньший ряд расходится, то больший ряд тоже расходится.
Примеры
Исследовать сходимость следующих рядов:
1) 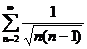
Решение. Сравним данный ряд с гармоническим 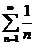 , мысленно отбросив его первый член, равный 1 (что, естественно, не повлияет на сходимость ряда). Т.к.
, мысленно отбросив его первый член, равный 1 (что, естественно, не повлияет на сходимость ряда). Т.к. 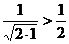 ,
, 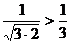 , и вообще,
, и вообще, 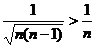 (ведь
(ведь 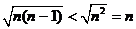 ), то члены данного ряда больше членов расходящегося гармонического ряда, и, следовательно, на основании признака сравнения данный ряд расходится.
), то члены данного ряда больше членов расходящегося гармонического ряда, и, следовательно, на основании признака сравнения данный ряд расходится.
Понятно, что для применения признака сравнения в форме неравенства нужно сначала установить подходящее неравенство. При этом часто пользуются следующими стандартными неравенствами:
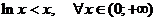 , (2.8)
, (2.8)
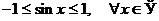 ,
,
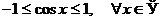 .
.
Иногда приходится применять более сложные неравенства:
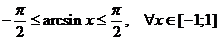 ,
,
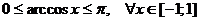 ,
,
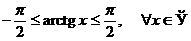 ,
,
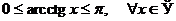 ,
,
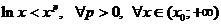 при некотором
при некотором 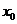 .
.
2) 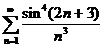
Решение. Прежде всего, заметим, что это ряд с положительными членами, т.к. синус возводится в четную степень. Далее очевидное неравенство 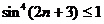 позволяет заключить, что
позволяет заключить, что 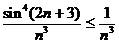 , а поскольку ряд
, а поскольку ряд 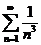 сходится, то и ряд с меньшими членами
сходится, то и ряд с меньшими членами 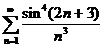 тоже сходится.
тоже сходится.
3) 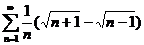
Решение. Преобразуем выражение, стоящее под знаком суммы, следующим образом:
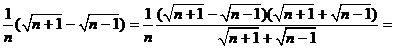
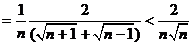
(здесь мы учли, что 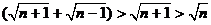 ).
).
Т.к. ряд 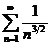 – сходится (как обобщенный гармонический при
– сходится (как обобщенный гармонический при 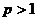 ), то исследуемый ряд также сходится.
), то исследуемый ряд также сходится.
Отметим «эталонные» ряды, часто используемые для сравнения:
а) геометрический ряд 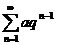 – сходится при
– сходится при 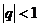 , расходится при
, расходится при 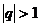 ,
,
б) обобщенный гармонический ряд 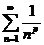 сходится при
сходится при 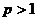 и расходится при
и расходится при 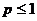 .
.
Нестандартность применения признака сравнения заключается в том, что надо не только подобрать соответствующий «эталонный» ряд, но и доказать неравенство (2.7), для чего часто требуется преобразование рядов (например, отбрасывание или приписывание конечного числа членов, умножение на определенные числа и т. п.). Более простым оказывается признак сравнения в предельной форме – ведь вычислять пределы обычно гораздо проще, чем доказывать неравенства.
Теорема.Второй признак сравнения (признак сравнения в предельной форме). Если 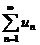 и
и 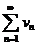 – ряды с положительными членами и существует предел отношения их общих членов
– ряды с положительными членами и существует предел отношения их общих членов 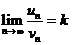 , причем
, причем 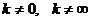 , то ряды ведут себя одинаково: либо одновременно сходятся, либо одновременно расходятся.
, то ряды ведут себя одинаково: либо одновременно сходятся, либо одновременно расходятся.
Чаще всего исследуемый ряд сравнивают с обобщенным гармоническим рядом 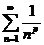 , причем p удобно подбирать в процессе сравнения, как это сделано ниже в примере 1.
, причем p удобно подбирать в процессе сравнения, как это сделано ниже в примере 1.
Примеры
1) 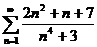
Решение. Сравним данный ряд с обобщенным гармоническим рядом 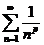 , причем p подберем в процессе сравнения.
, причем p подберем в процессе сравнения.
Выпишем предел 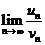 и преобразуем его:
и преобразуем его:
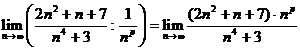 (2.9)
(2.9)
Мы пришли к пределу отношения двух степенных выражений на бесконечности. Если степень числителя меньше степени знаменателя, то предел равен 0, а это тот случай, когда признак сравнения в предельной форме не работает. Если степень числителя больше степени знаменателя, то предел равен 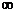 , а это опять тот случай, когда признак сравнения в предельной форме не работает. Таким образом, нас устроит только случай, когда степень числителя равна степени знаменателя, т.е.
, а это опять тот случай, когда признак сравнения в предельной форме не работает. Таким образом, нас устроит только случай, когда степень числителя равна степени знаменателя, т.е. 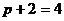 , или
, или 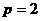 (в этом случае предел равен отношению старших коэффициентов, т.е. не 0 и не
(в этом случае предел равен отношению старших коэффициентов, т.е. не 0 и не 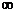 ). Итак, исследуемый ряд ведет себя так же, как и ряд
). Итак, исследуемый ряд ведет себя так же, как и ряд 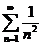 , т.е. сходится.
, т.е. сходится.
Разумеется, решение похожих задач не надо расписывать так подробно. Обычно, выписав предел (2.9), далее пишут 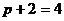
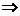
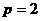
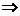 сходится. Ясно, что слово «сходится» относится сразу к двум рядам и к
сходится. Ясно, что слово «сходится» относится сразу к двум рядам и к 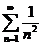 , и к исходному ряду.
, и к исходному ряду.
Следствием второго (предельного) признака сравнения является третий признак сравнения.
Теорема.Третий признак сравнения (признак сравнения в форме эквивалентных б.м. или кратко эквивалентный признак сравнения). В общем члене ряда бесконечно малый множитель или делитель можно заменить на эквивалентный, поведение ряда (сходимость или расходимость) от этого не изменится.
Замечание 1. Напомним таблицу эквивалентных бесконечно малых величин (при 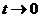 ):
):
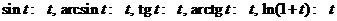 .
.
Замечание 2. При работе с эквивалентным признаком сравнения необходимо помнить, что таблица эквивалентных бесконечно малых величин выписана при 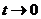 , а в рядах всегда
, а в рядах всегда 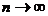 , т.е. n является бесконечно большой. А вот бесконечно малыми являются величины вида:
, т.е. n является бесконечно большой. А вот бесконечно малыми являются величины вида: 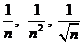 (и вообще
(и вообще 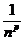 при
при 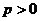 ),
), 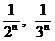 (и вообще
(и вообще 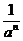 при
при 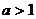 ).
).
2) 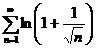
Решение. Т.к. при 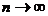
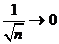 (т.е.
(т.е. 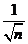 – б.м.), то
– б.м.), то 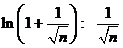 , и ряд
, и ряд 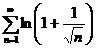 ведет себя так же, как и ряд
ведет себя так же, как и ряд 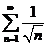 – обобщенный гармонический ряд при p=1/2<1, т.е. расходится.
– обобщенный гармонический ряд при p=1/2<1, т.е. расходится.
На практике запись ведут кратко:
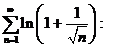
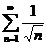 – расходится. Ясно, что слово «расходится» относится к обоим рядам.
– расходится. Ясно, что слово «расходится» относится к обоим рядам.
3) 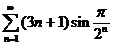 .
.
Решение. Т.к. 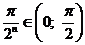 ,то
,то 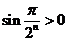 , ряд
, ряд 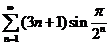 знакоположительный, и к нему можно применять эквивалентный признак сравнения. Поскольку
знакоположительный, и к нему можно применять эквивалентный признак сравнения. Поскольку 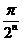 – б.м. при
– б.м. при 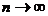 , то
, то 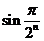
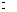
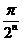 и
и 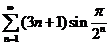
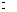
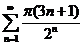 =
= 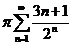 .
.
Последний ряд легко исследуется по признаку Даламбера (он сходится).
Несмотря на то, что предельный и эквивалентный признаки сравнения более просты по сравнению с признаком сравнения в форме неравенства, иногда без первого признака не обойтись. Покажем это на следующем примере, а заодно продемонстрируем, как надо рассуждать в общем и целом при исследовании рядов на сходимость.
4) 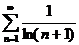
Решение. Проверим необходимый признак: 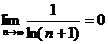 – необходимый признак не работает. Попробуем применить признак Даламбера:
– необходимый признак не работает. Попробуем применить признак Даламбера:
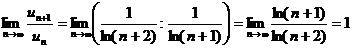 ,
,
т.е. вопрос о сходимости ряда остается открытым. Этого следовало ожидать (см. замечание к признаку Даламбера).
Применим признак сравнения в предельной форме. Сравним данный ряд, например, с гармоническим рядом:
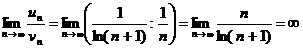 ,
,
т.е. ответа о сходимости ряда нет. Аналогичная картина наблюдается и при использовании других «эталонных» рядов.
Применим, наконец, признак сравнения в форме неравенства (первый признак сравнения). Сравним данный ряд с гармоническим, у которого отброшен первый член: 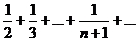 ... Т.к. члены рассматриваемого ряда больше членов расходящегося гармонического
... Т.к. члены рассматриваемого ряда больше членов расходящегося гармонического 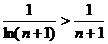 , что вытекает из неравенства (2.8), то данный ряд расходится.
, что вытекает из неравенства (2.8), то данный ряд расходится.
Отметим, что для исследования сходимости данного ряда неприменим и интегральный признак, т.к. первообразная подынтегральной функции не является элементарной функцией, т.е. соответствующий неопределенный интеграл 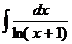 является «не берущимся».
является «не берущимся».
Задачи
А) Исследовать ряды с помощью признака Даламбера:
1. 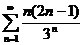 2.
2. 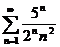 3.
3. 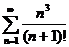
4. 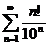 5.
5. 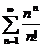 6.
6. 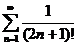
B) Исследовать ряды с помощью радикального признака Коши:
7. 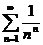 8.
8.  9.
9. 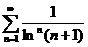 10.
10. 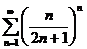
C) Исследовать ряды с помощью интегрального признака Коши:
11. 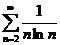 12.
12. 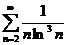 13.
13. 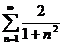
14. 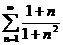 15.
15. 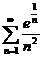
D) Исследовать ряды с помощью признаков сравнения:
16. 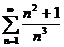 17.
17. 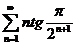 18.
18. 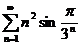
19. 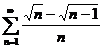 20.
20. 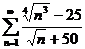 21.
21. 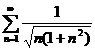
Е) Исследовать ряды на сходимость:
22. 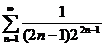 23.
23. 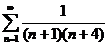 24.
24. 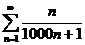
25. 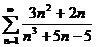 26.
26. 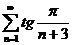 27.
27. 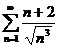
28. 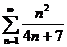 29.
29. 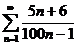 30.
30. 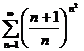
31. 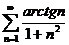 32.
32. 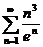 33.
33. 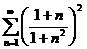
34. 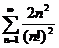 35.
35. 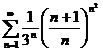 36.
36. 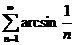
37 . 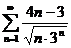 38.
38. 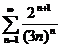 39.
39. 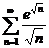
40. 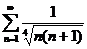 41.
41. 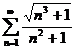 42.
42. 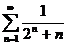
43. 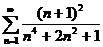 44.
44. 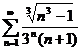 .
.
Примеры
Исследовать на сходимость следующие ряды:
1) 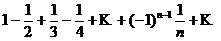
Решение. Т.к. члены данного ряда по абсолютной величине монотонно убывают: 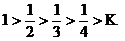 , и вообще,
, и вообще, 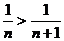 , а общий член ряда при
, а общий член ряда при 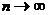 стремится к нулю, то в силу признака Лейбница ряд сходится.
стремится к нулю, то в силу признака Лейбница ряд сходится.
2) 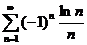 .
.
Решение. Проверим условие (3.2): 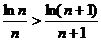 . Доказать это неравенство достаточно сложно. Поэтому применим следующий прием: докажем, что функция
. Доказать это неравенство достаточно сложно. Поэтому применим следующий прием: докажем, что функция 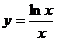 монотонно убывает на некотором интервале вида
монотонно убывает на некотором интервале вида 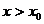 с помощью вычисления производной и исследования функции (это уже было сделано в §2, раздел IV, пример 2). В нашем случае
с помощью вычисления производной и исследования функции (это уже было сделано в §2, раздел IV, пример 2). В нашем случае 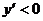 при
при 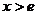 , и функция монотонно убывает в данном промежутке. Следовательно, неравенства (3.2) выполняются для любых
, и функция монотонно убывает в данном промежутке. Следовательно, неравенства (3.2) выполняются для любых 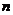 , начиная с трех.
, начиная с трех.
Проверим условие (3.3). Для этого необходимо вычислить 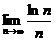 . Используя правило Лопиталя, получим
. Используя правило Лопиталя, получим 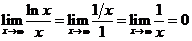 . Следовательно, и
. Следовательно, и 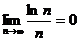 .
.
Т.о., оба условия теоремы Лейбница выполняются, и, следовательно, данный ряд сходится.
Определение. Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные.
Очевидно, знакочередующиеся ряды являются частным случаем знакопеременных.
Предполагаем теперь, что в записи
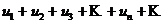 (3.4)
(3.4)
имеются как положительные, так и отрицательные 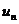 .
.
Теорема. (Модульный признак сходимости знакопеременных рядов).
Если ряд, составленный из абсолютных величин членов данного знакопеременного ряда (3.4):
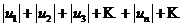 (3.5)
(3.5)
сходится, то сходится и данный ряд.
Отметим, что если ряд (3.5) расходится, то отсюда не следует, что ряд (3.4) будет также расходящимся. Например, ряд 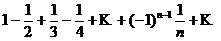 сходится по признаку Лейбница, а ряд из абсолютных величин его членов (гармонический ряд)
сходится по признаку Лейбница, а ряд из абсолютных величин его членов (гармонический ряд) 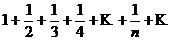 расходится.
расходится.
В связи с этим можно ввести понятие абсолютной и условной сходимости:
Определение. Знакопеременный ряд 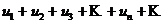 называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов
называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов 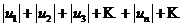 .
.
Определение. Знакопеременный ряд 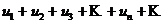 называется условно сходящимся, если ряд, составленный из абсолютных величин
называется условно сходящимся, если ряд, составленный из абсолютных величин 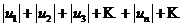 , расходится, а сам ряд сходится.
, расходится, а сам ряд сходится.
Например, ряд 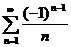 является условно сходящимся (см. пример 1). А ряд
является условно сходящимся (см. пример 1). А ряд 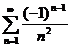 является абсолютно сходящимся, т.к. ряд, составленный из абсолютных величин
является абсолютно сходящимся, т.к. ряд, составленный из абсолютных величин 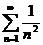 , сходится (обобщенный гармонический при
, сходится (обобщенный гармонический при 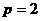 ).
).
Грубо говоря, различие между абсолютно и условно сходящимися рядами заключается в следующем: абсолютно сходящиеся ряды сходятся в основном в силу того, что их члены быстро убывают, а условно сходящиеся – в результате того, что положительные и отрицательные слагаемые частично уничтожают друг друга.
Свойства абсолютно и условно сходящихся рядов существенно различаются: абсолютно сходящиеся ряды по своим свойствам напоминают конечные суммы: их можно складывать, перемножать, переставлять местами члены ряда. Условно сходящиеся ряды такими свойствами не обладают. Возьмем, например, условно сходящийся ряд 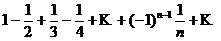 . Переставим члены ряда местами и сгруппируем их следующим образом:
. Переставим члены ряда местами и сгруппируем их следующим образом:
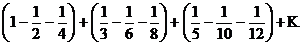
Перепишем ряд в виде (произведя первое действие в каждой скобке):
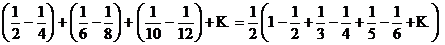
Видим, что от перестановки членов ряда сумма его уменьшилась в 2 раза.
Можно показать (теорема Римана), что от перестановки членов условно сходящегося ряда можно получить ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд.
Примеры
Исследовать ряды на абсолютную и условную сходимость.
1) 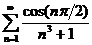
Решение. Ряд, составленный из абсолютных величин членов данного ряда: 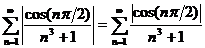 сходится по признаку сравнения, т.к.
сходится по признаку сравнения, т.к. 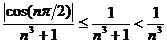 , а ряд
, а ряд 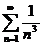 – сходится (обобщенный гармонический ряд при
– сходится (обобщенный гармонический ряд при 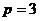 ). Следовательно, данный ряд является абсолютно сходящимся.
). Следовательно, данный ряд является абсолютно сходящимся.
2) 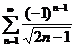
Решение. Составим ряд из абсолютных величин членов данного ряда: 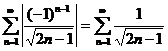 . Исследуем этот ряд на сходимость с помощью предельного признака сравнения, сравнив его с эталонным рядом
. Исследуем этот ряд на сходимость с помощью предельного признака сравнения, сравнив его с эталонным рядом 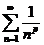 (p подберем в процессе сравнения), имеем
(p подберем в процессе сравнения), имеем 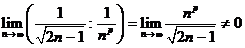 и
и 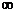 лишь при равенстве степеней числителя и знаменателя, т.е. при
лишь при равенстве степеней числителя и знаменателя, т.е. при 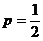 , следовательно, сравниваемые ряды являются расходящимися. Таким образом, ряд, составленный из модулей, расходится, и абсолютной сходимости нет.
, следовательно, сравниваемые ряды являются расходящимися. Таким образом, ряд, составленный из модулей, расходится, и абсолютной сходимости нет.
Исследуем данный знакочередующийся ряд с помощью признака Лейбница. Очевидно, что:
1) 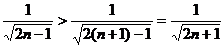 , 2)
, 2) 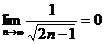 .
.
Оба пункта признака Лейбница выполнены, следовательно, данный ряд условно сходится.
Задачи
Исследовать ряды на абсолютную и условную сходимость:
45. 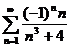 46.
46. 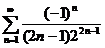 47.
47. 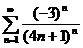
48. 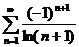 49.
49. 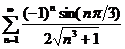 50.
50. 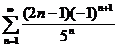
51. 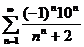 52.
52. 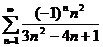 53.
53. 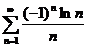
54. 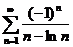 55.
55. 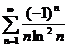 56.
56. 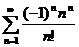
57. 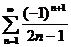 58.
58. 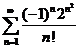 59.
59. 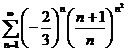
Степенные ряды
До сих пор мы рассматривали ряды, членами которых были числа, т.е. числовые ряды. Перейдем к рассмотрению рядов, членами которых являются функции, в частности, степенные функции с целыми неотрицательными показателями степени:
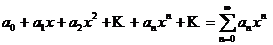 (4.1)
(4.1)
Определение. Ряд вида (4.1) называется степенным, а числа 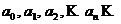 называются коэффициентами степенного ряда.
называются коэффициентами степенного ряда.
Рассматривают и степенные ряды более общего вида:
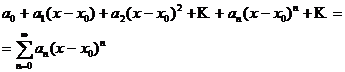 (4.2)
(4.2)
(по степеням 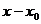 ). Такой ряд не отличается существенно от ряда вида (4.1), ибо приводится к нему простой заменой переменной:
). Такой ряд не отличается существенно от ряда вида (4.1), ибо приводится к нему простой заменой переменной: 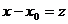 .
.
Определение. Множество значений 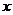 , при которых степенной ряд (4.1) или (4.2) сходится, называется областью сходимости степенного ряда.
, при которых степенной ряд (4.1) или (4.2) сходится, называется областью сходимости степенного ряда.
Структура области сходимости степенного ряда устанавливается с помощью следующей теоремы:
Теорема Абеля
1) Если степенной ряд вида (4.1), т.е. по степеням 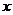 , сходится при значении
, сходится при значении 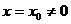 (отличном от нуля), то он сходится, и притом абсолютно, при всех значениях
(отличном от нуля), то он сходится, и притом абсолютно, при всех значениях 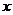 таких, что
таких, что 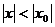 .
.
2) Если степенной ряд вида (4.1) расходится при значении 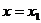 , то он расходится при всех значениях
, то он расходится при всех значениях 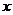 таких, что
таких, что 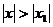 .
.
Из теоремы Абеля вытекает следующая теорема.
Теорема. Областью сходимости степенного ряда вида (4.2), т.е. ряда по степеням 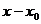 , является интервал с центром в точке
, является интервал с центром в точке 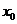 и с концами в точках
и с концами в точках 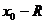 и
и 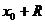 .
.
Число 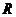 получило название радиуса сходимости, а интервал
получило название радиуса сходимости, а интервал 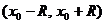 – интервала сходимости степенного ряда. На концах интервала сходимости, т.е. при
– интервала сходимости степенного ряда. На концах интервала сходимости, т.е. при 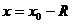 и
и 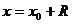 вопрос о сходимости или расходимости данного ряда решается индивидуально для каждого конкретного ряда.
вопрос о сходимости или расходимости данного ряда решается индивидуально для каждого конкретного ряда.
У некоторых рядов интервал сходимости вырождается в точку 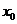 (при
(при 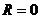 ), у других охватывает всю числовую ось (при
), у других охватывает всю числовую ось (при 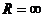 ).
).
Для начала укажем способ определения интервала сходимости степенного ряда на примере ряда (4.1).
Рассмотрим ряд, составленный из абсолютных величин членов этого ряда:
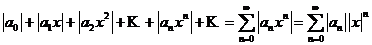 (4.3)
(4.3)
Т.к. при каждом конкретном 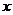 ряд (4.3) является числовым знакоположительным рядом, то для выяснения вопроса о его сходимости можно воспользоваться признаком Даламбера:
ряд (4.3) является числовым знакоположительным рядом, то для выяснения вопроса о его сходимости можно воспользоваться признаком Даламбера:
Допустим, что существует
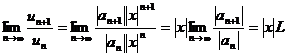 .
.
Тогда, по признаку Даламбера ряд сходится, если 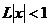 (т.е. при
(т.е. при 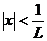 ), и расходится, если
), и расходится, если 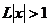 (т.е. при
(т.е. при 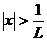 ).
).
Следовательно, ряд (4.1) сходится абсолютно
