Расчет цепей при смешанном соединении элементов

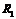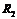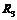На рис.9 приведена цепь при смешанном соединении линейного сопротивления и двух нелинейных и ВАХ которых приведены на рис.10. Требуется определить установившиеся значения токов 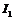, , 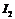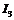и напряжений на элементах при заданной ЭДС .

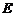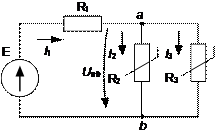
Рис.9. Цепь со смешанным соединением элементов

Сначала находим ВАХ параллельного участка 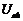путем сложения абсцисс 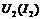и 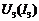при одинаковых напряжениях. Далее складывая ординаты характеристик 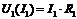и 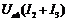, находим результирующую ВАХ всей цепи 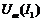. Порядок построения показан на рис.10 стрелками.

Рис.10. Расчет цепи при смешанном соединении

Пересечения последней кривой с линией Е – точка А, позволяет определить ток 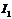и напряжения 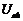на параллельном участке. Пересечение линии напряжения 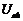с кривым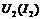и и 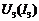определяет токи ветвей , .

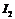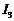1.2.4. Преобразование активных нелинейных двухполюсников

Рассмотрим цепь с последовательно соединенными нелинейным сопротивлением 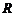с Э.Д.С. постоянного тока 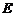(рис.11).

Рис. 11. Преобразование двухполюсников

а) активный двухполюсник с ЭДС; б,в) построение ВАХ двухполюсника

На основании второго закона Кирхгофа имеем:

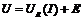, (6)

Из последнего уравнения следует, что ВАХ рассматриваемой цепи может быть получена суммированием ординат 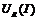и ЭДС 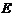, т.е. путем смещения ВАХ на 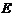вверх по ординате, если 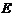>0 и вниз если 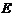<0 (рис.11.б, в).

Рис. 12. Преобразование двухполюсников

а) активный двухполюсник с источником тока;

б,в) построение ВАХ двухполюсника

ВАХ активного двухполюсника, представляющее собой параллельное соединение нелинейного сопротивления 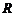и источника постоянного тока 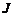, получается путем смещения ВАХ нелинейного элемента 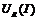вдоль оси тока на 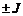(рис.12.б,в).

Преобразованием двухполюсников пользуются не только для решения прямой задачи, но и для решения обратной задачи: заменить нелинейный двухполюсник, ВАХ которого не проходит через начало координат, нелинейным сопротивлением и идеализированным источником постоянного тока.

Рис.13. К решению обратной задачи

а) активный двухполюсник; б) ВАХ двухполюсника; в) ВАХ нелинейного сопротивления; г) схема замещения двухполюсника.

Покажем это на конкретном примере. Пусть активный двухполюсник (рис.13.а) имеет ВАХ, показанную на рис.13.б. Представим двухполюсник схемой замещения на рис.13.г. Из выражения (6) следует:

.

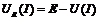Для нелинейного сопротивления 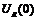=0, получим 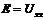, тогда можно записать:

.

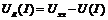ВАХ нелинейного сопротивления получается путем вычитания 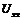из ординат ВАХ двухполюсника 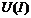. В итоге получаем ВАХ нелинейного сопротивления 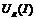на рис.13.в.

Анализ разветвленных цепей

Расчет разветвленных цепей графическим способом рассмотрим на конкретном примере цепи на рис.14.а. ВАХ нелинейных элементов для упрощения графических построений приняты одинаковыми и приведены на рис. 6.14.б.

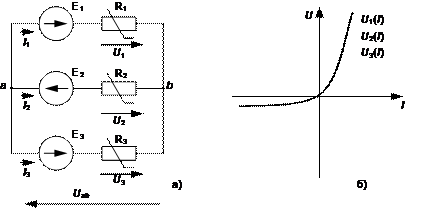
Рис.14. Расчет разветвленной цепи

а) схема цепи; б) ВАХ нелинейных элементов

Выбираем положительное направление токов в ветвях. Согласно второму закону Кирхгофа для напряжения 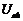можем записать:

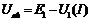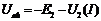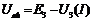; ; . (7)

Считая каждую ветвь активным двухполюсником, строим их ВАХ. (см. рис.15.). ВАХ двухполюсника получается сдвигом ВАХ резистивного элемента на соответствующую ЭДС. Предварительно ВАХ резистивного элемента необходимо отразить относительно оси абсцисс, т.к. в уравнения (7) они входят со знаком минус.

Согласно первому закону Кирхгофа имеем:

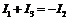. (8)

Поэтому для нахождения точки установившегося режима строим вспомогательную кривую 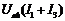, для чего при одинаковых напряжениях складываем абсциссы кривых 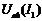и .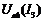

Рис.15. Построение для разветвленной цепи

Точка пересечения кривых 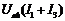и 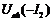- точка А и определяет решение: напряжение 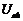, токи ветвей , , .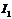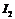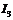