Вогнутость и выпуклость функции. Точки перегиба
Определение. График функции  , определенной и непрерывной на отрезке
, определенной и непрерывной на отрезке 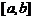 ,называется выпуклым (вогнутым), если каждая дуга графика функции
,называется выпуклым (вогнутым), если каждая дуга графика функции  лежит не ниже
лежит не ниже
(не выше) стягивающей ее хорды (рис. 10.4), т. е. 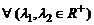 :
: 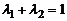 ,
, 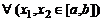 Þ
Þ
Þ 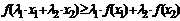 ; (
; ( 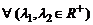 :
: 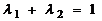 ,
, 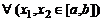 Þ
Þ 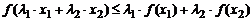 ).
).
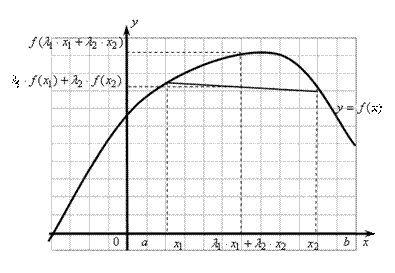
Рис. 10.4
Теорема 10.5 (Достаточное условие вогнутости / выпуклости). Если для дважды дифференцируемой функции  вторая производная
вторая производная 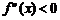 (
( 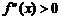 ) на интервале
) на интервале 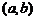 , то график функции на этом интервале выпуклый (вогнутый).
, то график функции на этом интервале выпуклый (вогнутый).
Определение. Точкой перегиба графика дифференцируемой функ-ции  называется такая его точка, при переходе через которую кривая меняет выпуклость на вогнутость или наоборот (рис. 10.5).
называется такая его точка, при переходе через которую кривая меняет выпуклость на вогнутость или наоборот (рис. 10.5).
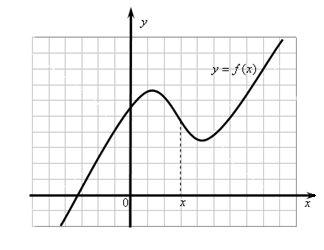
Рис. 10.5
Теорема 10.6 (Необходимое условие точки перегиба). Если 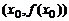 – точка перегиба функции
– точка перегиба функции  , то вторая производ-ная этой функции
, то вторая производ-ная этой функции 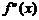 в точке
в точке 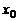 равна нулю или не существует.
равна нулю или не существует.
Теорема 10.7 (Достаточное условие точки перегиба). Если для функции  вторая производная
вторая производная 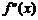 в некоторой точке
в некоторой точке 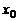 обращается в ноль или не существует и при переходе через эту точку меняет свой знак, то точка
обращается в ноль или не существует и при переходе через эту точку меняет свой знак, то точка 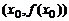 является точкой перегиба графика функции.
является точкой перегиба графика функции.
Асимптоты графика функции
Определение. Асимптотой графика функции называется прямая, к которой неограниченно приближается текущая точка кривой при удалении этой функции в бесконечность.
Определение. Прямая 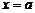 называется вертикальной асимп-тотой графика функции
называется вертикальной асимп-тотой графика функции  , если хотя бы один из односто-ронних пределов
, если хотя бы один из односто-ронних пределов 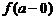 или
или 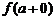 равен бесконечности.
равен бесконечности.
Определение. Прямая, заданная уравнением 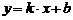 , назы-вается наклонной асимптотой графика функции
, назы-вается наклонной асимптотой графика функции  при
при 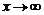 , если коэффициенты k, b, определяемые по формулам
, если коэффициенты k, b, определяемые по формулам 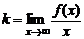 ,
, 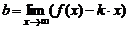 , принимают конечные значения.
, принимают конечные значения.
Если 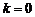 , то
, то 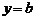 – горизонтальная асимптота.
– горизонтальная асимптота.
Схема исследования функции
Для того чтобы построить график функции, необходимо обладать достаточной информацией об этой функции. Такую информацию можно получить, проведя полное исследование функции, пользуясь следующей схемой:
1)область определения функции;
2)нули функции, интервалы знакопостоянства функции;
3)четность, нечетность, периодичность;
4)экстремумы, интервалы возрастания / убывания функции;
5)точки перегиба, интервалы выпуклости / вогнутости;
6)асимптоты.
Пример 10.2. Провести полное исследование функции 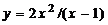 и построить ее график.
и построить ее график.
Решение. Исследуем функцию в соответствии со схемой.
1)Функция 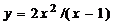 не определена только в точке
не определена только в точке 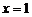 , поэтому областью определения функции будет вся числовая плоскость, кроме этой точки, то есть
, поэтому областью определения функции будет вся числовая плоскость, кроме этой точки, то есть 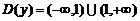 .
.
2)Найдем точки пересечения графика функции с осями координат:
с осью Ох: 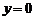 Þ
Þ 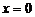 ; с осью Оу:
; с осью Оу: 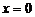 Þ
Þ 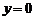 . Определим интервалы знакопостоянства функции (рис. 10.6).
. Определим интервалы знакопостоянства функции (рис. 10.6).

Рис. 10.6
Таким образом, график функции расположен выше оси Ox на интервале 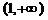 и ниже – на интервале
и ниже – на интервале 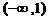 .
.
3)Очевидно, что ни одна позиция не выполнена, то есть функция не является ни четной, ни нечетной, ни периодической.
4)Исследуем функцию на наличие экстремумов. Для этого вычислим первую производную:
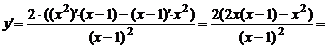
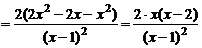 .
.
Найдем точки, в которых производная равна нулю или не существует, отметим на числовой оси полученные точки и определим знак производной на каждом из полученных интервалов (рис. 10.7).

Рис. 10.7
Функция возрастает на интервалах 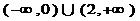 , убывает
, убывает 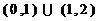 , в точке
, в точке 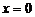 ,
, 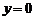 достигает мак-симум, в точке
достигает мак-симум, в точке 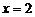 ,
, 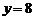 достигает минимум.
достигает минимум.
5) 
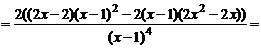
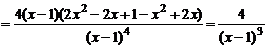 .
.
Найдем точки, в которых вторая производная функции равна нулю или не существует, полученную точку отметим на числовой оси и проверим знак второй производной на полученных интервалах (рис. 10.8).
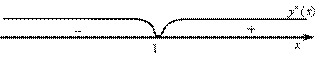
Рис. 10.8
График функции – выпуклый на интервале 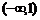 , вогнутый – на интервале
, вогнутый – на интервале 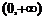 ; так как функция в точке
; так как функция в точке 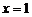 не определена, то точек перегиба нет.
не определена, то точек перегиба нет.
6)Поскольку функция не определена в точке 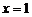 , вычислим пределы функции справа и слева в этой точке.
, вычислим пределы функции справа и слева в этой точке.
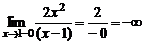 ,
, 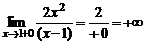 .
.
Прямая 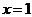 является вертикальной асимптотой.
является вертикальной асимптотой.
Исследуем функцию на наличие наклонной асимптоты, для этого вычислим коэффициенты k и b.
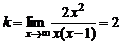 ;
; 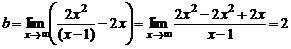 .
.
Прямая 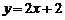 является наклонной асимптотой.
является наклонной асимптотой.
Результаты исследования представим в следующей таблице:
| x | 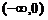 | (0, 1) | (1, 2) | 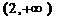 | ||
| y | – | – ¯ | + ¯ | + | ||
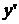 | + | Max | – | – | Min | + |
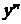 | – | – | + | + |
Построим график функции (рис. 10.9).
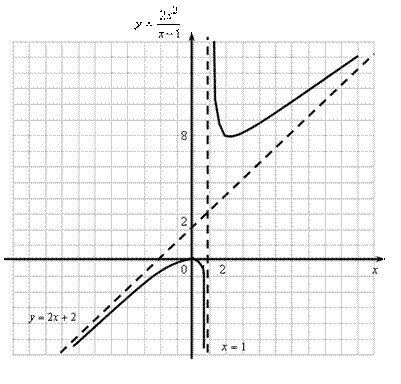 Рис. 10.9
Рис. 10.9
ЗАКЛЮЧЕНИЕ
В 1-м семестре выполняются две контрольные работы (1-я контрольная работа включает задания с 1-го по 6-е, 2-я контрольная работа – задания с 7-го по 12-е), вариант которых следует выбирать по последней цифре номера зачетной книжки. Если номер заканчивается 0, то он соответствует варианту 10. Не следует приступать к выполнению контрольных работ, не изучив соответствующие разделы и не разобрав приведенные в них примеры.
Контрольные работы оформляются в отдельной тетради (необходимо оставить поля для замечаний рецензента) либо в отдельном файле (в названии файла следует указать фамилию и дисциплину), если Ваш населенный пункт расположен в ином городе, чем сам вуз, в котором Вы обучаетесь. Условие задачи должно быть приведено полностью. Решение выполняется в логи-ческой последовательности с пояснениями и краткими форму-лировками производимых действий.
Выполненные контрольные работы студентом доставляются в институт или отправляются по электронной почте на рецензирование (vm2@kemtipp.ru). Получив проверенную работу, студент должен учесть замечания и исправить ошибки, если таковые имеются. Если работа не зачтена, то ее надо выслать на повторное рецензирование. Контрольные работы, выполненные без соблюдения предъявляемых требований, небрежно или не своего варианта, не рецензируются.
Возникающие при выполнении контрольной работы вопросы можно задать по электронной почте (vm2@kemtipp.ru).
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Задание № 1.Даны четыре вектора 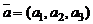 ,
, 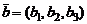 ,
, 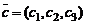 и
и 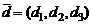 в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы 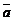 ,
, 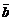 ,
, 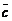 образуют базис, и найти координаты вектора
образуют базис, и найти координаты вектора 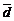 в этом базисе.
в этом базисе.
1) 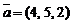 ,
, 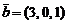 ,
, 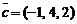 ,
, 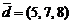 ;
;
2) 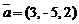 ,
, 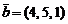 ,
, 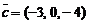 ,
, 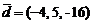 ;
;
3) 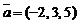 ,
, 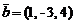 ,
, 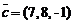 ,
, 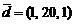 ;
;
4) 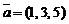 ,
, 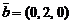 ,
, 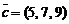 ,
, 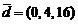 ;
;
5) 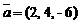 ,
, 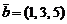 ,
, 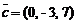 ,
, 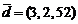 ;
;
6) 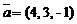 ,
, 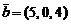 ,
, 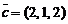 ,
, 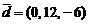 ;
;
7) 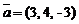 ,
, 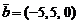 ,
, 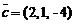 ,
, 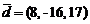 ;
;
8) 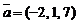 ,
, 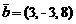 ,
, 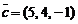 ,
, 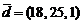 ;
;
9) 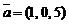 ,
, 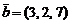 ,
, 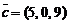 ,
, 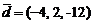 ;
;
10) 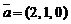 ,
, 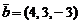 ,
, 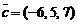 ,
, 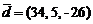 .
.
Задание № 2.Дана система трех линейных алгебра-ических уравнений с тремя неизвестными. Требуется: 1) найти ее решение с помощью правила Крамера; 2) записать систему в матричной форме и решить ее средствами матричного исчисле-ния, при этом правильность вычисления обратной матрицы прове-рить, используя матричное умножение; 3) решить методом Гаусса.
| 1. | 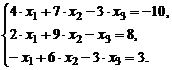 | 6. |  |
| 2. | 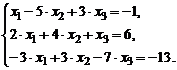 | 7. | 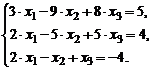 |
| 3. | 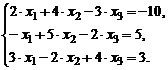 | 8. | 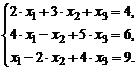 |
| 4. | 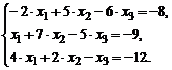 | 9. | 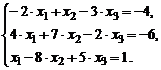 |
| 5. | 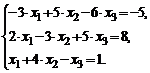 | 10. | 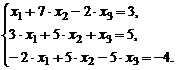 |
Задание № 3.Даны координаты вершин пирамиды. Найти:
1) длины ребер АВ и AC; 2) угол между ребрами АВ и АС;
3) площадь грани АВС; 4) объем пирамиды ABCD; 5) уравнение прямой АВ; 6) уравнение плоскости АВС; 7) уравнение высоты пирамиды, опущенной на грань АВС. Сделать чертеж.
1) 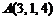 ,
, 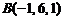 ,
, 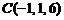 ,
, 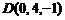 ;
;
2) 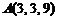 ,
, 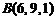 ,
, 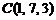 ,
, 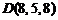 ;
;
3) 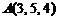 ,
, 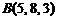 ,
, 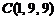 ,
, 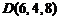 ;
;
4) 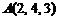 ,
, 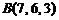 ,
, 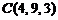 ,
, 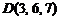 ;
;
5) 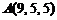 ,
, 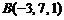 ,
, 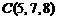 ,
, 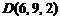 ;
;
6) 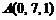 ,
, 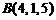 ,
, 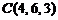 ,
, 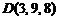 ;
;
7) 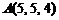 ,
, 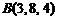 ,
, 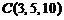 ,
, 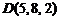 ;
;
8) 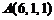 ,
, 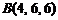 ,
, 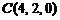 ,
, 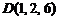 ;
;
9) 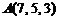 ,
, 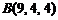 ,
, 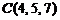 ,
, 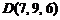 ;
;
10) 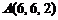 ,
, 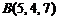 ,
, 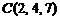 ,
, 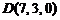 .
.
Задание № 4.Какая кривая определяется следующим уравнением?
1) 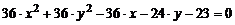 ;
;
2) 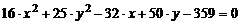 ;
;
3) 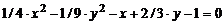 ;
;
4) 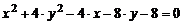 ;
;
5) 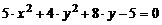 ;
;
6) 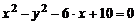 ;
;
7) 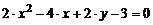 ;
;
8) 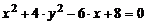 ;
;
9) 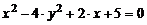 ;
;
10) 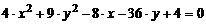 .
.
Задание № 5.Задана линия своим уравнением в полярной системе координат. Необходимо: 1) определить точки, лежащие на линии, придавая j значения через промежуток, равный p/8, начиная от j = 0 и до j = 2p; 2) построить линию, соединив полученные точки; 3) найти уравнение этой линии в прямоугольной декартовой системе координат.
| 1) | 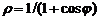 ; ; | 6) | 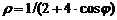 ; ; |
| 2) | 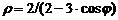 ; ; | 7) | 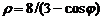 ; ; |
| 3) | 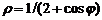 ; ; | 8) | 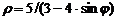 ; ; |
| 4) | 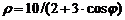 ; ; | 9) | 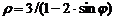 ; ; |
| 5) | 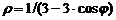 ; ; | 10) | 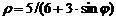 . . |
Задание № 6.Построить множество решений системы линейных алгебраических неравенств и найти координаты угловых точек.
| 1) | 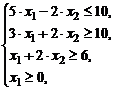 | 6) | 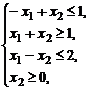 |
| 2) | 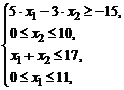 | 7) | 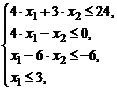 |
| 3) | 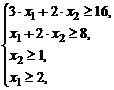 | 8) | 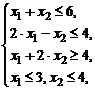 |
| 4) | 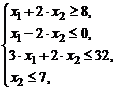 | 9) | 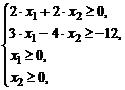 |
| 5) | 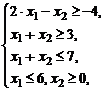 | 10) | 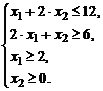 |
Задание № 7.Вычислить пределы функций, не пользу-ясь средствами дифференциального исчисления.
| 1. | а) 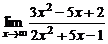 ; ; | б) 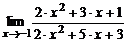 ; ; |
в) 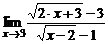 ; ; | г) 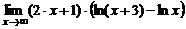 . . | |
| 2. | a) 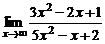 ; ; | б) 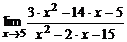 ; ; |
в) 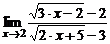 ; ; | г) 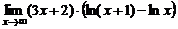 . . | |
| 3. | a) 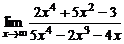 ; ; | б) 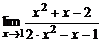 ; ; |
в) 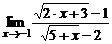 ; ; | г) 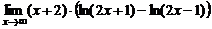 . . | |
| 4. | а) 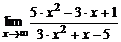 ; ; | б) 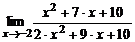 ; ; |
в) 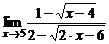 ; ; | г) 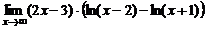 . . | |
| 5. | a) 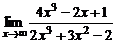 ; ; | б) 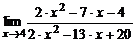 ; ; |
в) 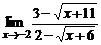 ; ; | г) 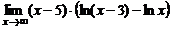 . . | |
| 6. | а) 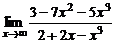 ; ; | б) 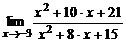 ; ; |
в) 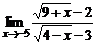 ; ; | г) 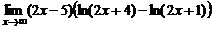 . . | |
| 7. | а) 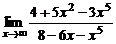 ; ; | б) 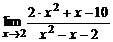 ; ; |
в) 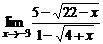 ; ; | г) 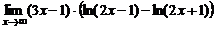 . . | |
| 8. | а) 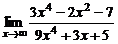 ; ; | б) 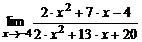 ; ; |
в) 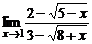 ; ; | г) 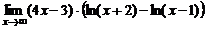 . . | |
| 9. | а) 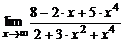 ; ; | б) 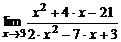 ; ; |
в) 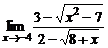 ; ; | г) 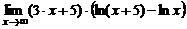 . . | |
| 10. | а) 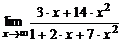 ; ; | б) 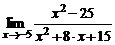 ; ; |
в) 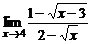 ; ; | г) 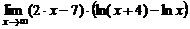 . . |
Задание № 8.Исследовать функцию 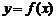 на непрерывность: найти точки разрыва функции (если они есть) и определить их тип. Построить схематический график функции.
на непрерывность: найти точки разрыва функции (если они есть) и определить их тип. Построить схематический график функции.
| 1. | 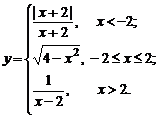 | 6. | 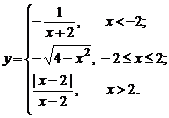 |
| 2. | 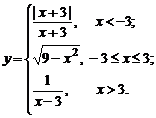 | 7. | 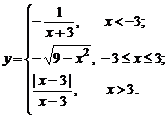 |
| 3. | 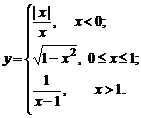 | 8. | 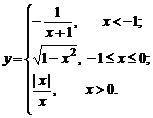 |
| 4. | 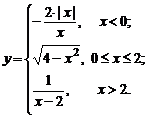 | 9. | 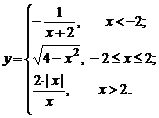 |
| 5. | 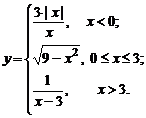 | 10. | 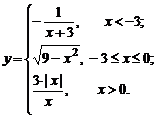 |
Задание № 9.Найти производные первого порядка данной функции, используя правила вычисления производных.
| 1. | 1) 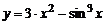 , , | 2) 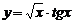 , , |
3) 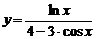 , , | 4) 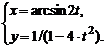 | |
| 2. | 1) 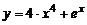 , , | 2) 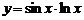 , , |
3) 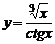 , , | 4) 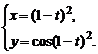 | |
| 3. | 1) 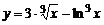 , , | 2) 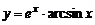 , , |
3) 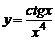 , , | 4) 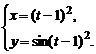 | |
| 4. | 1) 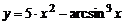 , , | 2) 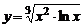 , , |
3) 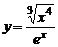 , , | 4) 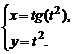 | |
| 5. | 1) 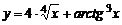 , , | 2) 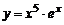 , , |
3) 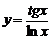 , , | 4) 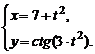 | |
| 6. | 1) 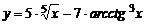 , , | 2) 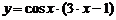 , , |
3) 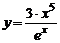 , , | 4) 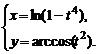 | |
| 7. | 1) 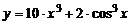 , , | 2) 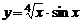 , , |
3) 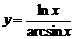 , , | 4) 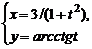 | |
| 8. | 1) 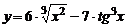 , , | 2) 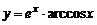 , , |
3) 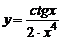 , , | 4) 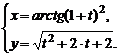 | |
| 9. | 1) 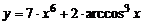 , , | 2) 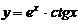 , , |
3) 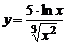 , , | 4) 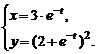 | |
| 10. | 1) 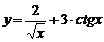 , , | 2) 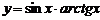 , , |
3) 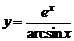 , , | 4) 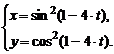 |
Задание № 10.Найти наибольшее и наименьшее значения функции 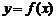 на отрезке
на отрезке 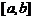 .
.
| 1. | 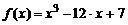 ; ; 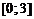 . . |
| 2. | 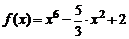 ; ; 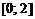 . . |
| 3. | 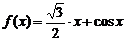 ; ; 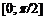 . . |
| 4. | 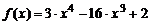 ; ; 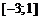 . . |
| 5. | 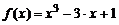 ; ; 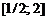 . . |
| 6. | 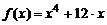 ; ; 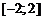 . . |
| 7. | 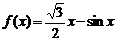 ; ; 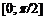 . . |
| 8. | 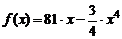 ; ; 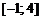 . . |
| 9. | 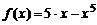 ; ; 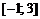 . . |
| 10. | 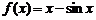 ; ; 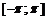 . . |
Задание № 11.Найти уравнение касательной и нормали к гра-фику функции 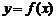 в указанной точке
в указанной точке 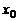 . Сделать чертеж.
. Сделать чертеж.
| 1) | 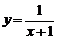 , х0 = 2; , х0 = 2; | 6) | 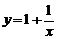 , х0 = 1; , х0 = 1; |
| 2) | 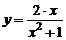 , х0 = 1; , х0 = 1; | 7) | 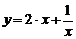 , х0 = 0,5; , х0 = 0,5; |
| 3) | 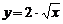 , х0 = 4; , х0 = 4; | 8) | 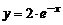 , х0 = 0; , х0 = 0; |
| 4) | 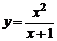 , х0 = –2; , х0 = –2; | 9) | 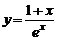 , х0 = 0; , х0 = 0; |
| 5) | 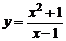 , х0 = 0; , х0 = 0; | 10) | 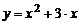 , х0 = –1. , х0 = –1. |
Задание № 12.Построить график функции 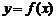 , ис-пользуя общую схему исследования функции.
, ис-пользуя общую схему исследования функции.
| 1) | 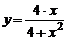 ; ; | 6) | 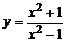 ; ; |
| 2) | 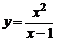 ; ; | 7) | 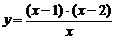 ; ; |
| 3) | 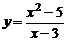 ; ; | 8) | 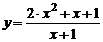 ; ; |
| 4) | 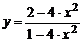 ; ; | 9) | 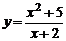 ; ; |
| 5) | 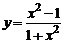 ; ; | 10) | 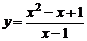 . . |
СПИСОК ЛИТЕРАТУРЫ
1. Данко, П.Е. Высшая математика в упражнениях и за-дачах: в 2 ч. / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Оникс, 2008. – Ч 1. – 304 с.
2. Бугров, Я.С. Высшая математика. Элементы линейной ал-гебры и аналитической геометрии / Я.С. Бугров, С.М. Никольский. – М.: Дрофа, 2003. – 512 с.
3. Пискунов, Н.С. Дифференциальное и интегральное исчис-ление для вузов: в 2 т. / Н.С. Пискунов. – М.: Интеграл-пресс, 2008. – Т. 1. – 416 с.
4. Курош, А.Г. Курс высшей алгебры / А.Г. Курош. – СПб.: Лань, 2008. – 432 с.
5. Демидович, Б.П. Краткий курс высшей математики / Б.П. Демидович, В.А. Кудрявцев. – М.: Астрель; АСТ, 2005. – 654 с.
6. Гантмахер, Ф.Р. Теория матриц / Ф.Р. Гантмахер. – М.: Физматлит, 2004. – 264 с.
7. Проскуряков, И.В. Сборник задач по линейной алгебре / И.В. Проскуряков. – СПб.: Лань, 2008. – 480 с.
8. Натансон, И.П. Краткий курс высшей математики / И.П. На-тансон. – СПб.: Лань, 2007. – 736 с.
9. Мышкис, А.Д. Лекции по высшей математике /А.Д. Мыш-кис. – СПб.: Лань, 2007. – 688 с.
10. Фихтенгольц, Г.М. Курс дифференциального и интеграль-ного исчисления: в 2 т. / Г.М. Фихтенгольц. – СПб.: Лань, 2008. – Т. 1. – 448 с.

УЧЕБНОЕ ИЗДАНИЕ
Иванова Светлана Анатольевна,
ПавскийВалерий Алексеевич
Математика
Учебное пособие
Для студентов вузов
В четырех частях
Часть 1
Нач. редакции А.С. Обвинцева
Редактор А.В. Проскурина
Технический редактор Е.В. Кадочникова
Художественный редактор О.В. Оскорбина
ЛР № 020524 от 02.06.97
Подписано в печать 15.12.10. Формат 60×841/16
Бумага типографская. Гарнитура Times
Уч.-изд. л. 10,25. Тираж 500 экз.
Заказ № 123
ПЛД № 44-09 от 10.10.99
Отпечатано в редакционно-издательском центре
Кемеровского технологического института пищевой промышленности
650010, г. Кемерово, ул. Красноармейская, 52
