ТЕМА 10. Исследование функции
Возрастание и убывание функции
Определение. Функция называется возрастающей (убываю-щей), если при увеличении аргумента значение функции увеличи-вается (уменьшается) (рис. 10.1), то есть соответственно 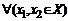 : (
: ( 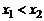 ) Þ (
) Þ ( 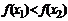 ); (
); ( 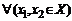 :
: 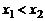 Þ
Þ 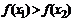 ).
).
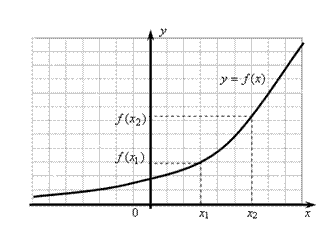
Рис. 10.1
Теорема 10.1. Производная возрастающей (убывающей) функции не отрицательна (не положительна).
Определение. Функция, только возрастающая или убыва-ющая, называется монотонной. Промежутки, на которых данная функция возрастает или убывает, называются промежутками монотонности этой функции.
Экстремумы функции
Определение. Если при переходе аргумента (слева направо) через некоторое значение 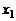 функция переходит от возрастания к убыванию, то говорят, что в точке
функция переходит от возрастания к убыванию, то говорят, что в точке 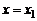 функция имеет максимум (max). Если же при переходе аргумента через некоторое значение
функция имеет максимум (max). Если же при переходе аргумента через некоторое значение 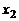 функция переходит от убывания к возрастанию, то в этой точке
функция переходит от убывания к возрастанию, то в этой точке 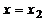 функция имеет минимум (min). Точки максимума и минимума называются точками экстремума (extr) ( рис. 10.2).
функция имеет минимум (min). Точки максимума и минимума называются точками экстремума (extr) ( рис. 10.2).
Теорема 10.2 (необходимое условие экстремума). В точ-ке экстремума дифференцируемой функции производная этой функции равна нулю (см. рис. 10.2).
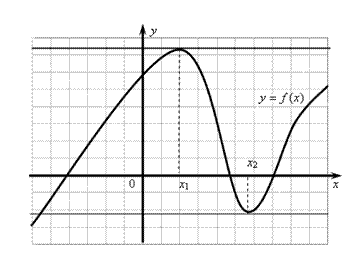
Рис. 10.2
Следствие. Дифференцируемая функция может иметь экс-тремум лишь в тех точках, в которых производная функции рав-на нулю или не существует.
Определение. Точки, в которых производная функции равна нулю или не существует, называются критическими точками функции.
Теорема 10.3 (1-е достаточное условие экстремума). Если дифференцируемая функция  такова, что для некоторого значения
такова, что для некоторого значения 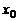 ее аргумента x производная
ее аргумента x производная 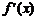 равна нулю (не существует при условии, что сама функция
равна нулю (не существует при условии, что сама функция 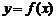 в этой точке непрерывна) и меняет свой знак при переходе через эту точку
в этой точке непрерывна) и меняет свой знак при переходе через эту точку 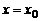 , то
, то 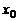 является экстремумом функции
является экстремумом функции 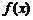 , причем:
, причем:
1)если 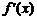 меняет свой знак с «+» на «–», то в точке
меняет свой знак с «+» на «–», то в точке 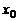 функция
функция  достигает максимум;
достигает максимум;
2)если 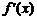 меняет свой знак с «–» на «+», то в точке
меняет свой знак с «–» на «+», то в точке 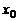 функция
функция  достигает минимум.
достигает минимум.
Теорема 10.4 (2-е достаточное условие экстремума). Если для дифференцируемой функции  в некоторой точке
в некоторой точке 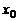 ее первая производная
ее первая производная 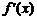 равна нулю, а вторая
равна нулю, а вторая 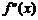 – существует и отлична от нуля, то есть
– существует и отлична от нуля, то есть
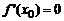 ,
, 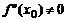 ,
,
то в этой точке функция  имеет экстремум, а именно:
имеет экстремум, а именно:
1)если 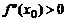 , то
, то 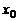 – минимум;
– минимум;
2)если 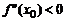 , то
, то 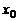 – максимум.
– максимум.
Наибольшее и наименьшее значения функции
Пусть функция  определена и непрерывна на отрезке
определена и непрерывна на отрезке 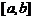 . Чтобы найти наибольшее (наименьшее) значение функции
. Чтобы найти наибольшее (наименьшее) значение функции  на отрезке
на отрезке 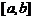 , необходимо перечислить все точки
, необходимо перечислить все точки 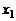 ,
, 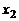 , …,
, …, 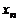 максимумов (минимумов), принадле-жащие интервалу
максимумов (минимумов), принадле-жащие интервалу 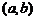 и выбрать наибольшее (наименьшее) значение из чисел
и выбрать наибольшее (наименьшее) значение из чисел 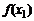 ,
, 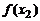 , …,
, …, 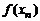 ,
, 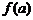 ,
, 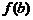 (рис. 10.3).
(рис. 10.3).
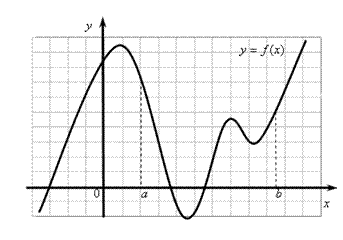
Рис. 10.3
Пример 10.1. Найти наибольшее и наименьшее значения функции 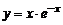 на отрезке
на отрезке 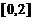 .
.
Решение.Найдем критические точки функции, для этого вычислим производную функции 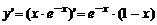 . Оп-ределим точки, в которых производная функции равна нулю:
. Оп-ределим точки, в которых производная функции равна нулю: 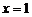 . Так как
. Так как 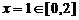 , то наибольшее и наименьшее зна-чения функции выберем из следующих:
, то наибольшее и наименьшее зна-чения функции выберем из следующих:
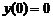 ;
; 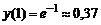 ;
; 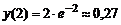 .
.
Ответ: 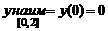 ,
, 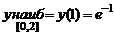 .
.
