ТЕМА 6. Кривые второго порядка

Рассмотрим плоскость 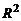. К кривым 2-го порядка относятся линии, описываемые многочленом от двух пере-менных, максимальная степень которого равна двум, то есть

,

.

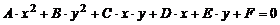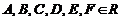Окружность

Окружностью называется геометрическое место точек плоскости, равноудаленных от некоторой фиксированной точки 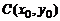, называемой ее центром.

Допустим, точка 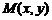лежит на данной окружности, то расстояние СМ равно некоторому числу R, называемому радиусом этой окружности: 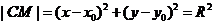– уравнение окружности с центром в точке 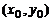и радиуса R.

Пример 6.1. Найти центр и радиус окружности .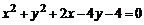

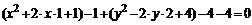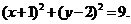Решение. Выделим полный квадрат по каждой перемен-ной, данное уравнение можно записать в виде: или Следовательно, это окружность с центром в точке 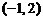и радиусом .

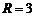Эллипс

Эллипсом называется геометрическое место точек плос-кости, для которых сумма расстояний до двух данных точек плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Выведем уравнение эллипса. Пусть 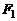и 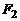– фокусы (рис. 6.1). Положим 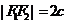. Декартову систему координат зададим следую-щим образом: ось Ox направим по прямой 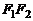, а начало поместим в середину отрезка 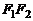. Тогда , .

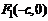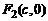Пусть 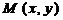– произвольная точка эллипса. Тогда 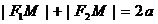, где величина a дана, причем 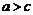. Имеем: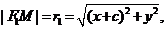

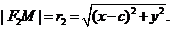
Следовательно, уравнение эллипса имеет вид:

.

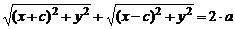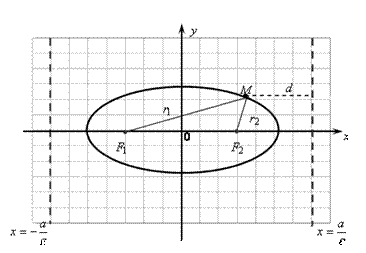
Рис. 6.1

Упростим последнее равенство: перенесем второе слагаемое в правую часть и возведем обе части в квадрат, получим 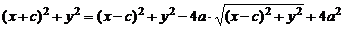, после раскрытия скобок и приведения подобных останется: 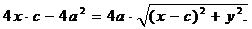Разделим полученное равенство на четыре, возведем обе части еще раз в квадрат: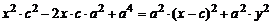

и преобразуем .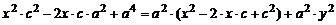

После приведения подобных получим:

, .

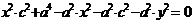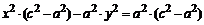Обозначим 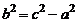и разделим обе части последнего равенства на эту величину: 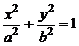– каноническое уравнение эллипса с полуосями 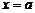, 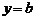и центром симметрии в точке 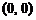. Число a в уравнении эллипса называется большой, а b – малой полуосью эллипса. Прямую, на которой расположены фокусы эллипса, называют фокальной осью.

Величина 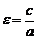называется эксцентриситетом эллипса, а прямые 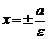называются директрисами эллипса.

Пример 6.2. Доказать, что уравнение 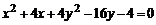определяет эллипс.

Решение. Преобразуем уравнение, выделив полные квадраты по каждой переменной, 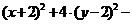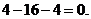Введем новые переменные 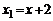, 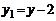. Тогда 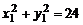или 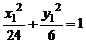. Последнее уравнение определяет эллипс с центром в точке 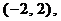причем , .

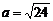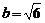Гипербола

Гиперболойназывается геометрическое множество точек плоскости, для которых абсолютная величина разности расстояний до двух данных точек 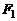и 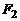этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Выведем уравнение гиперболы. Положим 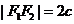. Систему координат (рис. 6.2) выберем так же, как и в случае эллипса. Тогд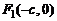а , а .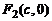

Если 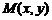– произвольная точка гиперболы, то 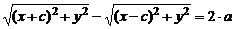, a – постоянная, 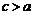. Это уравнение соответствует определению гиперболы. Преобразуя его, как и в случае эллипса, и положив 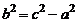, получим каноническое уравнение гиперболы:

.

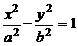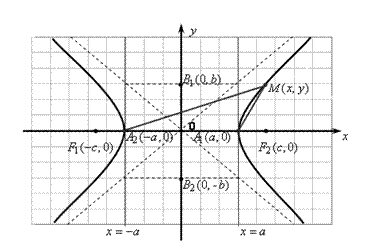
Рис. 6.2

Гипербола – кривая, симметричная относительно осей и начала координат. Прямые 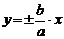являются асимптотами гиперболы, величина 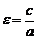называется эксцентриситетом гиперболы, 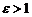, а прямые 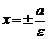– ее директрисами.

Парабола

Параболойназывается геометрическое место точек плоскос-ти, равноудаленных от данной точки F и данной прямой (рис. 6.3). Точка F называется фокусом параболы, а данная прямая – директрисой параболы. Для получения уравнения параболы выберем систему координат следующим образом: ось Ox проведем через фокус F перпендикулярно директрисе. Начало координат поместим в точку, равноудаленную от фокуса и директрисы. Обозначим расстояние между фокусом и директрисой через p. Величина p называется параметром параболы. В выбранной системе координат фокус F имеет координаты 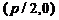, а уравнение директрисы имеет вид 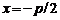или .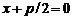

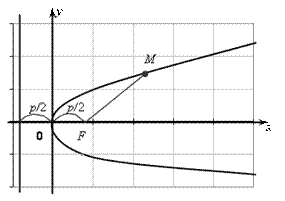
Рис. 6.3

Пусть 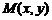– произвольная точка параболы. Соединим точку М с точкой F. Проведем отрезок MN перпендикулярно дирек-трисе. Согласно определению параболы, 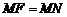. По формуле расстояния между двумя точками находим: 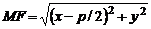, а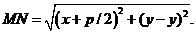

Следовательно, .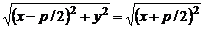

После элементарных преобразований получим каноническое уравнение параболы:

.

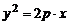Пример 6.3. Классифицировать линию 2-го порядка .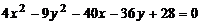

Решение. Воспользуемся формулой 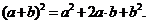Выделим полный квадрат по каждой переменной, для этого сгруппируем отдельно слагаемые, содержащие переменную x и y: 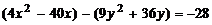. Коэффициенты при пере-менных в старшей степени вынесем общими множителями 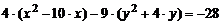. Полученные выражения в скобках доведем до полного квадрата, в первом случае прибавим и отнимем 25, во втором – 4: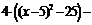 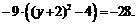После раскрытия скобок постоянные пе-ренесем в правую часть равенства 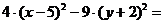= 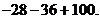Приведем подобные 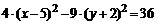. Запишем уравнение линии 2-го порядка в общем виде. Разделим последнее равенство на 36, чтобы получить единицу в правой части

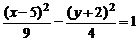или .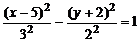

Данная линия (рис. 6.4) является гиперболой с центром в точке 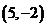и полуосями , .

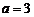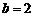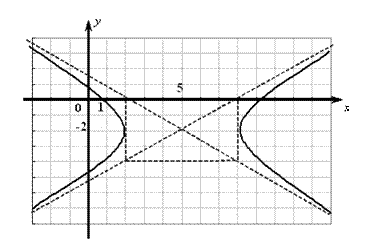
Рис. 6.4