Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную системы

Перевод чисел из двоичной системы в восьмеричную и шестнадцатеричную системы счисления можно выполнить двумя способами. Для реализации одного из них можно перевести двоичное число в десятичную систему счисления, а затем выполнить перевод десятичного числа в восьмеричную или шестнадцатеричную систему счисления.

Другой способ перевода более простой. Восьмеричная и шестнадцатеричная системы счисления являются системами, в основании которых лежит число 2 в третьей и в четвертой степени. Это обстоятельство позволяет переводить числа из двоичной системы в восьмеричную и шестнадцатеричную системы следующим образом.

Для перевода в восьмеричную систему двоичное число делят на триады и с помощью таблицы (табл.1) ставят в соответствие каждой триаде восьмеричную цифру.

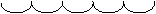10.001.110.111.010₂=21672₈

2 1 6 7 2

Чтобы перевести в шестнадцатеричную систему двоичное число надо разделить его на тетрады и с помощью таблицы поставить в соответствие каждой тетраде шестнадцатеричную цифру.

1.0101.0101.1011.1010₂ =155ВА₁₆

1 5 5 В А

Числа в разных системах счисления. Таблица 1

Двоичные числа	Восьмеричные числа	Десятеричные числа	Шестнадцатеричные числа
			А
			В
			С
			D
			E
			F

Примеры

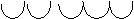100.111.011.010.101₂=47325₈

4 7 3 2 5

1001.1101.1100.1010.1111₂ =9DCAF ₁₆

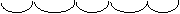9 D C A F

Перевод дробных чисел из десятичной системы счисления в двоичную, восьмеричную, шестнадцатеричную системы счисления

Перевод десятичных дробей можно выполнять по следующему правилу:

Дробную часть числа нужно умножать на основании новой системы счисления и выписывать целую часть произведения, получившуюся при умножении дробную часть опять умножать на новое основание до тех пор, пока дробная часть не превратится в ноль или не обнаружится период.

Для удобства вычислений, проводится вертикальная черта, отделяющая дробную часть от целой и действия выполняются столбиком.

Разбор заданий

А₁₀ = 0,28125 А₂ -?, А₈ -?, А₁₆-?.

0,ê28125 0,ê28125 0,ê28125

ê 2 ê 8 ê 16

0ê56250 2ê25000 4ê5

ê 2 ê 8 ê16

1ê1250 2ê00 8ê00

ê 2

0ê250

ê 2

0ê50

ê2

1ê0

А₂ = 0,01001 А₈ = 0,22 А₁₆ = 0,48.

А₁₀ = 0,325 А₈ -?.

0,ê325

ê 8

2ê600

ê8

Þ 4ê8

ê8

6ê4

ê8

3ê2

ê8

1ê6

ê8

Þ 4ê8

А₈ = 0,2(4631) - циклическая дробь.

Если дробь содержит целую часть, то дробная и целая части переводятся отдельно по своим правилам.

А10 = 43,125 А2 -?,

Сначала переводим целую Затем переводим дробную часть:

часть дроби:

0,ê125

ê 2

0ê250

ê 2

0ê50

ê2

1ê0

0.125₁₀ = 0.001₂.

43 ë2_

42 21 ë2_

1 20 10 ë2_

ã 1 10 5 ë2_

ã 0 4 2 ë2_

ã 1 2 1

ã 0 å

43₁₀ = 101011₂.

После нахождения целой и дробной части соединяем их вместе: А2 = 101011.001

Перевод обыкновенных правильных дробей выполняют по следующему правилу:

Числитель правильной дроби нужно разложить на слагаемые, которые являются степенями основания новой системы счисления, представить дробь в виде суммы дробей, затем сократить эти слагаемые и записать числители слагаемых дробей в позицию числа, соответствующую степени знаменателя.

Разбор заданий

Дана правильная дробь 29/32. Представьте ее в двоичной системе счисления.

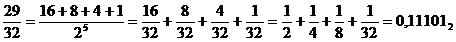Дана дробь 60/64. Перевести ее в восьмеричную и шестнадцатеричную системы счисления:

а) Переведем дробь в двоичную систему счисления

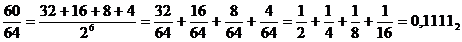б) Переведем дробь в восьмеричную систему счисления путем разбиения двоичного числа на триады:

0,111 1002=0,748

в) Переведем дробь в шестнадцатеричную систему счисления путем разбиения двоичного числа на тетрады: 0,1111 2=0,F16