Основные свойства степенных рядов

Можно показать, что степенной ряд 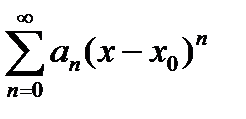имеет равномерную сходимость при всех х, таких, что 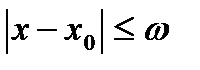, где .

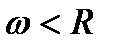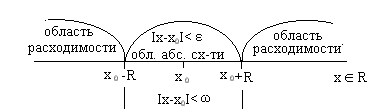
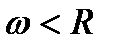
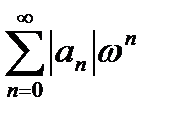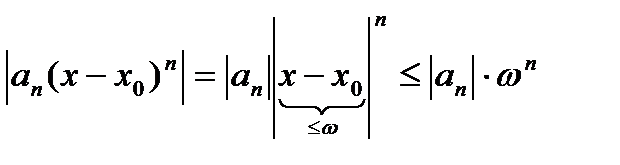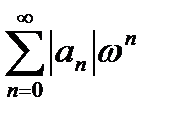Мажорантом при этом является числовой ряд , так как и ряд сходится, так как точка 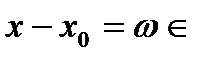области абсолютной сходимости исходного ряда.

Таким образом, степенной ряд сходится равномерно на любом отрезке, полностью лежащем внутри области абсолютной сходимости.

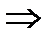Для всех х из области абсолютной сходимости для степенных рядов выполняются свойства, общие для всех равномерно сходящихся рядов:

1. Сумма степенного ряда является непрерывной функцией для 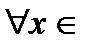области равномерной сходимости

2. Степенной ряд можно в области равномерной сходимости можно почленно дифференцировать и интегрировать, при этом дифференцируется и интегрируется его сумма, а R не изменяется(на концах промежутка при этом возможно изменение характера сходимости).

Ряды Тейлора и Маклорена.

Рассматриваем функцию - дифференцируемая сколько угодно раз в точке и некоторой ее окрестности .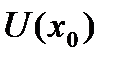

Рядом Тейлора для функции в точке называется следующий числовой ряд:

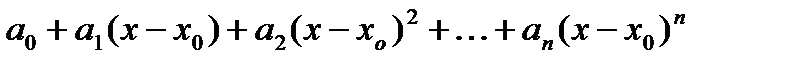, (1)

в котором коэффициенты 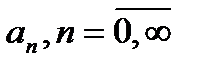вычислены через функцию по следующим формулам:

,

,

.

…

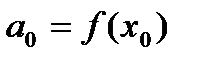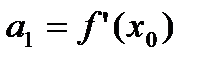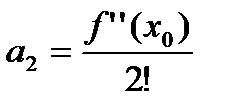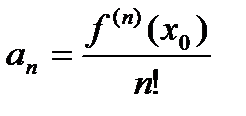
Рядом Маклорена для функции называется частный случай ее ряда Тейлора в точке =0:

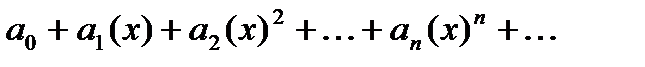(2)

,

,

.

…

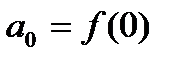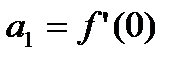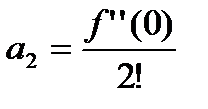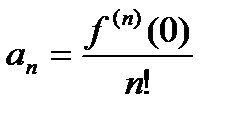
Название для рядов (1) и (2) сохраняются независимо от их сходимости/расходимости и даже в случае, если ряды сходятся не к функции .

Если ряд Тейлора (Маклорена) сходится в некоторой области к функции , то справедливо равенство:

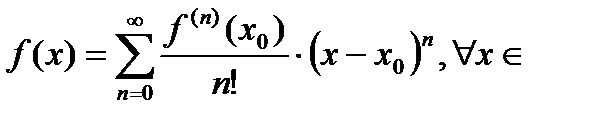области сходимости ряда Тейлора. (3)

В этом случае это равенство называется разложением функции в ряд Тейлора в точке .

Замечание: так как ряд Тейлора – это есть степенной ряд по степеням 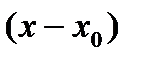, его область сходимости записывается неравенством 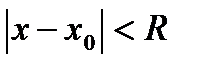, R – радиус сходимости. Так как это неравенство описывает 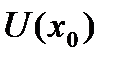, то разложение функции в ее ряд Тейлора справедливо в точке и некоторой ее окрестности .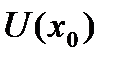

Пример:

Составить разложение функции 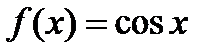в ряд Тейлора в точке 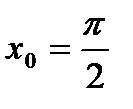. Найти окрестность 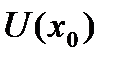, в которой составленный ряд находится.

Решение:

Хотим получить следующее разложение:

,

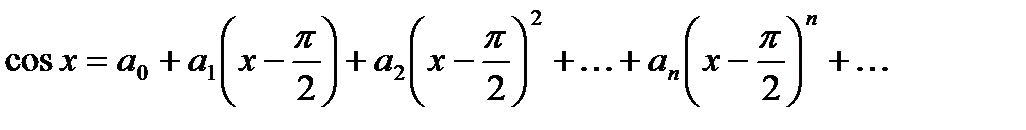где .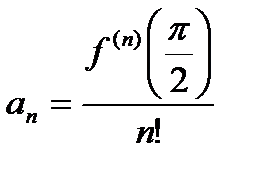

Разложение должно быть верно по окрестности 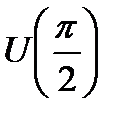, т.е. при .

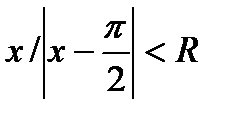1. Вычислим коэффициенты Тейлора:

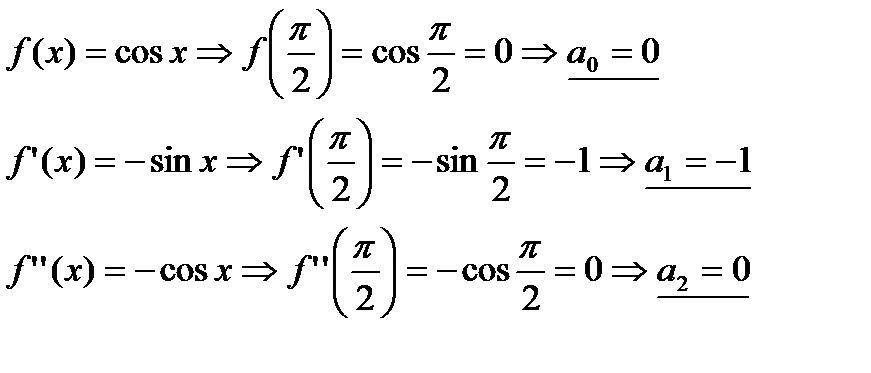
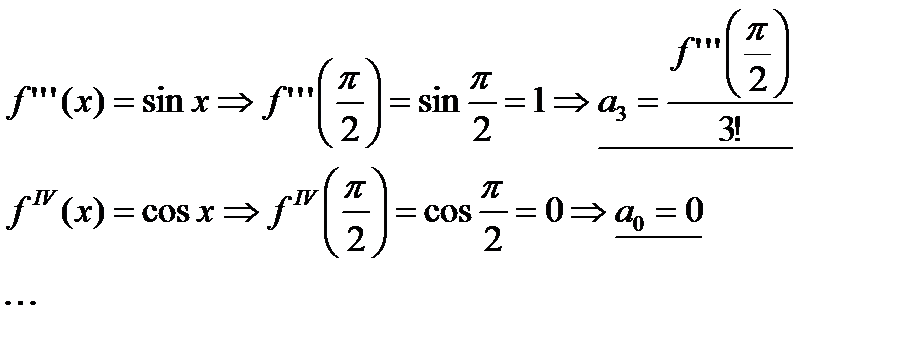
Составляем ряд Тейлора:

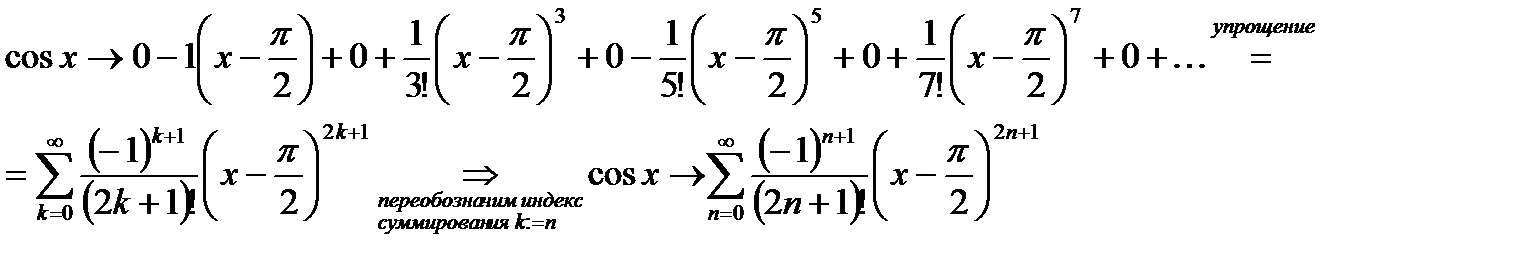
2. Зная, что составленный степенной ряд сходится абсолютно при 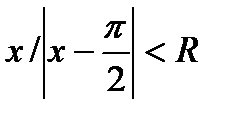, вычислим R, применяя признак Даламбера к ряду из модулей:

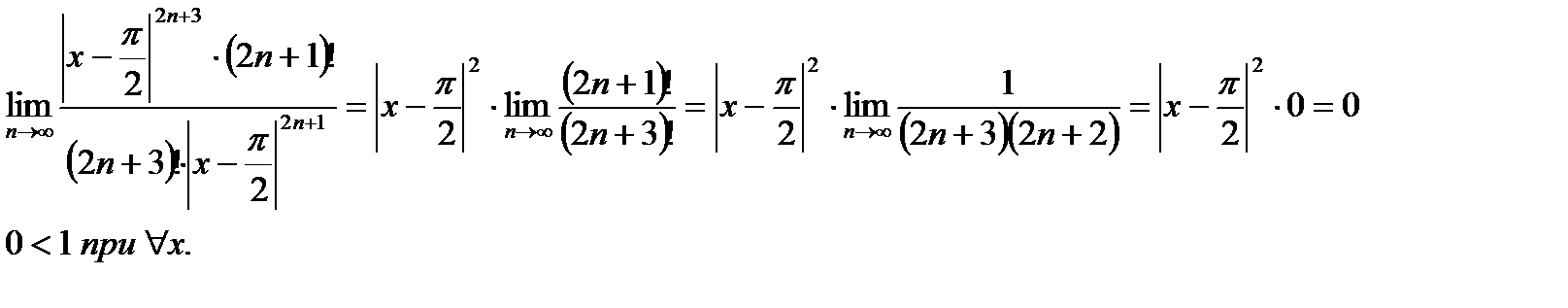
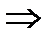составленный степенной ряд сходится при 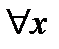и его .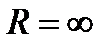

3. Составленный ряд сходится при 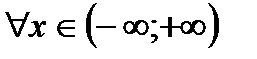, но остается недоказанным, что его сумма .

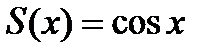Поэтому ответ по задаче остается неполным.

Ответ: 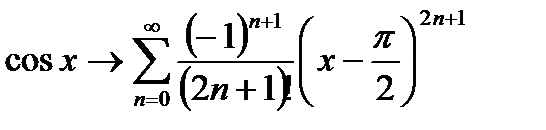сходится абсолютно при .

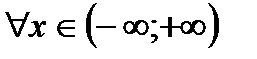Остаточный член ряда Тейлора в форме Лагранжа:

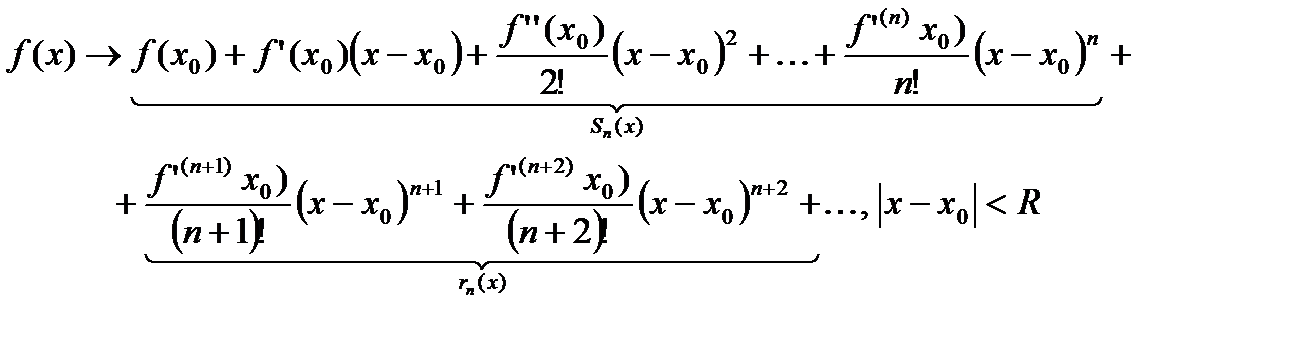
Можно показать, что:

1. Остаток ряда Тейлора записывается в нескольких конечных формах, наиболее распространенной из этих форм является форма Лагранжа:

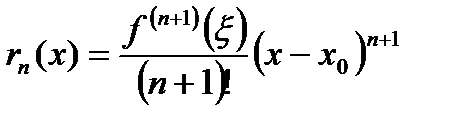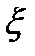, где - некоторая фиксированная точка между точкой и точкой х.

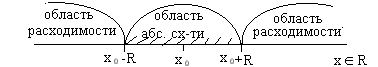
2R

2. Достаточным условием для того, чтобы составленный ряд Тейлора сходился именно к той функции, для которой он составлялся, является услови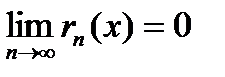е , где 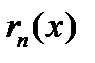записано в форме Лагранжа.

Пример:

,

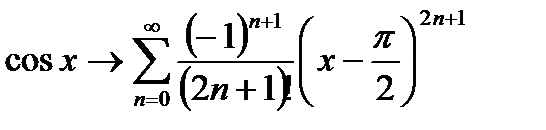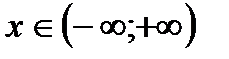
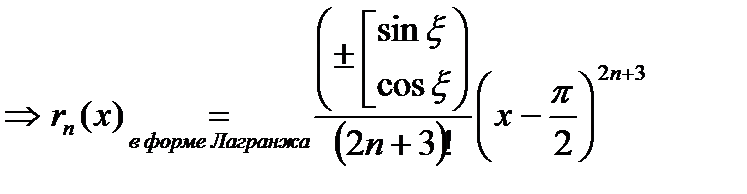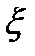, где - некоторая фиксированная точка слева или справа от (между х и ).

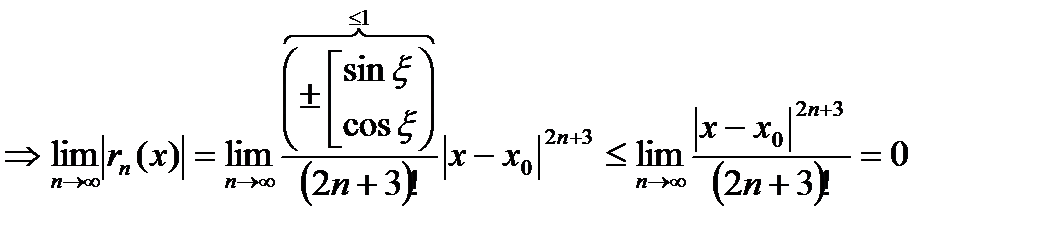, так как 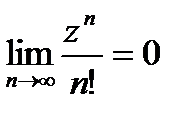при 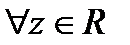, т.е. степенная функция с любым основанием при увеличении ее основания растет медленнее, чем факторная ее показателя (будет обосновано позже).

Таким образом, 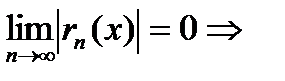ряд сходится,

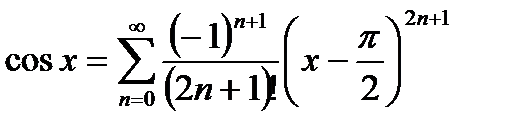- это равенство называется разложением 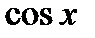в ряд Тейлора в точке 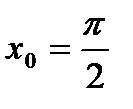(или по степени ).

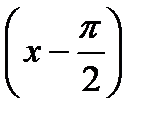Замечания к разложениям функций в ряды Тейлора:

1. Необходимым условием для разложения функции в ряд Тейлора является существование и непрерывность в точке и 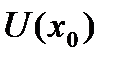производных любого порядка, т.е. функция должна быть непрерывно дифференцируемой бесконечное количество раз в точке и .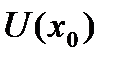

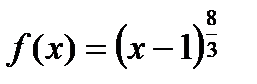- такую функцию в точке 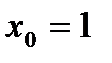в ряд Тейлора разложить нельзя, так как 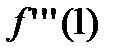не 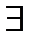( но в точке 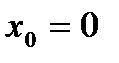и других точках - можно)

разложение функции в степенной ряд в точке это локальная процедура, так как она выполняется только по некоторой окрестности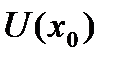

2. Если в точке разлагается в степенной ряд, то это разложение является единственным и совпадает с ее разложением в ряд Маклорена.

Доказательство:

Пусть имеет разложение в ряд по степеням :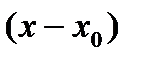

,

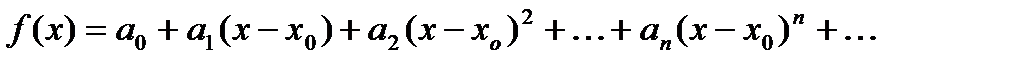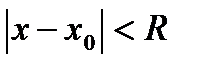
Это равенство справедливо при всех х из промежутка сходимости, следовательно, справедливо 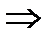при , при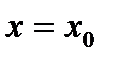

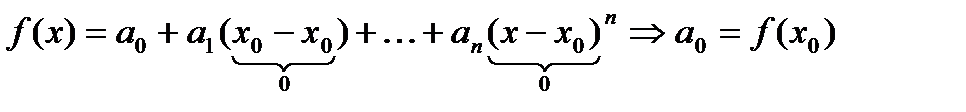
Так как степенные ряды можно почленно дифференцировать, то справедливо равенство:

,

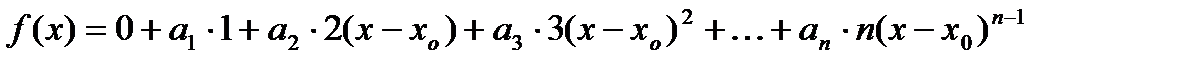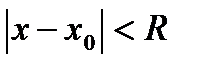
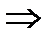при .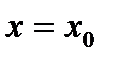

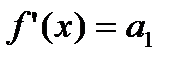Аналогично, повторяя дифференцирование разложения в ряд и полагая 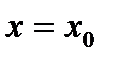, получим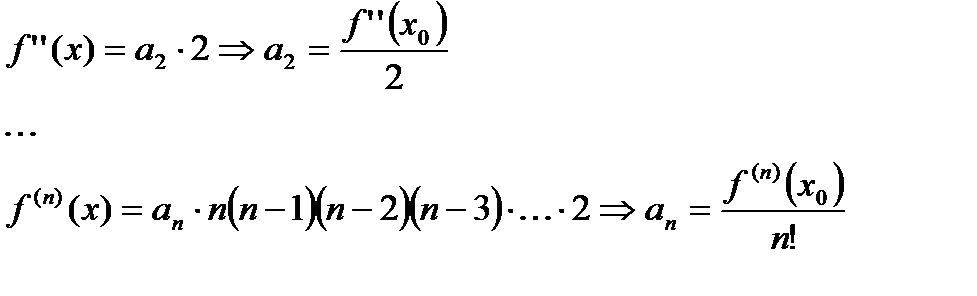

Для произвольно взятого разложения функции в степенной ряд доказали, что его коэффициенты неизбежно совпадают с коэффициентами Тейлора 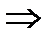разложение в степенной ряд единственно и совпадает с разложением Тейлора.

3. Достаточным условием для того, чтобы ряд Тейлора сходился к является условие:

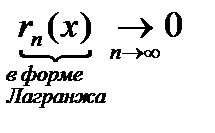
Обоснование этого факта для конкретной функции является, как правило, затруднительным, поэтому в приложениях стараются получить разложение функции в степенной ряд, используя так называемые стандартные разложения в ряд Маклорена некоторых элементарных функций. При этом и промежуток сходимости и сумма ряда получаются автоматически.