Числовые характеристики дискретных случайных величин
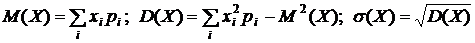 (8)
(8)
Биномиальное распределение
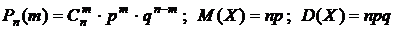 (9)
(9)
Распределение Пуассона
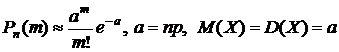 (10)
(10)
Непрерывные случайные величины:
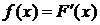 (11)
(11)
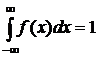 (12)
(12)
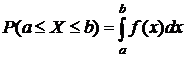 (13)
(13)
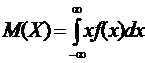 (14)
(14)
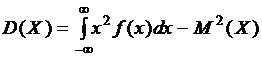 (15)
(15)
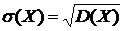 (16)
(16)
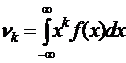 (17)
(17)
Показательное распределение
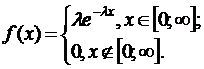 ;
; 
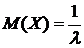 ;
; 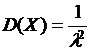 ; (18)
; (18) 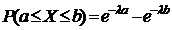 , если
, если 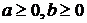
Равномерное распределение
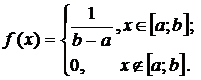 ;
; 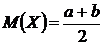 ;
; 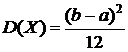 (19)
(19)
Нормальное распределение
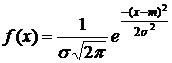 ;
; 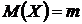 ;
; 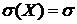 ;
; 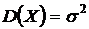 (20)
(20)
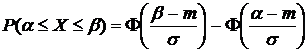
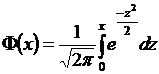 (21)
(21)
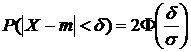 (22)
(22)
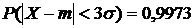 (23)
(23)
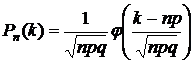 , где
, где 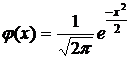 (24)
(24)
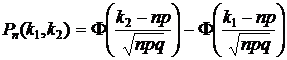 (25)
(25)
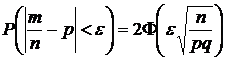 (26)
(26)
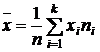 , где
, где 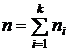 (27)
(27)
Доверительный интервал для математического ожидания:
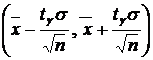
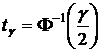 , или
, или 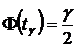 (28)
(28)
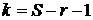 (29)
(29)
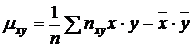 (30)
(30)
 (31)
(31)
 (32)
(32)
СЛОВАРЬ ОСНОВНЫХ ПОНЯТИЙ
Достоверное, недостоверное, случайные и несовместимые события.
Достоверным называют событие, которое обязательно произойдёт, если будет осуществлена определенная совокупность условий.
Недостоверное или невозможное событие, которое заведомо не произойдёт, если будет осуществлена совокупность событий.
Случайное событие при осуществлении совокупности событий может либо произойти, либо не произойти.
События называют несовместными, если появление одного из них исключает появление двух других событий в одном и том же испытании
Классическое определение вероятности.
Вероятность - одно из основных понятий теории вероятностей. Существует несколько определений этого понятия. Приведем определение, которое называют классическим.
Рассмотрим пример. Пусть в урне содержится 6 одинаковых, тщательно перемешанных шаров, причем 2 из них - красные, 3 - синие и 1 - белый. Очевидно, возможность вынуть наудачу из урны цветной (т. е. красный или синий) шар больше, чем возможность извлечь белый шар. Можно ли охарактеризовать эту возможность числом? Оказывается, можно. Это число и называют вероятностью события (появления цветного шара). Таким образом, вероятность есть число, характеризующее степень возможности появления события.
Вероятность события A это - 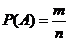
Элементарные исходы.
В формулах обозначается буквой n. Исходы = испытания.
Перестановки.
Комбинации, состоящие из одних и тех же «n» различных элементов и отличающиеся порядком их расположения. Число всех возможных перестановок 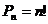
Размещения.
Это комбинации из «n» различных элементов, которые отличаются либо составом элементов, либо их порядком.
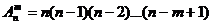
Сочетания.
Это комбинации, составленные из “n” различных элементов по “m” элементов, которые отличаются хотя бы одним элементом.
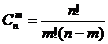
Относительная частота.
Это отношение числа испытаний, в которых событие появилось, к общему числу фактически произведённых испытаний.
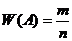 m – число появления события, n – общее число испытаний.
m – число появления события, n – общее число испытаний.
Полная группа событий. Равновозможные события.
Сумма вероятностей A1,A2,…,An, образуют полную группу
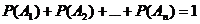
Противоположные события.
Это два единственно возможных события образующих полную группу
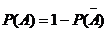
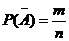
Сумма двух событий.
Суммой A+B двух событий A и B называют событие, состоящее в появление события A, или события B, или обоих этих событий.
Например, если из орудия произведены 2 выстрела и событие A означает попадание при первом выстреле, событие B — попадание при втором выстреле, то A+B - попадание при 1 -м выстреле или при 2-м.
В частности, если два события A и B - несовместные, то A+B - событие, состоящее из появления одного из этих событий, безразлично какого.
Сумма нескольких событий.
Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий.
Например, событие A+B+C состоит в появлении одного из следующих событий: А;B;С;A и B,A и C;B и C;A и B и С.
Произведение двух событий.
Произведением двух событий A и B называют событие AB, состоящее в совместном появлении этих событий.
Если событие A состоит в том, что вынутая деталь годная, а событие B - окрашенная, то событие AB, означает, что деталь и годная и окрашенная.
