Геометрическое определение вероятности события

Геометрическое определение вероятности является обобщением классического определения на случай, когда число равновозможных исходов бесконечно.

Геометрической вероятностью события А называется отношение меры области, благоприятствующей появлению события А, к мере всей области, т.е.

,

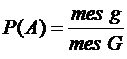где mes G — мера множества возможных исходов (длина отрезка, площадь или объем области), а mes g —мера множества благоприятных исходов.

Пример 1.4.1.В круг наудачу брошена точка. Найти вероятность того, что она не попадет в правильный треугольник, вписанный в этот круг.

Решение.В этом случае мерой множества возможных исходов является площадь круга: S=p×R², а мерой множества благоприятных исходов — разность площадей круга и треугольника: 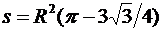. Следовательно, вероятность заданного события равна

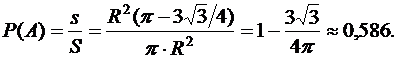
Задачи

1.24. Точка брошена в круг радиуса R. Найдите вероятность того, что она попадает внутрь данного вписанного квадрата.

(Ответ: .)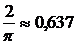

1.25. В квадрат с вершинами в точках (0,0), (0,1), (1,1), (1,0) наудачу брошена точка. Найдите вероятность того, что координаты этой точки удовлетворяют неравенству y < 2x.

(Ответ: 0,75.)

1.26. Расстояние от пункта А до пункта В автобус проходит за 2 мин, а пешеход – за 15 мин. Интервал движения автобусов 25 мин. Вы подходите в случайный момент времени к пункту А и отправляетесь в пункт В пешком. Найдите вероятность того, что в пути вас догонит очередной автобус.

(Ответ: 0,52.)

1.27. Два парохода должны подойти к одному и тому же причалу. Время прихода обоих пароходов равновозможно в течение данных суток. Найдите вероятность того, что одному из пароходов придется ждать освобождения причала, если время стоянки первого парохода 1 ч, а второго – 2 ч.

(Ответ: 0,121.)

1.28. В прямоугольник со сторонами 1 и 2 брошена точка А. Найдите вероятности следующих событий: а) расстояние от точки А до ближайшей стороны прямоугольника не превосходит х; б) расстояние от точки А до любой стороны прямоугольника не превосходит х; в) расстояние от точки А до ближайшей диагонали прямоугольника не превосходит х.

(Ответ: а) 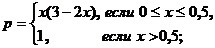б)

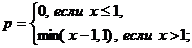
в) .)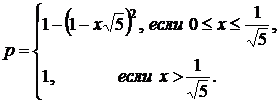

1.29. В квадрат со стороной а брошена точка А. Найдите вероятность того, что расстояние от точки А до ближайшей стороны квадрата меньше, чем расстояние от А до ближайшей диагонали.

(Ответ: )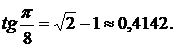

Элементы комбинаторики

Очень часто непосредственный перебор всех возможных исходов опыта затруднителен в силу их большого количества. Для решения таких задач полезно использовать некоторые комбинаторные формулы.

Пусть А_i (i = 1,2,...,n) — элементы конечного множества.

Правило суммы. Если элемент А₁может быть выбран п₁ способами, элемент А₂— другими п₂способами, А₃ — отличными от первых двух п₃ способами и т.д., А_k — п_k способами, отличными от первых (k – 1) способов, то выбор одного из элементов: или А₁,или А₂,...,или А_k может быть осуществлен п₁+п₂+…+ п_k способами.

Правило произведения. Если элемент А₁может быть выбран п₁ способами, после такого выбора элемент А₂ может быть выбран п₂ способами и т.д., после каждого (k – 1) выбора элемент А_k может быть выбран п_k способами, то выбор всех элементов А₁, А₂,..., А_k в указанном порядке может быть осуществлен п₁´п₂´...´п_k способами.

Виды комбинаций

Пусть дано множество из п различных элементов. Из этого множества могут быть образованы подмножества из т элементов ( ).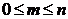

Размещением из п элементов по т называется любое упорядоченное подмножество из т элементов множества, состоящего из п различных элементов, т.е. комбинации из n элементов по m отличаются либо составом элементов, либо порядком их расположения (либо и тем, и другим). Число размещений определяется по формуле

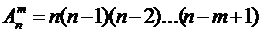или .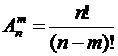

Пример 1.5.1. Сколько двузначных чисел можно составить из трех цифр 3, 5, 7?

Решение. Каждый вариант чисел представляет набор 2 цифр из 3, отличающийся от других вариантов как составом цифр, так и порядком их следования, т.е. является размещением из 3 элементов по 2. Число вариантов чисел, т.е. число размещений из 3 по 2, находим по формуле:

.

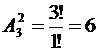Сочетанием из п элементов по т любое подмножество из т элементов множества, состоящего из п различных элементов, то есть комбинации из n элементов по т отличаются только составом элементов. Число сочетаний из п элементов по т:

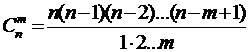или .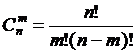

Свойства числа сочетаний:

, ; ;

; .

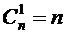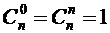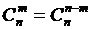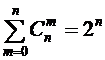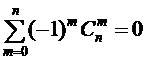Пример 1.5.2. Сколько различных произведений из двух цифр можно составить, используя цифры 3, 5, 7.

Решение. Каждое произведение чисел представляет набор двух цифр из трёх, отличающийся от других только составом пар, то есть представляет собой сочетание двух цифр из трёх. Число вариантов произведения равно:

.

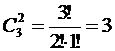Перестановкой из п элементов называется любое упорядоченное множество, в которое входят по одному разу все п различных элементов данного множества, то есть комбинации из п элементов отличаются только порядком расположения этих элементов. Число перестановок из п элементов определяется по формуле:

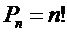
Пример 1.5.3.Сколько четырехзначных чисел можно составить из цифр 1, 2, 3, 4, если каждая цифра входит в изображение числа только один раз?

Решение. Каждый вариант комбинации четырех чисел отличается только порядком расположения этих чисел, то есть является перестановкой из четырех чисел. Их число определяется по формуле:

.

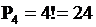Если в размещениях (сочетаниях) из п элементов по т некоторые из элементов (или все) могут оказаться одинаковыми, то такие размещения (сочетания) называют размещениями (сочетаниями) с повторениями.

Число размещений с повторениями определяется по формуле:

,

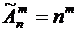а число сочетаний с повторениями определяется по формуле: .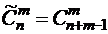

Пример 1.5.4. В конкурсе участвуют 7 участников по двум номинациям. Сколько существует вариантов распределения призов, если по каждой номинации установлены: а) различные призы; б) одинаковые призы?

Решение. а) Каждый вариант распределения призов представляет собой комбинацию 2 призов среди 7 участников, отличающуюся от других комбинаций как составом участников, так и порядком их номинирования, причем одни и те же участники могут повторяться, т.е. представляет собой размещение с повторениями из 7 элементов по 2. Их число по формуле:

.

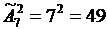б) Если по каждой номинации установлены одинаковые призы, то порядок следования участников не имеет значения, а число вариантов распределения призов представляет собой число сочетаний с повторениями из 7 участников по 2:

.

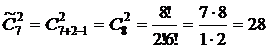Если в перестановках из общего числа п элементов есть k различных элементов, при этом первый элемент повторяется n₁ раз, 2-й элемент – n₂ раз, k-й элемент – n_k раз, причем n₁+n₂+…+n_k = п, то такие перестановки называют перестановками с повторениями из п элементов. Число перестановок с повторениями из п элементов определяется по формуле

.

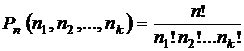Пример 1.5.5. Сколько существует пятизначных чисел, составленных из цифр 1, 2 и 3, в которых цифра 1 встречается 1 раз, а цифры 2 и 3 – по 2 раза?

Решение. Каждое пятизначное число отличается от другого порядком следования цифр (причем n₁+ n₂+ n₃=5), т.е. представляет собой перестановки с повторениями из 5 элементов. Их число по формуле:

.

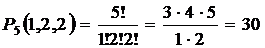Пример 1.5.6. В группе 25 студентов. Вызываются во время занятия 3 студента. Полагая, что вызов производится случайно, определить, какова вероятность того, что будут вызваны данные 3 студента в определенном порядке (событие А).

Решение. В качестве одного исхода будем считать вызов любых трёх студентов в определённом порядке. Таким образом, каждый исход представляет собой размещение по 3 элемента из 25. Всего таких исходов будет 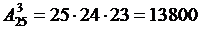, среди них благоприятствующий исход 1. Следовательно,

.

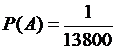Пример 1.5.7. 10 человек садятся случайным образом за круглый стол. Найти вероятность того, что два определённых лица окажутся рядом.

Решение. Общее число всех возможных исходов n = 10!. Два выбранных лица могут сесть рядом двадцатью способами (т.е. первый может выбрать себе место десятью способами, тогда второй может сесть либо слева, либо справа от него). Оставшиеся 8 мест могут быть распределены среди остальных лиц числом способов, равным 8!. Поэтому m = 20·8!

.

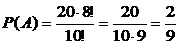Пример 1.5.8. Собрание, на котором присутствуют 25 человек, в том числе 5 женщин, выбирает делегацию из 3 человек. Считая, что каждый из присутствующих с одинаковой вероятностью может быть избран, найти вероятность того, что в делегацию войдут две женщины и один мужчина (событие А).

Решение. Общее число всех возможных исходов — это число сочетаний из 25 человек по 3, т.е. n = 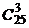. Число исходов благоприятствующих событию А, найдем как произведение числа сочетаний из 5 женщин по 2 и числа сочетаний из 20 мужчин по 1, т.е. 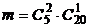. Тогда

.

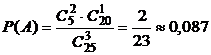Задачи

1.30. Имеется 5 видов конвертов без марок и 4 вида марок одинаковой стоимости. Сколькими способами можно выбрать конверт с маркой для посылки письма?

(Ответ: 20.)

1.31. Сколько словарей надо издать, чтобы можно было непосредственно выполнить переводы с любого из 5 языков: русского, английского, французского, немецкого, итальянского – на любой другой из этих 5 языков?

(Ответ: 20.)

1.32. У одного студента 5 книг, у другого – 9. Все книги различные. Сколькими способами студенты могут произвести обмен: а) одной книги на книгу? б) 2 книги на 2 книги?

(Ответ: а) 45; б) 360.)

1.33.На вершину горы ведут 5 тропинок. Сколькими способами турист может подняться в гору и потом спуститься с нее? Решите эту задачу с дополнительным условием: подъем и спуск должны происходить по разным тропинкам.

(Ответ: 25; 20.)

1.34. Сколькими способами на шахматной доске можно указать: а) 2 клетки; б) 2 клетки одного цвета; в) 2 клетки разного цвета?

(Ответ: а) 2016; б) 992; в) 1024.)

1.35. Имеются 3 письма, каждое из которых можно послать по 6 различным адресам. Сколькими способами можно осуществить рассылку писем, если: а) никакие 2 письма не посылать по одному адресу; б) по одному можно адресу посылать более одного письма.

(Ответ: а) 120; б) 216.)

1.36. В пассажирском поезде 9 вагонов. Сколькими способами можно рассадить в поезде 4 человек при условии, что все они должны ехать в различных вагонах?

(Ответ: 3024.)

1.37. Из цифр 1, 2, 3, 4, 5 составляются всевозможные числа, каждое из которых состоит не более чем из 3 цифр. Сколько таких чисел можно составить, если: а) повторение цифр в числах не разрешается; б) разрешается повторение цифр?

(Ответ: а) 85; б) 155.)

1.38. Сколькими способами 3 различных подарка А, В и С можно сделать каким-то 3 из 15 лиц, если: а) никто не должен получать более одного подарка; б) подарок А должно получить определенное лицо?

(Ответ: а) 2730; б) 182.)

1.39. В группе 9 человек. Сколько можно образовать разных подгрупп при условии, что в подгруппу входит не менее 2 человек?

(Ответ: 502.)

1.40. Сколько существует различных автомобильных номеров, которые состоят из пяти цифр, если первая цифра не равна нулю?

(Ответ: 90000.)

1.41. Сколькими способами можно расставить на полке семь различных книг, если: а) две определенные книги должны стоять рядом; б) эти две книги не должны стоять рядом?

(Ответ: а) 1440; б) 3600.)

1.42. Группу из 20 студентов нужно разделить на 3 бригады, причем в первую бригаду должны входить 3 человека, во вторую – 5 и в третью – 12. Сколькими способами это можно сделать?

(Ответ: .)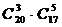

1.43. Для участия в команде тренер отбирает пять мальчиков из десяти. Сколькими способами он может сформировать команду, если два определенных мальчика должны войти в команду?

(Ответ: 56.)

1.44. В течение четырех недель студенты сдают четыре экзамена, в том числе два экзамена по математике. Сколькими способами можно распределить экзамены по неделям так, чтобы экзамены по математике не следовали один за другим?

(Ответ: 12.)

1.45.Восемь человек должны сесть в два автомобиля, причем в каждом должно быть по крайней мере три человека. Сколькими способами они могут это сделать?

(Ответ: 182.)

1.46. Сколько различных слов можно получить из всех букв слова «перестановка»?

(Ответ: 119750400.)

1.47. Сколько различных чисел можно получить, переставляя цифры числа 2 233 344 455?

(Ответ: 25200.)

1.48. Имеется 20 наименований товаров. Сколькими способами их можно распределить по трем магазинам, если известно, что в первый магазин должно быть доставлено восемь наименований, во второй – семь наименований и в третий – пять наименований товаров?

(Ответ: .)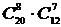

1.49. В вазе стоят 9 красных и 7 белых гвоздик. Сколькими способами можно выбрать из нее а) 3 гвоздики; б) 6 гвоздик одного цвета; в) 4 красных и 3 белых гвоздики?

1.50. Сколькими способами могут быть распределены три призовых места среди 16 соревнующихся?

1.51. В студенческой группе 12 девушек и 16 юношей. Сколькими способами можно выбрать двух студентов одного пола?

1.52. Сколько чисел, содержащих не менее трех попарно различных цифр, можно составить из цифр 2, 4, 6, 8, 9?

1.53. Если подбросить одновременно три игральные кости, то сколько имеется различных возможных комбинаций выброшенных очков?

1.54. Из отряда солдат в 50 человек, среди которых есть рядовой Иванов, назначаются в караул 4 человека. Сколькими способами может быть составлен караул? В скольких случаях в число караульных попадет рядовой Иванов?

1.55. В цветочном магазине 7 видов цветов. Сколькими различными способами можно составить букет, содержащий 3 цветка?

1.56. Сколько различных трехзначных чисел можно составить из цифр 0, 2, 3, 5, 7, если: а) цифры не повторяются; б) цифры могут повторяться?

1.57. Сколькими способами 3 награды могут быть распределены между 10 участниками соревнования?

1.58. Сколькими способами можно составить трехцветный полосатый флаг (три горизонтальные полосы), если имеется материал 5 различных цветов?

1.59. Сколькими способами можно расставить на книжной полке 10-ти томное собрание сочинений, располагая их: а) в произвольном порядке; б) так, чтобы I, V и IX тома стояли рядом (в любом порядке); в) так, чтобы I, II и III тома не стояли рядом (в любом порядке);

1.60. В комнате имеется 7 стульев. Сколькими способами можно разместить на них 7 гостей? 3 гостя?

1.61. Студенты сдают 5 экзаменов, в том числе 2 экзамена по математике. Сколькими способами можно распределить экзамены, но так, чтобы экзамены по математике следовали один за другим? Не следовали один за другим?

1.62. Владимир хочет пригласить в гости троих из семи своих лучших друзей. Сколькими способами он может выбрать приглашенных?

1.63. Сколькими способами можно разбить 8 предметов на две равные по количеству предметов группы?

1.64. Пять авторов должны написать задачник по математике, состоящий из 14 глав. Два автора напишут по 2 главы, два других – по 3 и еще один – 4 главы книги. Сколькими способами может быть распределен материал между авторами?

1.65. В ящике 15 деталей, среди которых 6 бракованных. Наудачу выбирается комплект из 5 деталей. Сколько всего комплектов, в каждом из которых 2 детали бракованные?

1.66. Пять человек вошли в лифт на первом этаже 9-ти этажного дома. Сколькими различными способами пассажиры могут выйти из лифта на нужном этаже? На восьмом этаже?

1.67. Встретившись перед занятиями 25 студентов, обменялись рукопожатиями. Сколько всего было сделано рукопожатий?

1.68. Из состава конференции, на которой присутствуют 52 человека, надо избрать счетную комиссию, состоящую из 5 человек. 1) Сколькими способами это можно сделать? 2) Предположим, что в состав делегатов конференции входит Петров. Сколько существует способов выбора комиссии, при которых Петров входит в состав комиссии? 3) Сколько существует способов выбора комиссии, при которых Петров не входит в состав комиссии?

1.69. Сколько аккордов можно взять на 10 выбранных клавишах рояля, если каждый аккорд может содержать от 3 до 10 звуков?

1.70. В гостиницу прибыли 12 человек, в которой есть один четырехместный, два трехместных и один двухместный номера. Сколько существует способов их размещения?