Образец выполнения контрольной работы №10.

Задание 1.

В партии из 20 изделий 6 изделий имеют скрытый дефект. Какова вероятность того, что из взятых наугад 3 изделий 2 изделия являются дефектными.

Решение:

I способ.

Воспользуемся формулой

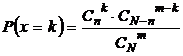, где

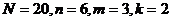
Имеем .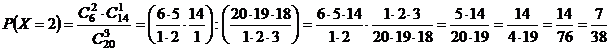

II способ.

Всего исходов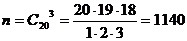

Число благоприятных исходов

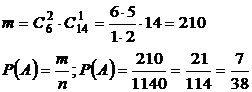
Ответ: .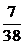

Задание 2.

В магазине выставлены для продажи 15 изделий, среди которых 6 изделий некачественные. Какова вероятность того, что взятые случайным образом 3 изделия будут качественными.

Решение:

I способ.

Событие А – первое изделие некачественное, тогда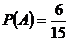

Событие В – второе изделие некачественное,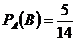

Событие С – третье изделие некачественное, .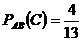

Тогда по правилу умножения имеем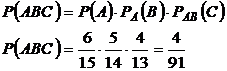

II способ.

Всего исходов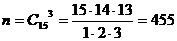

Число благоприятных исходов

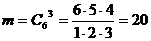, имеем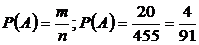

Ответ: .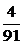

Задание 3.

На сборочное предприятие поступили изделия с трех заводов в количестве: с первого – 10, со второго - 40, с третьего – 50. Вероятность качественного изготовления изделий на первом заводе – 0,7, на втором – 0,6 , на третьем – 0,9. Найти вероятность того, что взятое случайным образом изделие будет качественным.

Решение: Событие А – взятое изделие качественное.

Гипотезы: 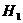- взятое изделие принадлежит 1 заводу,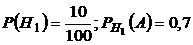

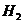- изделие принадлежит 2 заводу,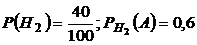

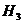- изделие принадлежит 3 заводу,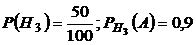

По формуле полной вероятности имеем

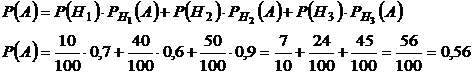
Ответ: 0,56.

Задание 4.

Дано распределение дискретной случайной величины Х. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение.

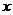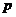	0,1	0,3	0,2	0,4

Решение:

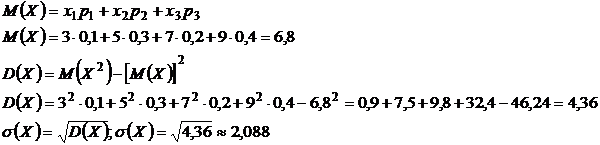
Ответ: .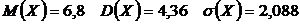

Задание 5.

В магазин поступают изделия с трех заводов: с 1 – 10%, со 2 -30%, с 3 – 60%. Среди изделий число первосортных составляет на 1 заводе 70%, на 2 – 90%, на 3 – 80%. Определить вероятность того, что купленное изделие выпущено третьим заводом.

Решение: Событие А – куплено первосортное изделие.

Гипотезы: 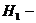изделие с 1 завода,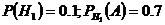

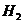- изделие со 2 завода,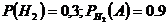

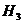- изделие со 3 завода,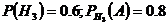

Тогда вероятность того, что купленное изделие выпущено третьим заводом найдем по формуле Байеса:

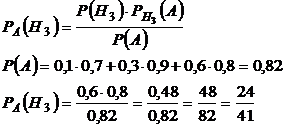
Ответ: .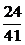

Задание 6.

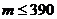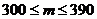Вероятность наступления события в каждом из 500 испытаний равна 0,7. Определить вероятность того, что число наступлений события удовлетворяет неравенству: а) б) в) .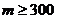

Решение. Воспользуемся формулой:

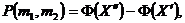где

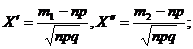
а)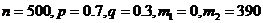

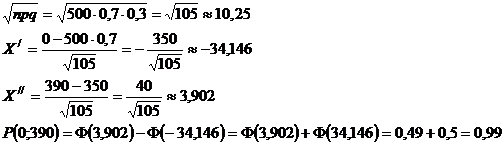
б)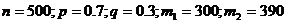

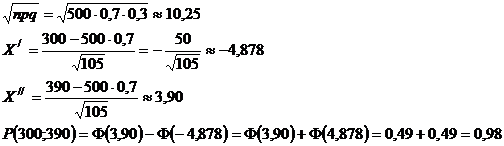
в)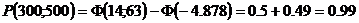

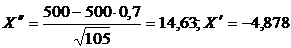
Ответ: а) 0,99; б) 0,98; в) 0,99.

Задание 7.

Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,002. Поступило 1000 вызовов. Определить вероятность 9 сбоев.

Решение: Число вызовов 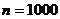велико, вероятность 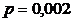мала. Воспользуемся формулой Пуассона

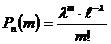, где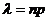

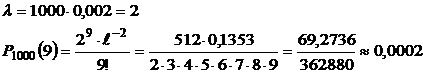
Ответ: 0,0002.

Задание 8.

Найти линейную среднюю квадратичную регрессию случайной величины Y на случайную величину X на основе закона распределения двумерной случайной величины.

y x
	0,1	0,24	0,3
	0,08	0,16	0,12

Решение: Уравнение линейной регрессии Y на X имеет вид

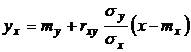
Найдем

Найдем вероятности значений

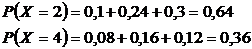
Определяем вероятность значений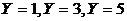

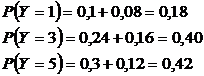
Находим

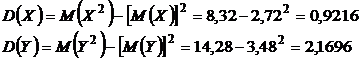
Следовательно,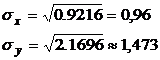

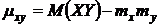, где

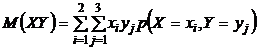
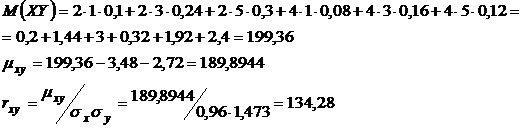
Подставляя полученные данные в уравнение 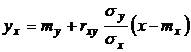имеем,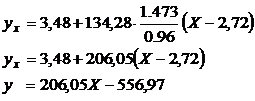

Ответ: .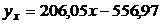

Задание 9.

Непрерывная случайная величина имеет нормальное распределение. Ее 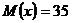, 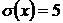. Найти вероятность того, что в результате испытания случайная величина примет значение в интервале (30;36).

Решение: Воспользуемся формулой

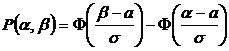, где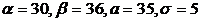

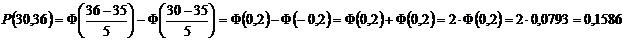Ответ: 0,1586.

Задание 10.

В двух партиях 70% и 50% доброкачественных изделий. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них:

а) хотя бы одно бракованное;

б) два бракованных;

в) одно доброкачественное и одно бракованное.

Решение: а)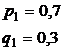

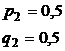
Событие А – хотя бы одно бракованное.

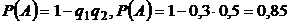
б) Событие В – два изделия бракованных:

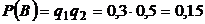
в) Событие С – 1 бракованное, 1 - доброкачественное.

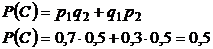
Ответ: а) 0,85; б) 0,15; в) 0,5.