Образец выполнения контрольной работы №7
Задание 1. Исследовать на сходимость, применяя признаки сравнения
а) 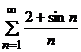
Решение: Так как 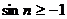 , то
, то 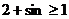 , откуда
, откуда 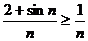 . Ряд
. Ряд 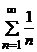 расходится, значит, расходится и больший ряд
расходится, значит, расходится и больший ряд 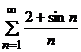 .
.
б) 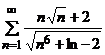
Решение: Учитывая, что и числитель, и знаменатель дроби 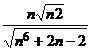
неограниченно растут при 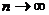 , запишем дробь, составленную из эквивалентных им выражений:
, запишем дробь, составленную из эквивалентных им выражений:
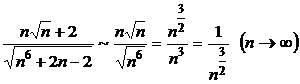 .
.
Так как ряд 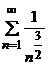 сходится, то сходится исходный ряд.
сходится, то сходится исходный ряд.
в) 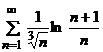
решение:
Так как 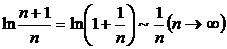 , то
, то 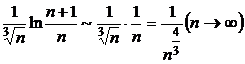 . Ряд
. Ряд 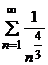 сходится, значит, сходится и исходный ряд.
сходится, значит, сходится и исходный ряд.
Задание 2. Исследовать на сходимость ряды, применяя, признак Коши (радикальный).
а) 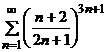 . б)
. б) 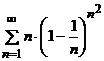 .
.
Решение:
а) Учитывая, что
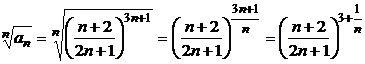 ,
,
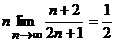 и
и 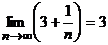 , получим
, получим
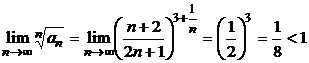 .
.
Исходный ряд сходится по признаку Коши.
б) Так как 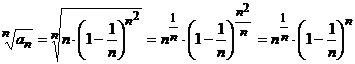 , то остается найти пределы
, то остается найти пределы 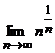 и
и 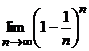 .
.
1) Поскольку 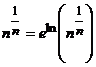 , где
, где 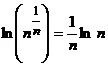 , то по правилу Лопиталя
, то по правилу Лопиталя 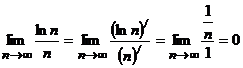 , откуда
, откуда 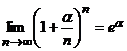 (следствие из 2-го замечательного предела), то
(следствие из 2-го замечательного предела), то 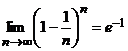 . Отсюда
. Отсюда
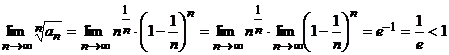 , и, значит, исходный ряд сходится.
, и, значит, исходный ряд сходится.
Задание 3. Исследовать на сходимость, применяя признак Даламбера.
а) 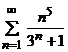 . б)
. б) 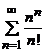 .
.
Решение: а) Преобразуем выражение 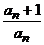 :
:
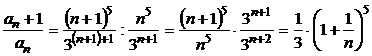 .
.
Так как 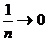 при
при 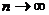 , то
, то 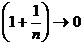 и
и 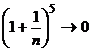 при
при 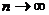 .
.
Значит, 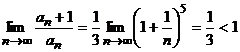 ,
,
И исходный ряд сходится по признаку Даламбера.
б) Поскольку
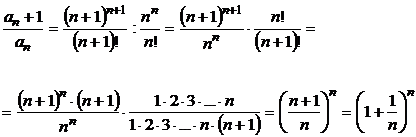
то 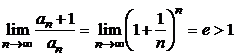 (2-й замечательный предел), и, значит, исходный ряд расходится.
(2-й замечательный предел), и, значит, исходный ряд расходится.
Задание 4.Исследовать на сходимость, применяя интегральный признак Коши. 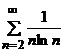
Решение: Так как 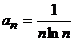 , то
, то 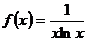 . Проверим применимость интегрального признака Коши. Очевидно, что функция
. Проверим применимость интегрального признака Коши. Очевидно, что функция 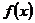 непрерывна и принимает только положительные значения на промежутке
непрерывна и принимает только положительные значения на промежутке 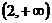 . Убедимся, что
. Убедимся, что 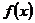 монотонно убывает на этом промежутке.
монотонно убывает на этом промежутке.
Пусть 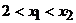 . Тогда
. Тогда 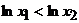 и
и 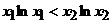 , откуда
, откуда 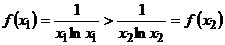 .
.
Итак, функция 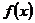 положительна, непрерывна и монотонно убывает на промежутке
положительна, непрерывна и монотонно убывает на промежутке 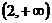 , значит, для использования данного ряда на сходимость можно применять интегральный признак сходимости.
, значит, для использования данного ряда на сходимость можно применять интегральный признак сходимости.
Найдем неопределенный интеграл 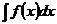 :
:
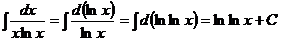 .
.
Первообразной для функции 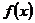 является, например, функция
является, например, функция 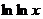 . Вычисляя несобственный интеграл
. Вычисляя несобственный интеграл 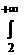 , получим
, получим
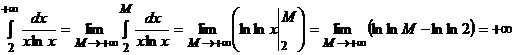 .
.
Так как несобственный интеграл 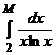 расходится, то расходится и ряд
расходится, то расходится и ряд 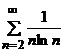 .
.
Задание 5.Исследовать на сходимость знакочередующиеся ряды.
а) 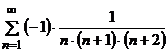 ; б)
; б) 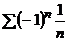 .
.
Решение:
а) 1) ряд из модулей: 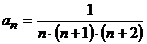 ;
;
2) исследуем ряд из модулей с помощью признака сравнения (предельного):
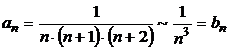 - сходящийся ряд.
- сходящийся ряд.
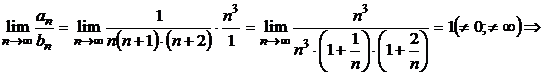
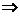 ряд
ряд 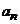 тоже сходится;
тоже сходится;
3) Исходный ряд сходится абсолютно.
б) 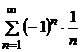
1) ряд из модулей: 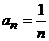 является расходящимся (гармонический ряд);
является расходящимся (гармонический ряд);
2) проверим условия признака Лейбница:
1. 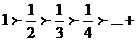 - выполняется;
- выполняется;
2. 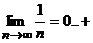 - выполняется.
- выполняется.
3) т.к. оба условия признака Лейбница выполнены, ряд исходный сходится условно.
Задание 6.определить радиус, интервал сходимости и выяснить поведение ряда на концах интервала сходимости.
а) 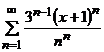 . б)
. б) 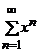 .
.
Решение:
а) Воспользуемся признаком Коши:
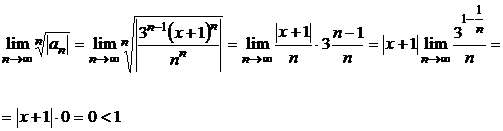
при всех 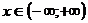 . Следовательно, ряд сходится в каждой точке числовой прямой
. Следовательно, ряд сходится в каждой точке числовой прямой 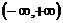 .
.
б) 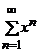 .
.
Применяем признак Даламбера:
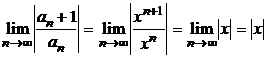 .
.
(Этот же результат можно получить, применяя признак Коши 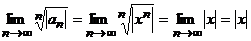 .) Отсюда следует, что при
.) Отсюда следует, что при 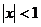 (т.е. при
(т.е. при 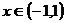 ) ряд сходится абсолютно, при
) ряд сходится абсолютно, при 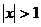 расходится. Таким образом, интервал
расходится. Таким образом, интервал 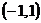 -интервал сходимости данного ряда. Исследуем ряд на сходимость в граничных точках этого интервала, т.е. в точках
-интервал сходимости данного ряда. Исследуем ряд на сходимость в граничных точках этого интервала, т.е. в точках 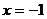 и
и 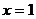
При 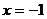 получим знакочередующийся ряд
получим знакочередующийся ряд
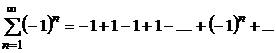
Этот ряд расходится, т.к. не выполнен необходимый признак сходимости 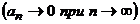 .
.
При 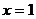 получим ряд
получим ряд 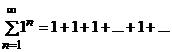
Этот ряд расходится по той же причине, так как
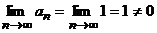
Итак, область сходимости данного ряда - интервал (-1,1).
Задание 7.
Разложить в ряд по степеням 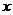 функцию
функцию 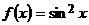 .
.
Решение
Продифференцируем функцию 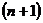 раз:
раз: 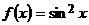 .
.
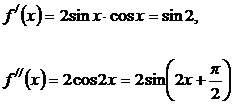
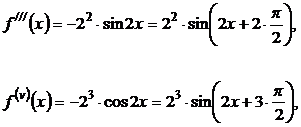
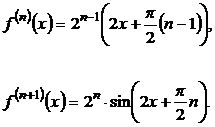
Находим значения функций: 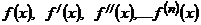 в точке
в точке 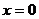 , а значение
, а значение 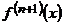 определяем в точке
определяем в точке 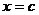 (см. остаточный член в форме Лагранжа). Получаем:
(см. остаточный член в форме Лагранжа). Получаем: 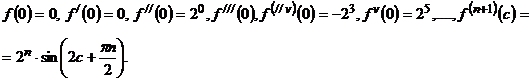
Находим остаточный член:
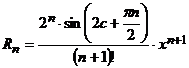 , т.е.
, т.е. 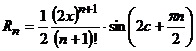 .
.
Так как 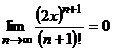 при любом
при любом 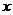 , а
, а 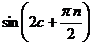 - величина ограниченная, то
- величина ограниченная, то 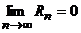 . Следовательно, функцию
. Следовательно, функцию 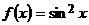 можно представить в виде суммы ряда Маклорена
можно представить в виде суммы ряда Маклорена 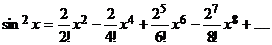
Задание 8.Проинтегрировать, применяя разложение в ряд. 
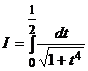 с точностью до 0,0001
с точностью до 0,0001
Решение: Разложим подынтегральную функцию в биномиальный ряд, полагая в нем 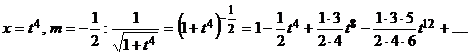
Этот ряд сходится к биному 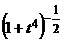 при
при 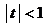 . Интегрируя в пределах от 0 до
. Интегрируя в пределах от 0 до 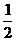 , найдем
, найдем 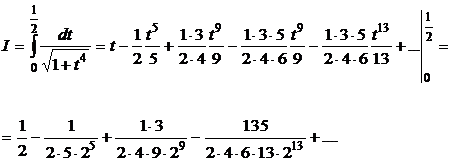
Вычислим несколько последовательных первых членов полученного знакочередующегося сходящего ряда (с одним лишним знаком): 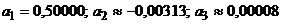 .
.
Согласно свойству знакочередующегося сходящегося ряда, для вычисления интеграла с точностью до 0,0001 достаточно взять сумму двух первых членов ряда 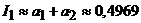 .
.
Ошибка этого приближенного значения меньше абсолютного значения первого из отброшенных членов ряда, т.е. меньше 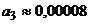 .
.
Задание 9.Решить уравнение с помощью степного ряда.
Пример 1. Найти решение уравнения 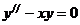 ,
,
если 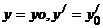 при
при 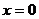 .
.
Решение. Полагаем 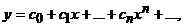
Отсюда, дифференцируя, получим:
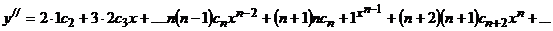
Подставляя 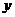 и
и 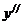 в данное уравнение, приходим к тождеству
в данное уравнение, приходим к тождеству
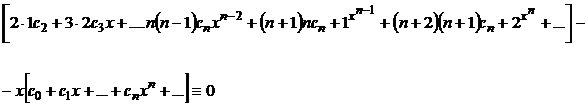
Собирая в левой части полученного равенства члены с одинаковыми степенями 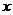 и приравнивая нулю коэффициенты при этих степенях, будем иметь
и приравнивая нулю коэффициенты при этих степенях, будем иметь
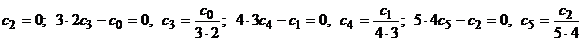 и т.д.
и т.д.
Вообще,
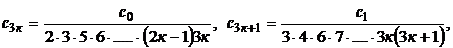
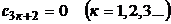 .
.
Следовательно,
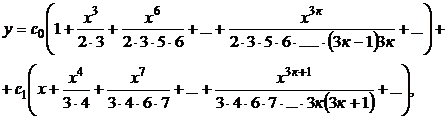
где 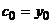 и
и 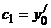 .
.
Задание 2. Найти решения уравнения 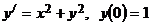 .
.
Решение: Из уравнения начальных условий находим 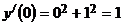 . Дифференцируя данное уравнение, последовательно получаем
. Дифференцируя данное уравнение, последовательно получаем
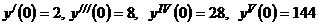 . Искомое решение имеет вид
. Искомое решение имеет вид
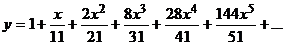 .
.
Задание 10. Вычислить с точностью до 0,001: а) 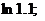 б)
б) 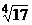 .
.
Решение: а) Возьмем ряд для функции 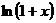 .
.
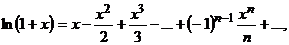
который сходится к 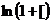 в интервале
в интервале 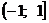 , и, полагая
, и, полагая 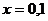 , получим ряд для вычисления
, получим ряд для вычисления 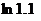 с любой точностью:
с любой точностью:
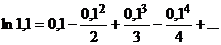
Абсолютное значение четвертого члена этого ряда меньше 0,0001. Поэтому, согласно свойству знакочередующегося сходящегося ряда, для вычисления приближенного значения 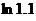 с точностью до 0,0001 достаточно взять сумму трех первых членов ряда
с точностью до 0,0001 достаточно взять сумму трех первых членов ряда
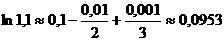 .
.
б) Преобразуем, данный корень 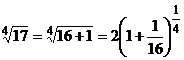 и принимаем биномиальный ряд, полагая
и принимаем биномиальный ряд, полагая 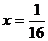 ,
, 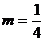 .
.
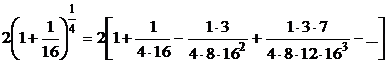 .
.
Чтобы определить, сколько взять первых членов этого знакочередующегося сходящегося ряда для вычисления 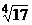 с точностью до 0,0001, вычисляем несколько последовательных первых членов ряда:
с точностью до 0,0001, вычисляем несколько последовательных первых членов ряда: 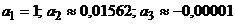 .
.
Согласно свойству знакочередующегося сходящегося ряда, если ограничиться суммой трех первых членов ряда, то ошибка искомого приближенного значения корня будет меньше 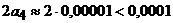 . Следовательно,
. Следовательно, 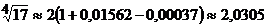 .
.
Задание 11. Вычислить двойной интеграл 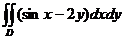 по области, ограниченной линиями
по области, ограниченной линиями
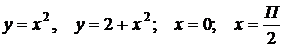 .
.
Решение: Указанная область ограничена правыми ветвями парабол 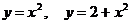 и вертикальными прямыми
и вертикальными прямыми 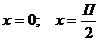 . Так как область D является правильной в направлении оси ОY, приведем двойной интеграл к повторному по формуле
. Так как область D является правильной в направлении оси ОY, приведем двойной интеграл к повторному по формуле
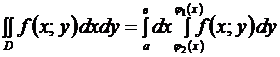 ( внешнее интегрирование ведется по переменной х, а внутреннее – по y).
( внешнее интегрирование ведется по переменной х, а внутреннее – по y).
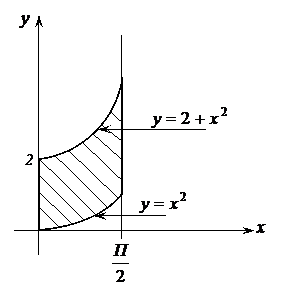 |
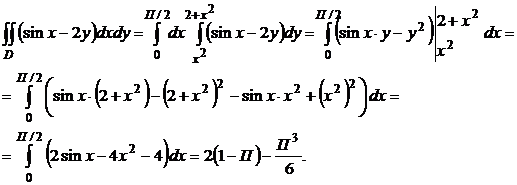
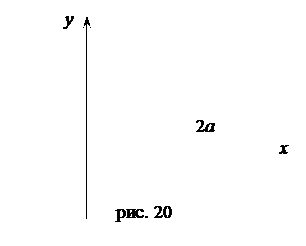
Задание 12. Вычислить двойной интеграл, используя переход к полярным координатам 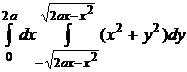 .
.
Решение. Область интегрирования D ограничена полуокружностями 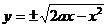 одной окружности,
одной окружности, 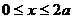 .
.
Преобразуем уравнения границ к полярным координатам .Подставим формулы перехода 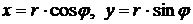 в уравнение окружности. Так как
в уравнение окружности. Так как 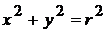 , то уравнение окружности
, то уравнение окружности 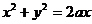 преобразуется к виду
преобразуется к виду 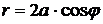 . Поэтому областью D* является область, снизу ограниченная осью
. Поэтому областью D* является область, снизу ограниченная осью 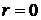 , сверху косинусоидой
, сверху косинусоидой 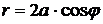 , причем
, причем 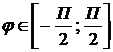 .
.












|

Задание 13. Вычислить площадь плоской области, ограниченной линиями 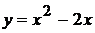 ;
; 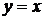 .
.
Решение:Построим данную фигуру (рис. 25).
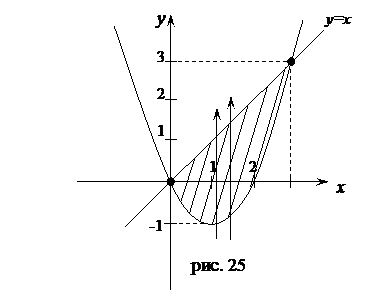
Найдем аналитически т. пересечения линий:
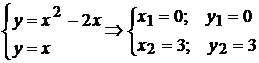 .
.
В области D справедливы неравенства: 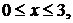
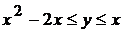 .
.
Искомая площадь: 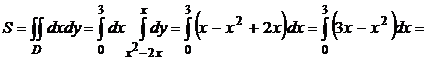
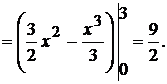
Задание 14.
Вычислить объём тела, ограниченного цилиндрической поверхностью 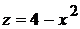 , плоскостями
, плоскостями 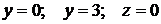 .
.
Решение: Данное тело ограничено координатными плоскостями 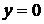 (ХОZ),
(ХОZ), 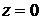 (ХОУ), плоскостью
(ХОУ), плоскостью 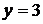 , параллельной плоскости ХОZ, проходящей через т.
, параллельной плоскости ХОZ, проходящей через т. 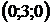 и параболическим цилиндром
и параболическим цилиндром 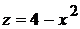 . Построим данное тело и его проекцию.
. Построим данное тело и его проекцию.
Искомый объем 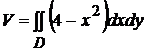 .
.
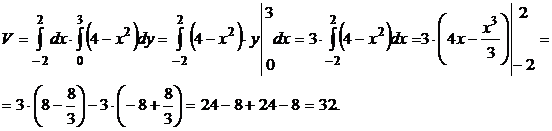
Задание 15. Вычислить массу материальной пластинки, принадлежащей плоскости Оху, и ограниченной линиями 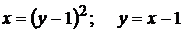 , если её поверхностная плотность
, если её поверхностная плотность 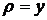 .
.
Решение.
Напомним, что из физического смысла интеграла следует, что масса m материальной пластинки D вычисляется по формуле:
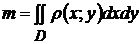 ,
,
где 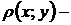 плотность, с которой распределена масса.
плотность, с которой распределена масса.
Построим линии, ограничивающие пластинку:
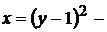 кв. парабола с осью симметрии
кв. парабола с осью симметрии 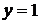 ;
;
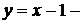 прямая, походящая через т. (0; -1); (1;0)
прямая, походящая через т. (0; -1); (1;0)
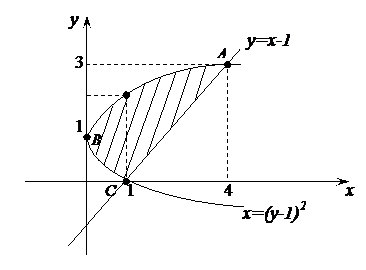

Точка пересечения линий: 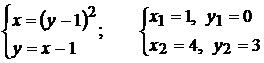
Пластинка АВС – правильная область в направлении оси Ох,
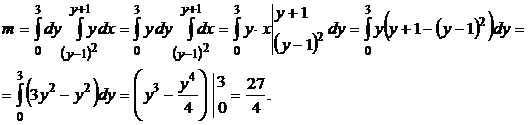
Задание 16. Расставить пределы интегрирования в тройном интеграле 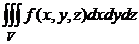 , если область интегрирования V ограничена поверхностями
, если область интегрирования V ограничена поверхностями 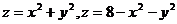 .
.
Решение.Указанная область V ограничена снизу восходящим параболоидом вращения 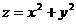 с вершиной в точке (0,0,0), сверху - нисходящим параболоидом вращения
с вершиной в точке (0,0,0), сверху - нисходящим параболоидом вращения 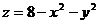 с вершиной (0,0,8) (рис.2.3.).
с вершиной (0,0,8) (рис.2.3.).
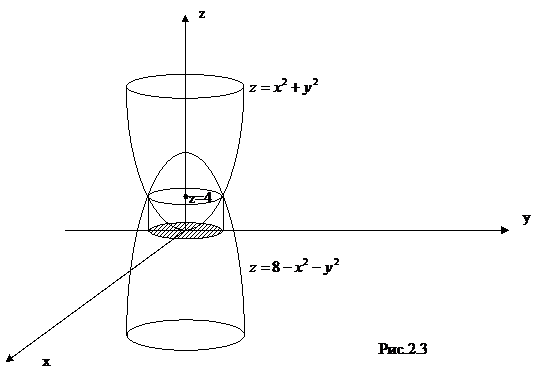
Найдем линию пересечения поверхностей, исключив переменную z из уравнений параболоидов: 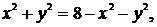
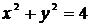 .
.
Имеем окружность 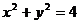 в плоскости z=4. Таким образом, проекция области V на плоскость Oxy есть окружность
в плоскости z=4. Таким образом, проекция области V на плоскость Oxy есть окружность 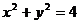 , для точек которой верны неравенства
, для точек которой верны неравенства 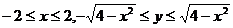 .
.
Значит,
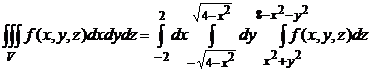 .
.
Задание 17. Вычислить координаты центра масс однородного тела, занимающего область V, ограниченную поверхностями 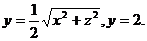
Решение. Тело представляет полуконус 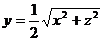 с осью симметрии OY, ограниченный плоскостью y=2.
с осью симметрии OY, ограниченный плоскостью y=2.
Ввиду симметрии тела относительно OY координаты 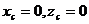 , а
, а
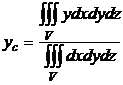 .
.
Перейдем к цилиндрическим координатам по формулам 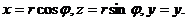 Тогда
Тогда
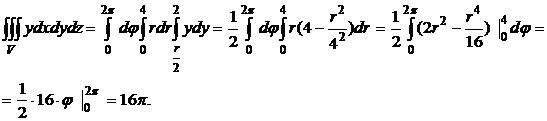
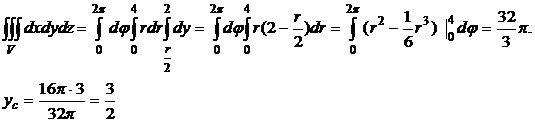
Значит центр масс С ( 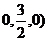 .
.
Задание 18.
Вычислить момент инерции относительно оси ОY однородного тела V, ограниченного поверхностью 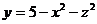 и плоскостью y=1, плотность
и плоскостью y=1, плотность 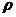
принять равной 1.
Решение. Моменты инерции 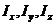 относительно координатных осей вычисляются согласно формулам
относительно координатных осей вычисляются согласно формулам 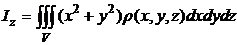
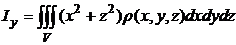
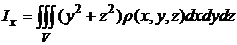 , здесь
, здесь 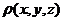 - объемная плотность .
- объемная плотность .
Тело V ограничено параболоидом вращения 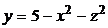 с осью симметрии ОY, отсеченным плоскостью y=1.
с осью симметрии ОY, отсеченным плоскостью y=1.
Тогда искомый момент
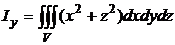 .
.
Перейдем к цилиндрическим координатам по формулам
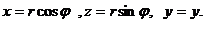
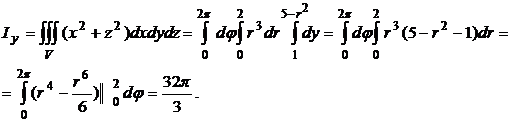
Контрольная работа №8
