Образец выполнения контрольной работы №5.
I. Вычислить неопределенный интеграл.
а) 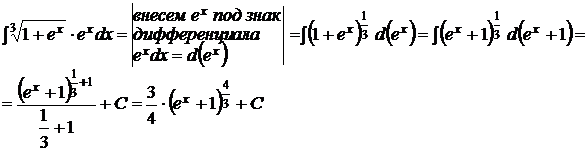
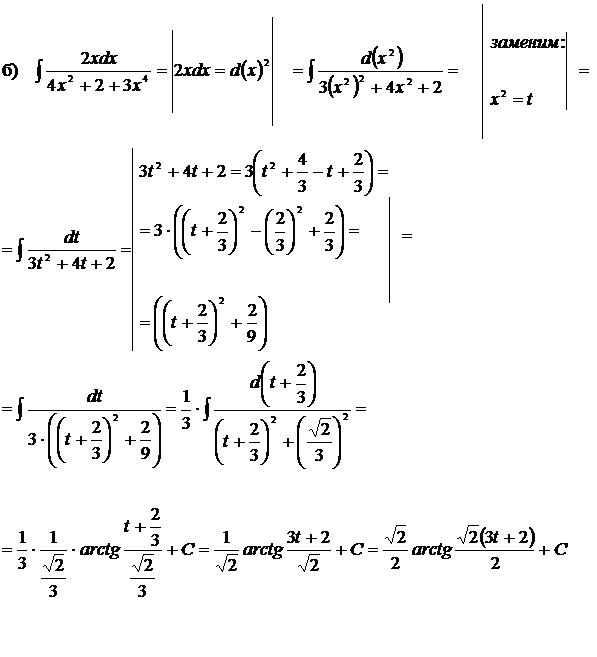
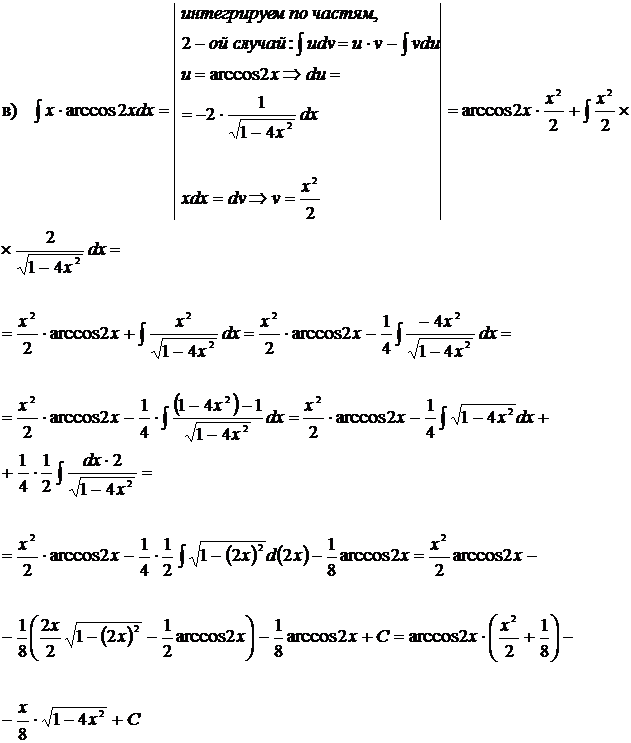
г) 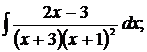
1) Разложим подынтегральную функцию на простейшие дроби:
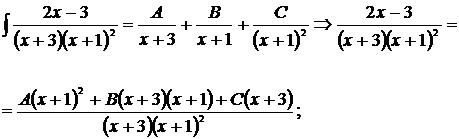
2) Прировняем числители:
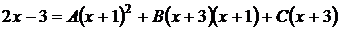
3) Найдем неизвестные коэффициенты А, В и С, комбинируя два метода:
метод частных значений (МЧЗ) и метод приравнивания коэффициентов (МПК).
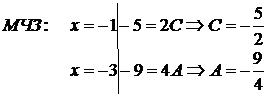
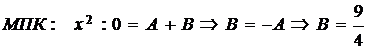
4) Таким образом, 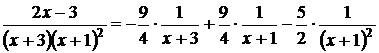
5)
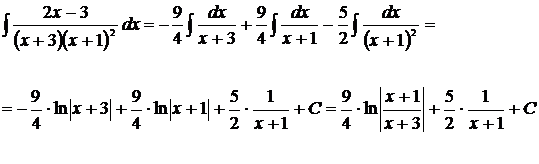
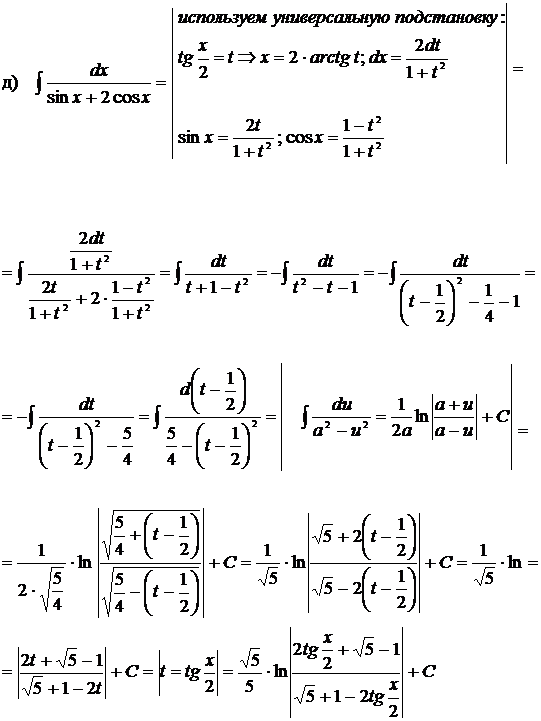

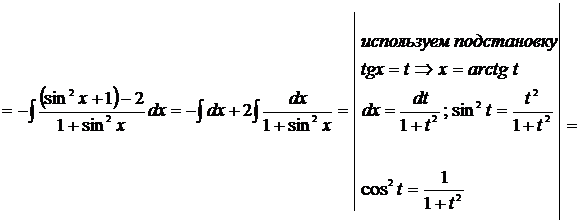
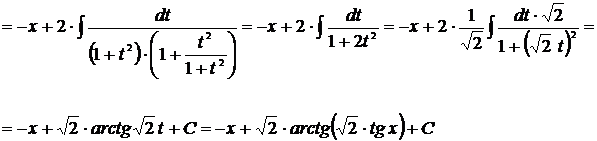
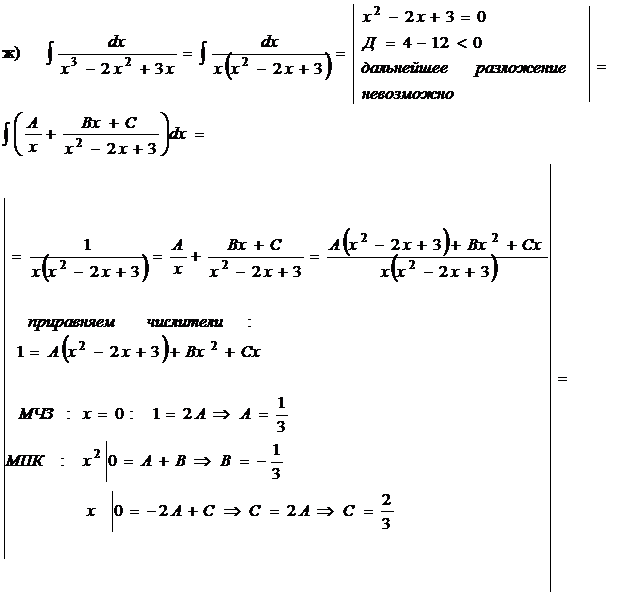
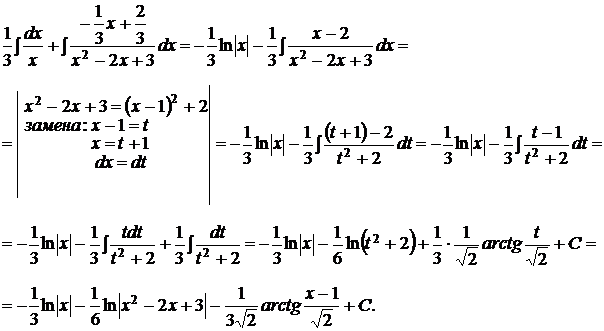
II. Вычислить определенный интеграл:
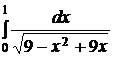
Решение: а) Выделим полный квадрат в выражении
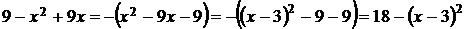
б) Сделаем замену: 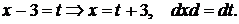
Пределы интегрирования также изменяется: 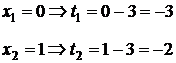
в) 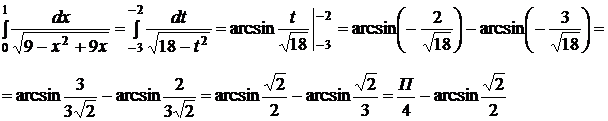
Ответ 
III. найти длину кардиоиды 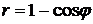
Решение:
а) Формула для вычисления длины дуги, заданной в полярной системе координат:
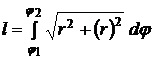
б) Для кардиоиды 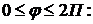
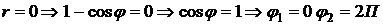
в) 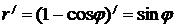
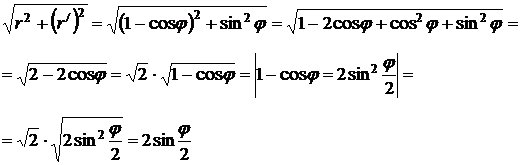
г) Так как кардиоиды симметрична относительно полярной оси, можно найти половину дуги, затем это значение удвоить; при этом 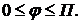
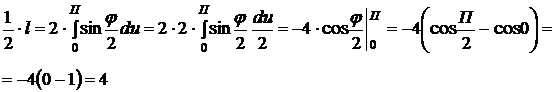
Значит, 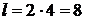
Ответ: 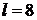
IV. Показать расходимость или вычислить несобственный интеграл:
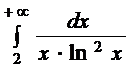
Решение:
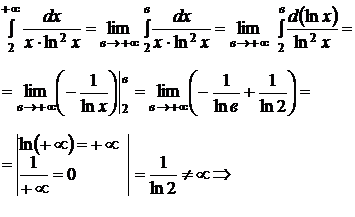
несобственный интеграл сходиться и его значение равно 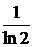
 Контрольная работа №6
Контрольная работа №6
Обыкновенные дифференциальные уравнения и системы.
1. Определить вид дифференциальных уравнений и проинтегрировать их.
2. Найти общий интеграл дифференциального уравнения.
3. Определить вид дифференциальных уравнений и проинтегрировать их.
4. Определить вид дифференциальных уравнений и проинтегрировать их.
5. Определить вид дифференциальных уравнений и проинтегрировать их.
6. Определить вид дифференциальных уравнений и проинтегрировать их.
7. Решить дифференциальное уравнения второго порядка с постоянными коэффициентами методом неопределенных коэффициентов.
8. Решить однородное дифференциальное уравнение высших порядков.
9. Решить дифференциальное уравнение методом вариации произвольных постоянных (Лагранжа), удовлетворяющих начальным условиям.
10. Решить систему дифференциальных уравнений при начальных условиях
11. Составить и решить дифференциальное уравнение
Вариант 1
1. 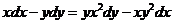
2. 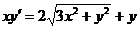
3. 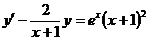
4. 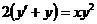
5. 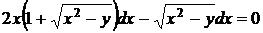
6. 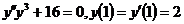
7. 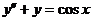
8. 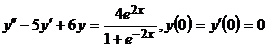
9. 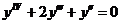
10. 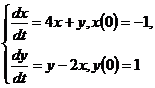
11. Материальная точка массой m = 2 г погружается в жидкость, сила сопротивления которой пропорциональна скорости погружения с коэффициентом пропорциональности k = 0,002 кг/с. Найти скорость точки через 1 с после начала погружения, если в начальный момент она была равна нулю.
Вариант 2
1. 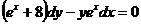
2. 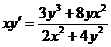
3. 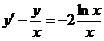
4. 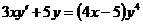
5. 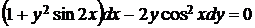
6. 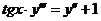
7. 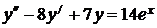
8. 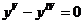
9. 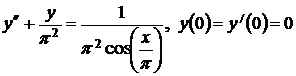
10. 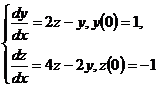
11. Моторная лодка двигалась в спокойной воде со скоростью υ0 = 10 км/ч. На полном ходу ее мотор был выключен и через 20 с скорость лодки уменьшилась до υl = 6 км/ч. Сила сопротивления воды пропорциональна скорости движения лодки. Найти скорость лодки, а также расстояние, пройденное лодкой через 2 мин после остановки мотора.
Вариант 3
1. 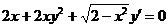
2. 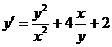
3. 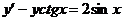
4. 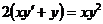
5. 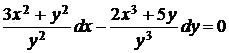
6. 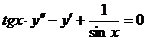
7. 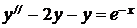
8. 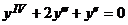
9. 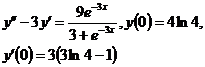
10. 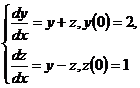
11. Пуля, двигаясь со скоростью υ0 = 400 м/с, ударяется о достаточно толстую стену и начинает углубляться в нее, испытывая силу сопротивления стены; эта сила сообщает пуле отрицательное ускорение, пропорциональное квадрату ее скорости с коэффициентом пропорциональности k = 7 м-1. Найти скорость пули через 0,001 с после вхождения пули в стену.
Вариант 4
1. 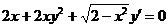
2. 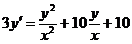
3. 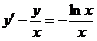
4. 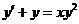
5. 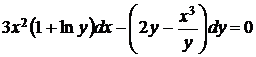
6. 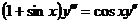
7. 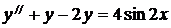
8. 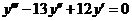
9. 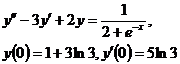
10. 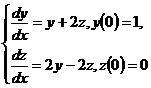
11. Материальная точка массой m = 1 г движется прямолинейно. На нее действует сила в направлении движения, пропорциональная времени с коэффициентом пропорциональности k1=2·10-5 кг·м/с3, и сила сопротивления среды, пропорциональная скорости с коэффициентом пропорциональности k2=0,003 кг/с. Найти скорость точки через 3 с после начала движения, если начальная скорость точки была равна нулю.
Вариант 5
1. 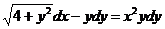
2. 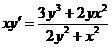
3. 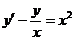
4. 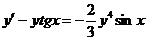
5. 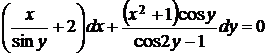
6. 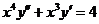
7. 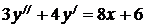
8. 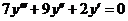
9. 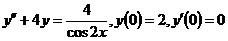
10. 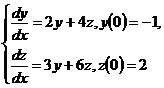
11. В сосуде 100 л водного раствора соли. В сосуд втекает чистая вода со скоростью q =5 л/мин, а смесь вытекает с той же скоростью, причем перемешивание обеспечивает равномерную концентрацию раствора. В начальный момент в растворе содержалось m0 = 10 кг соли. Сколько соли будет содержаться в сосуде через 20 мин после начала процесса?
Вариант 6
1. 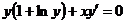
2. 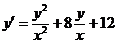
3. 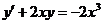
4. 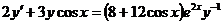
5. 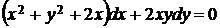
6. 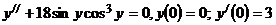
7. 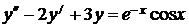
8. 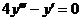
9. 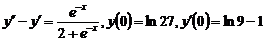
10. 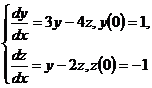
11. Кривая проходит через точку А(2;-1) и обладает тем свойством, что угловой коэффициент касательной в любой ее точке пропорционален квадрату ординаты точки касания с коэффициентом пропорциональности k=3. Найти уравнение кривой.
Вариант 7
1. 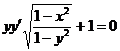
2. 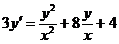
3. 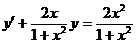
4. 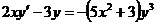
5. 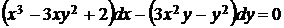
6. 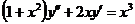
7. 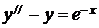
8. 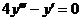
9. 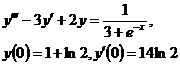
10. 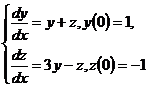
11. Кривая проходит через точку А(1;2) и обладает тем свойством, что произведение углового коэффициента касательной в любой ее точке на сумму координат точки касания равно удвоенной ординате этой точки. Найти уравнение кривой.
Вариант 8
1. 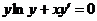
2. 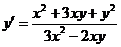
3. 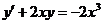
4. 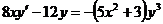
5. 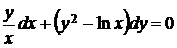
6. 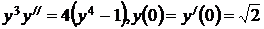
7. 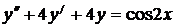
8. 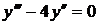
9. 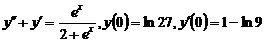
10. 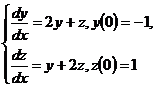
11. Кривая проходит через точку А(1;2) и обладает тем свойством, что отношение ординаты любой ее точки к абсциссе пропорционально угловому коэффициенту касательной к этой кривой, проведенной в той же точке, с коэффициентом пропорциональности k = 3. Найти уравнение кривой.
Вариант 9
1. 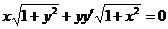
2. 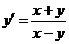
3. 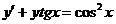
4. 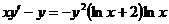
5. 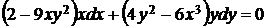
6. 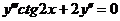
7. 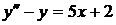
8. 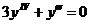
9. 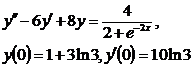
10. 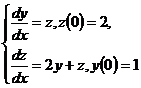
11. Кривая проходит через точку А(1;5) и обладает тем свойством, что отрезок, отсекаемый на оси ординат любой касательной, равен утроенной абсциссе точки касании. Найти уравнение кривой.
Вариант 10
1. 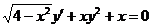
2. 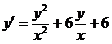
3. 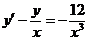
4. 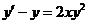
5. 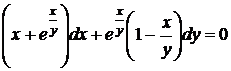
6. 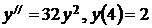
7. 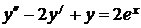
8. 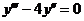
9. 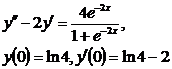
10. 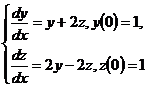
11. Кривая проходит через точку А(2;4) и обладает тем свойством, что отрезок, отсекаемый на оси абсцисс касательной, проведенной в любой точке кривой, равен кубу абсциссы точки касания. Найти уравнение кривой.
Вариант 11
1. 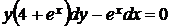
2. 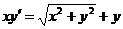
3. 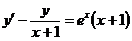
4. 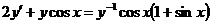
5. 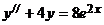
6. 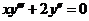
7. 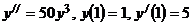
8. 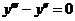
9. 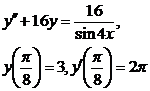
10. 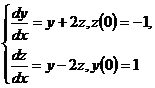
11. Найти кривую, проходящую через точку А(1;0) и такую, что отрезок, отсекаемый касательной на оси ординат, равен абсциссе точки касания.
Вариант 12
1. 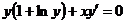
2. 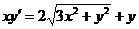
3. 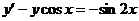
4. 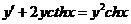
5. 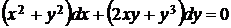
6. 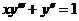
7. 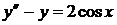
8. 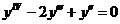
9. 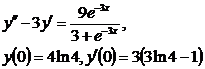
10. 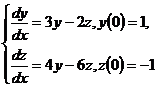
11. Найти уравнение кривой, проходящей через точу А(1;1), у которой подкасательная равна сумме координат точки касания.
Вариант 13
1. 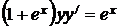
2. 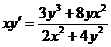
3. 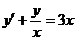
4. 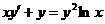
5. 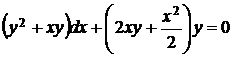
6. 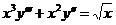
7. 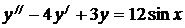
8. 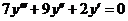
9. 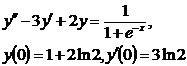
10. 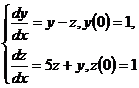
11. Найти кривую, проходящую через точку А(2;16), зная, что угловой коэффициент касательной в любой точке кривой: в 3 раза больше углового коэффициента прямой, соединяющей эту же точку с началом координат.
Вариант 14
1. 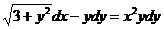
2. 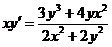
3. 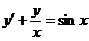
4. 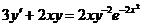
5. 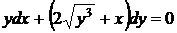
6. 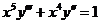
7. 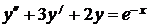
8. 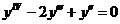
9. 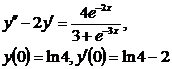
10. 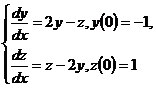
11. Найти кривую, проходящую через точку А(2;16), зная, что угловой коэффициент касательной в любой точке кривой: равен квадрату ординаты этой точки.
Вариант 15
1. 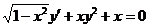
2. 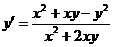
3. 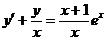
4. 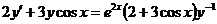
5. 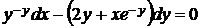
6. 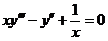
7. 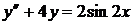
8. 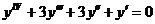
9. 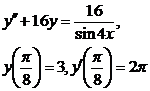
10. 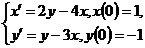
11. Найти уравнение кривой, проходящей через точку А(4;1), для которой: отрезок любой касательной к кривой, заключенный между осями координат, делится точкой касания пополам.
Вариант 16
1. 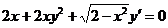
2. 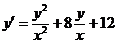
3. 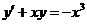
4. 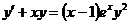
5. 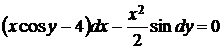
6. 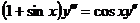
7. 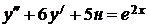
8. 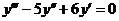
9. 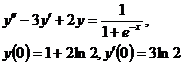
10. 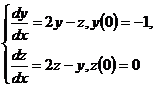
11. Найти уравнение кривой, проходящей через точку А(4;1), для которой: отрезок касательной между точкой касания и осью абсцисс делится пополам в точке пересечения с осью ординат.
Вариант 17
1. 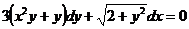
2. 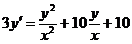
3. 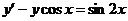
4. 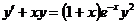
5. 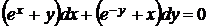
6. 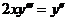
7. 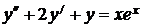
8. 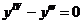
9. 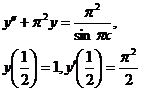
10. 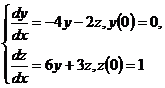
11. Найти кривую, проходящую через точку А(1;1), для которой площадь треугольника, образованного касательной, ординатой точки касания и осью абсцисс, равна 1.
Вариант 18
1. 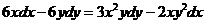
2. 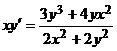
3. 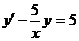
4. 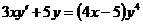
5. 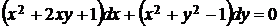
6. 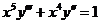
7. 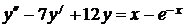
8. 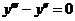
9. 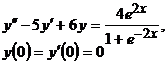
10. 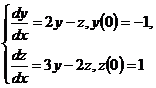
11. Найти кривую, у которой сумма длин касательной (точнее длины ее отрезка от точки касания до точки пересечения с осью абсцисс) и подкасательной в любой ее точке равна произведению координат точки касания.
Вариант 19
1. 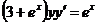
2. 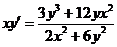
3. 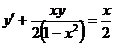
4. 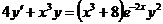
5. 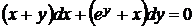
6. 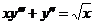
7. 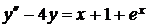
8. 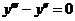
9. 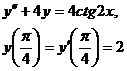
10. 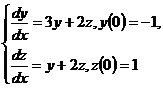
11. Известно, что тело охлаждается в течение 15 мин от 1000 С до 800 С. Через сколько минут температура тела понизится до 400 С, если температура окружающей среды 100 С (скорость охлаждения тела пропорциональна разности температур тела и окружающей среды).
Вариант 20
1. 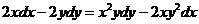
2. 
3. 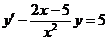
4. 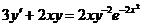
5. 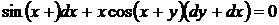
6. 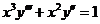
7. 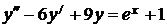
8. 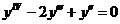
9. 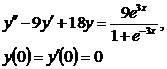
10. 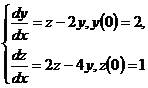
11. Определить численность населения России через 20 лет, считая что скорость прироста населения пропорциональна его начальному количеству, и зная, что население России в 2000 году составляла 145 млн. человек, а прирост населения за 2000 год был равен α = 2 %.
Вариант 21
1. 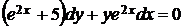
2. 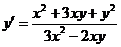
3. 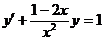
4. 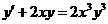
5. 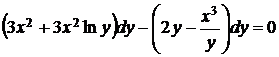
6. 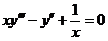
7. 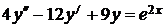
8. 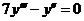
9. 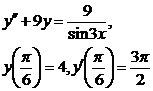
10. 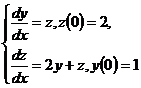
11. Вращающийся в жидкости диск замедляет свое движение под действием силы трения, пропорциональной угловой скорости вращения ω. Известно, что диск, начавший вращаться со скоростью 18 об/с, по истечении 45 с вращается со скоростью 6 об/с. С какой угловой скоростью будет вращаться диск по истечении 90 с после начала замедления? В какой момент времени ω будет равняться 1 об/с?
Вариант 22
1. 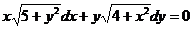
2. 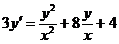
3. 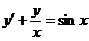
4. 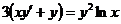
5. 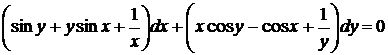
6. 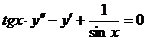
7. 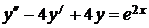
8. 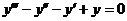
9. 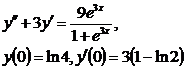
10. 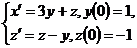
11. Найти кривую, проходящую через точку А(3;0), если известно, что угловой коэффициент касательной равен (х + у)/х.
Вариант 23
1. 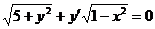
2. 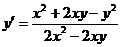
3. 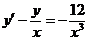
4. 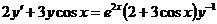
5. 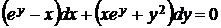
6. 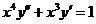
7. 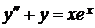
8. 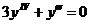
9. 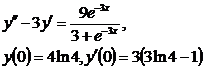
10. 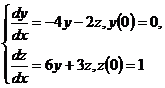
11. Найти кривую, проходящую через точку А(1;0), если известно, что треугольник, образованный осью ординат, касательной к кривой в произвольной ее точке и радиус-вектором точки касания, равнобедренный; основанием его является отрезок касательной от точки касания до оси ординат.
Вариант 24
1. 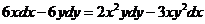
2. 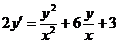
3. 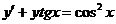
4. 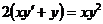
5. 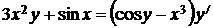
6. 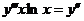
7. 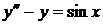
8. 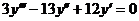
9. 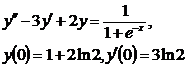
10. 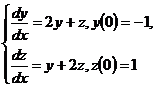
11. Скорость распада радия пропорциональна количеству нераспавшегося радия. Количество радия в начале процесса (t = 0) было равно N0. Известно, что за 1600 лет распадается половина первоначального количества. Через сколько лет количество нераспавшегося радия будет составлять 80 % первоначального? Определить какой процент радия сохраниться через 300 лет?
Вариант 25
1. 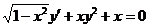
2. 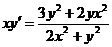
3. 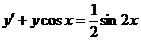
4. 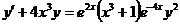
5. 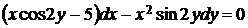
6. 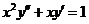
7. 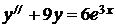
8. 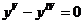
9. 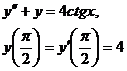
10. 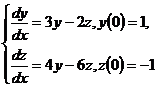
11. Скорость охлаждения нагретого тела пропорциональна разности температур тела и окружающей среды. Температура среды постоянна и равна Tср = 200 С. Определить, за какое время тело, нагретое до температуры T0=3000 C, охладится до 1500 С. При этом известно, что через 10 мин после начала процесса охлаждения температура тела равна 2000 С.
Вариант 26
1. 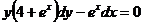
2. 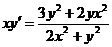
3. 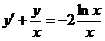
4. 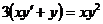
5. 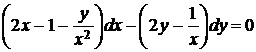
6. 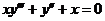
7. 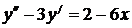
8. 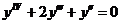
9. 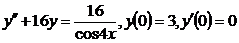
10. 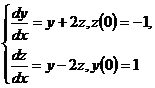
11. Тело, двигаясь горизонтально, замедляет свое движение под действием силы сопротивления среды, пропорциональной квадрату скорости. Найти зависимость скорости от времени, если υ(0) = 20 м/с, а υ(1) = 10 м/с. Найти скорость точки через три секунды после начала торможения и расстояние, пройденное ею за это же время.
Вариант 27
1. 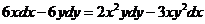
2. 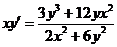
3. 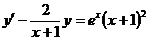
4. 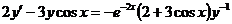
5. 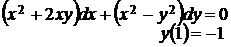
6. 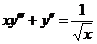
7. 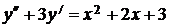
8. 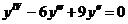
9. 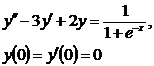
10. 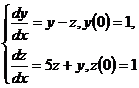
11. Материальная точка массой m погружается с ненулевой начальной скоростью в жидкость. На нее действует сила тяжести и сила сопротивления жидкости, пропорциональная скорости погружения. Найти зависимость скорости движения точки от времени.
Вариант 28
1. 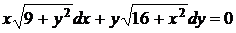
2. 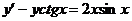
3. 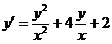
4. 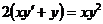
5. 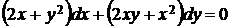
6. 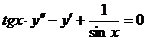
7. 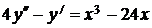
8. 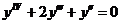
9. 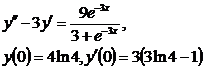
10. 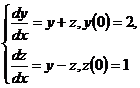
11. Найти кривые, у которых площадь треугольника, образованного осью абсцисс, касательной и радиусом-вектором точки касания, постоянна и равна 4.
Вариант 29
1. 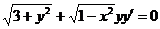
2. 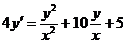
3. 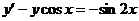
4. 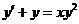
5. 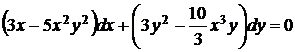
6. 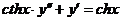
7. 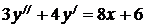
8. 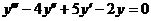
9. 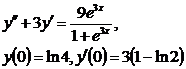
10. 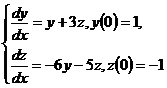
11. Найти кривую, проходящую через точку А(1;2), касательная которой в произвольной ее точке отсекает на оси ординат отрезок, равный квадрату ординаты точки касания.
Вариант 30
1. 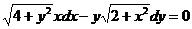
2. 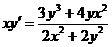
3. 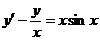
4. 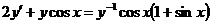
5. 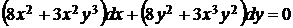
6. 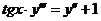
7. 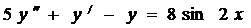
8. 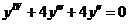
9. 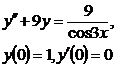
10. 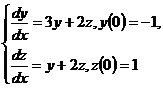
11. Найти семейство кривых, подкасательная в любой точке которых равна среднему арифметическому координат точки касания.
