Образец выполнения контрольной работы №3.
Задание 1. Найти пределы, не применяя правило Лопиталя.
1. 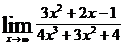
2. 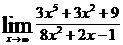
3. 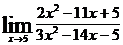
4. 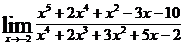
5. 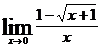
6. а) 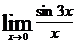 ; б)
; б) 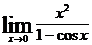
7. 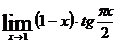
8. 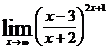
Решение:
1. Здесь х→∞, при этом числитель и знаменатель также стремятся к ∞. Символически этот случай обозначают 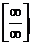 и называют «неопределенностью типа
и называют «неопределенностью типа 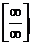 ». Очевидно, что непосредственно применить теорему о пределе частного здесь нельзя. Преобразуем предварительно данную дробь, разделив и числитель, и знаменатель на х3 (старшая степень знаменателя).
». Очевидно, что непосредственно применить теорему о пределе частного здесь нельзя. Преобразуем предварительно данную дробь, разделив и числитель, и знаменатель на х3 (старшая степень знаменателя).
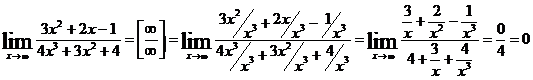 .
.
(Величины 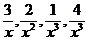 - бесконечно малые, при х→∞ их пределы равны нулю).
- бесконечно малые, при х→∞ их пределы равны нулю).
2. Имеем неопределенность типа 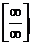 . Старшая степень числителя равна 5, а старшая степень знаменателя 2. Числитель, и знаменатель поделим на х5.
. Старшая степень числителя равна 5, а старшая степень знаменателя 2. Числитель, и знаменатель поделим на х5.
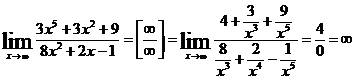 .
.
Предел числителя в полученной дроби равен 4, а предел знаменателя равен нулю, знаменатель при х→∞ - величина бесконечно малая (теорему о пределе частного применить нельзя). Итак, наша дробь, как величина, обратная бесконечно малой, является бесконечно большой величиной и ее предел равен бесконечности.
3. Разложим числитель и знаменатель дроби на множители, по формуле: 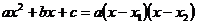 , где х1 и х2 – корни квадратного трехчлена. Затем сократим дробь на (х-5).
, где х1 и х2 – корни квадратного трехчлена. Затем сократим дробь на (х-5).
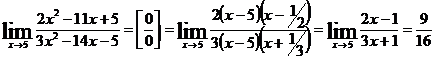 .
.
4. Сократим дробь, разделив на (х+2) числитель и знаменатель в отдельности.
_ 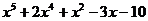 | 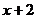 | _ 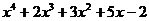 | 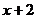 | |
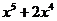 | 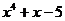 | 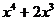 | 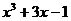 | |
_ 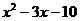 | _ 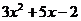 | |||
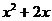 | и | 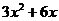 | ||
_ 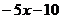 | _ 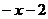 | |||
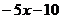 | 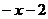 | |||
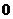 | 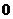 |
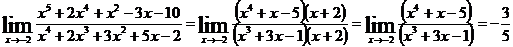 .
.
Вообще, если ищется предел дроби, при 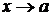 числитель и знаменатель которой многочлены, обращающиеся в нуль в предельной точке х = а, то согласно теореме Безу оба многочлена разделятся без остатка на (х – а), т.е. такую дробь всегда можно сократить на ( х – а).
числитель и знаменатель которой многочлены, обращающиеся в нуль в предельной точке х = а, то согласно теореме Безу оба многочлена разделятся без остатка на (х – а), т.е. такую дробь всегда можно сократить на ( х – а).
5. Выяснив вначале, что при указанном изменении аргумента данная функция представляет отношение двух бесконечно малых величин (случай 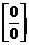 ), преобразуем затем дробь так, чтобы сократить ее на множитель, стремящийся к нулю: переведем иррациональность из числителя в знаменатель путем умножения числителя и знаменателя на
), преобразуем затем дробь так, чтобы сократить ее на множитель, стремящийся к нулю: переведем иррациональность из числителя в знаменатель путем умножения числителя и знаменателя на 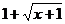 , затем сократим дробь на х:
, затем сократим дробь на х:
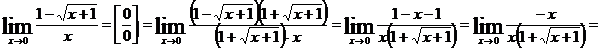
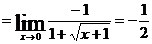 .
.
6. Устанавливаем, что данная функция не определена в предельной точке, и при заданном изменении аргумента она представляет отношение двух бесконечно малых величин (случай  ). После этого подвергаем функцию преобразованиям, чтобы использовать 1-й замечательный предел:
). После этого подвергаем функцию преобразованиям, чтобы использовать 1-й замечательный предел: 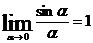 (α – радианная мера угла).
(α – радианная мера угла).
а) 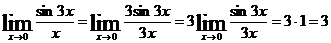 .
.
б) Применяем тригонометрическую формулу 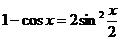 :
:
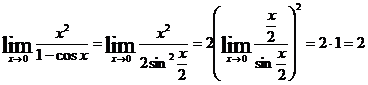 .
.
7. Установим, что при указанном изменении аргумента функция представляет произведение бесконечно малой величины на бесконечно большую (случай 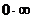 ), преобразуем ее к виду дроби, числитель и знаменатель которой одновременно стремятся к нулю или бесконечности.
), преобразуем ее к виду дроби, числитель и знаменатель которой одновременно стремятся к нулю или бесконечности.
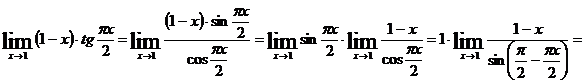
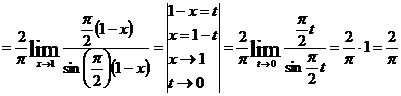 .
.
8. Убедившись сначала, что при указанном изменении аргумента функция представляет степень, основание которой стремится к единице, а показатель – к бесконечности (случай 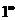 ), далее преобразуем функцию так, чтобы использовать 2-й замечательный предел.
), далее преобразуем функцию так, чтобы использовать 2-й замечательный предел.
Исключив целую часть из дроби, полагаем 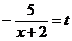
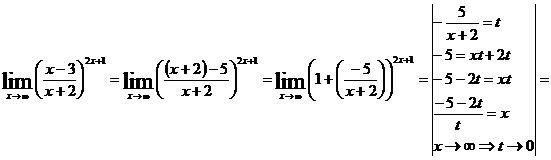
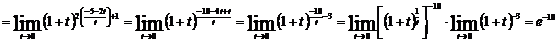 .
.
Задание 2. Найти производные функций:
1. 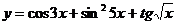
2. 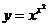
3. 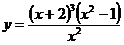
4. 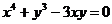
5. 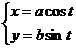 . Найти
. Найти 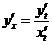 ,
, 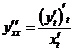
Решение:
1. 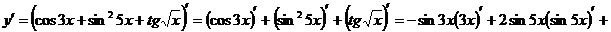
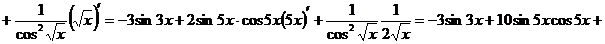
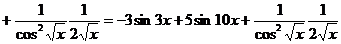
2. 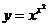
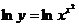
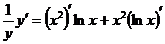
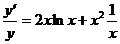
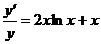
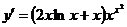
3. 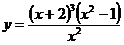
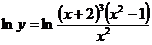
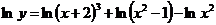
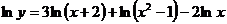
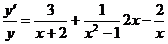
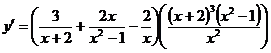
4. Составляя производную левой части равенства и приравнивая ее к нулю, получим:
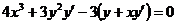
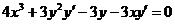
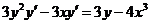
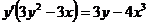
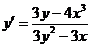
5. 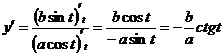
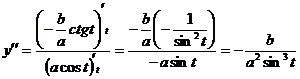 .
.
Задание 3. Используя геометрический смысл производной (производная равна угловому коэффициенту k = tgα касательной к графику функции f(x) в точке x0(f'(x0) = k = tgα)), составить уравнения касательной и нормали к заданной кривой y = x2 + х - 1 при x = x0 = 3.
Решение: Уравнение касательной к графику заданной функции в точке М(х0,у0), где 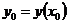 , имеет вид
, имеет вид 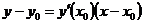 . Уравнение нормали в той же точке имеет вид
. Уравнение нормали в той же точке имеет вид 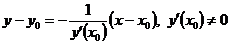 . Находим производную в точке х = 3:
. Находим производную в точке х = 3: 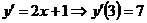 . Уравнение касательной имеет вид
. Уравнение касательной имеет вид 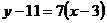 . Уравнение нормали имеет вид
. Уравнение нормали имеет вид 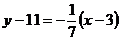 .
.
Задание 4. По правилу Лопиталя раскрытия неопределенностей найти пределы заданных функций:
1. 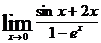
2. 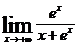
3. 
4. 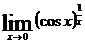
Решение:
1. Числитель и знаменатель стремятся к нулю при х→0, имеем неопределенность вида  .Применяя правило Лопиталя, получим
.Применяя правило Лопиталя, получим
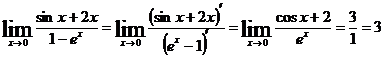 .
.
2. Это – неопределенность вида 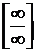 .Применив правило Лопиталя последовательно два раза, получим
.Применив правило Лопиталя последовательно два раза, получим
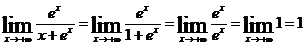 .
.
3. Имеем неопределенность вида [ 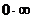 ]. Представим произведение функций в виде частного
]. Представим произведение функций в виде частного 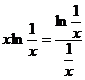 . Тогда будем иметь
. Тогда будем иметь 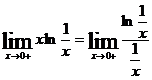 . Это - неопределенность вида
. Это - неопределенность вида 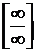 . Применяя далее правило Лопиталя, получим
. Применяя далее правило Лопиталя, получим
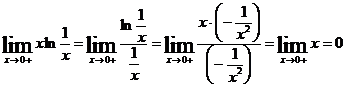 .
.
4. Имеем неопределенность вида [ 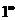 ]. Обозначим заданную функцию через у, т.е.
]. Обозначим заданную функцию через у, т.е. 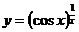 , и прологарифмируем ее.
, и прологарифмируем ее.
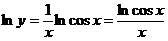 .
.
Вычислим предел логарифма данной функции 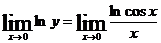 .
.
Это - неопределенность вида  . Применяя далее правило Лопиталя, получим
. Применяя далее правило Лопиталя, получим
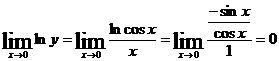 . Поэтому в силу непрерывности показательной функции
. Поэтому в силу непрерывности показательной функции 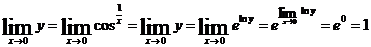 .
.
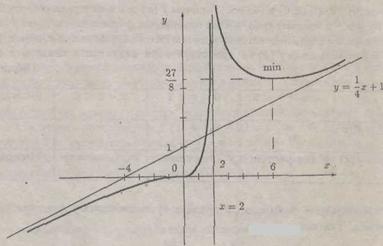
Задание 5. Исследовать функцию 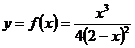 и построить её график методами дифференциального исчисления.
и построить её график методами дифференциального исчисления.
Решение: Функция определена при всех 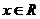 , кроме х = 2; её график пересекает оси координат в одной точке (0,0).
, кроме х = 2; её график пересекает оси координат в одной точке (0,0).
Функция положительна при х > 0, х ≠ 2 и отрицательна при х < 0.
Функция разрывна в точке х = 2, и поскольку 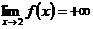 , прямая х = 2 – вертикальная асимптота графика.
, прямая х = 2 – вертикальная асимптота графика.
Из того, что 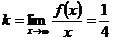 ,
, 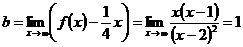 следует, что при х→∞ график имеет наклонную асимптоту
следует, что при х→∞ график имеет наклонную асимптоту 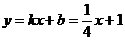 .
.
Используем необходимый признак экстремума. Вычислив первую производную 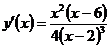 и приравнивая её нулю
и приравнивая её нулю 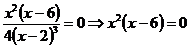 , находим критические точки х1 = 0; х2 = 6.
, находим критические точки х1 = 0; х2 = 6.
Экстремумы могут быть только в этих точках. Чтобы выявить, реализуются ли экстремумы в этих точках, используем второй достаточный признак экстремума. Так как 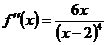 ,
, 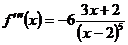 и
и 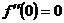 ,
, 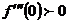 , то в точке х = х1 = 0 функция не имеет экстремума. Так как
, то в точке х = х1 = 0 функция не имеет экстремума. Так как 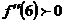 , то точка х = х2 = 6 является точкой минимума,
, то точка х = х2 = 6 является точкой минимума, 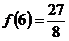 .
.
Точки х = 0, х = 2, х = 6 разбивают числовую ось на интервалы (-∞,0), (0,2), (2,6) и (6, +∞), причем 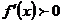 в интервалах (-∞,0), (0,2) и (6,+∞), следовательно, в этих интервалах функция возрастает;
в интервалах (-∞,0), (0,2) и (6,+∞), следовательно, в этих интервалах функция возрастает; 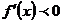 в интервале (2,6), следовательно, в этом интервале функция убывает. В точке х = 2 производная
в интервале (2,6), следовательно, в этом интервале функция убывает. В точке х = 2 производная 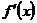 не существует. Эти результаты сведены в таблице.
не существует. Эти результаты сведены в таблице.
| x | -∞ < x < 0 | 0 < x < 2 | 2 < x < 6 | 6 < x < +∞ |
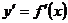 | + | + | - | + |
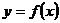 |  (возрастает) (возрастает) |  (возрастает) (возрастает) |  (убывает) (убывает) |  (возрастает) (возрастает) |
Используем необходимый признак существования у функции точек перегиба. Так как 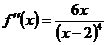 ,
, 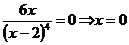 , то точкой перегиба функции может быть только х = 0. Чтобы выявить, является ли точка х = 0 точкой перегиба функции, используем второй достаточный признак существования у функции точки перегиба. Поскольку
, то точкой перегиба функции может быть только х = 0. Чтобы выявить, является ли точка х = 0 точкой перегиба функции, используем второй достаточный признак существования у функции точки перегиба. Поскольку 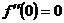 ,
, 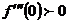 , то х = 0 является точкой перегиба функции.
, то х = 0 является точкой перегиба функции.
При 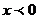
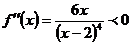 , следовательно, функция выпукла вверх, поэтому её график при х→-∞ приближается к асимптоте снизу. При
, следовательно, функция выпукла вверх, поэтому её график при х→-∞ приближается к асимптоте снизу. При 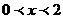 и при
и при 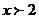
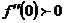 , следовательно, функция выпукла вниз. Отсюда следует, что при х→+∞ график приближается к асимптоте сверху. В точке х = 2 вторая производная – бесконечная. Эти результаты сведены в таблице.
, следовательно, функция выпукла вниз. Отсюда следует, что при х→+∞ график приближается к асимптоте сверху. В точке х = 2 вторая производная – бесконечная. Эти результаты сведены в таблице.
| x | -∞ < x < 0 | 0 < x < 2 | 2 < x < 6 |
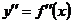 |  - - | 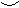 + + |  + + |
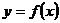 | (выпукла вверх) | (выпукла вниз) | (выпукла вниз) |
Вычислив ещё несколько точек графика, на основе произведенного исследования делаем более точный рисунок.
Задание 6. Найти наибольшее и наименьшее значения заданной функции 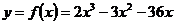 на отрезке
на отрезке 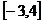 .
.
Решение: Наибольшее (наименьшее) значение непрерывной функции достигается или в критических точках функции внутри отрезка или на концах отрезка.
Находим критические точки функции
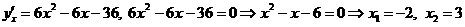 .
.
Обе критические точки лежат внутри заданного отрезка 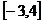 . Находим значения функции в точках
. Находим значения функции в точках 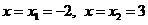 , а также на концах отрезка
, а также на концах отрезка 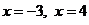 :
: 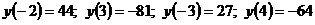 .
.
Следовательно, наибольшее значение функции 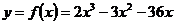 на отрезке
на отрезке 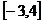 равно
равно 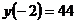 , наименьшее значение равно
, наименьшее значение равно 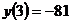 .
.
Контрольная работа №4
Функции многих переменных.
Задание 1.Найти области определения функций.
1. 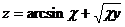
2. 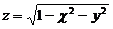
3. 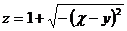
4. 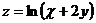
5. 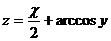
6. 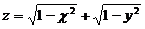
7. 
8. 
9. 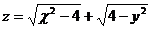
10. 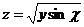
11. 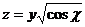
12. 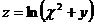
13. 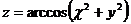
14. 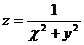
15. 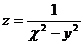
16. 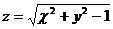
17. 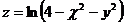
18. 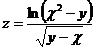
19. 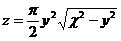
20. 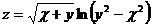
21. 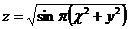
22. 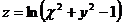
23. 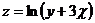
24. 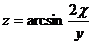
25. 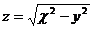
26. 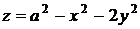
27. 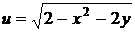
28. 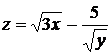
29. 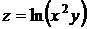
30. 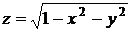
Задание 2.Найти частные производные 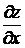 и
и 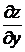 заданной функции
заданной функции 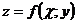 .
.
1. 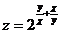
2. 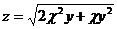
3. 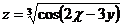
4. 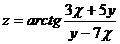
5. 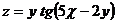
6. 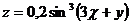
7. 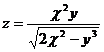
8. 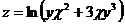
9. 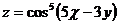
10. 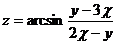
11. 
12. 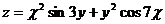
13. 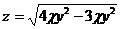
14. 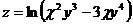
15. 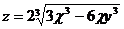
16. 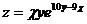
17. 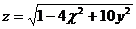
18. 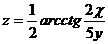
19. 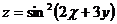
20. 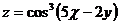
21. 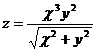
22. 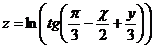
23. 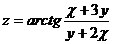
24. 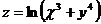
25. 
26. 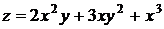
27. 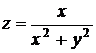
28. 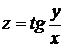
29. 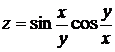
30. 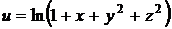
Задание 3.Найти полные дифференциалы I и II порядков данных функций.
1. 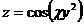
2. 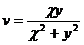
3. 
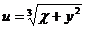
4. 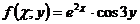
5. 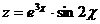
6. 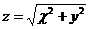
7. 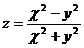
8. 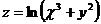
9. 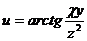
10. 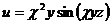
11. 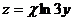
12. 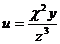
13. 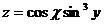
14. 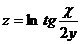
15. 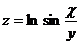
16. 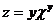
17. 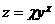
18. 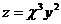
19. 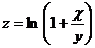
20. 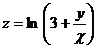
21. 
22. 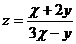
23. 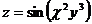
24. 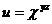
25. 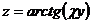
26. 
27. 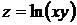
28. 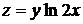
29. 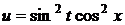
30. 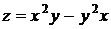
Задание 4.Дифференцирование сложных функций.
1. Найти 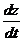 , если
, если 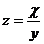 , где
, где 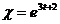 ,
, 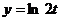 .
.
2. Найти 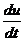 , если
, если 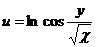 , где
, где 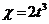 ,
, 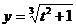 .
.
3. Найти 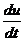 , если
, если 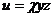 , где
, где 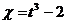 ,
, 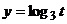 ,
, 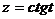 .
.
4. Найти 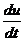 , если
, если 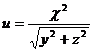 , где
, где 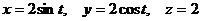 .
.
5. Найти 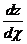 , если
, если 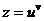 , где
, где 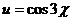 ,
, 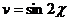 .
.
6. Найти 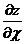 и
и 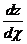 , если
, если 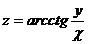 и
и 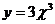 .
.
7. Найти 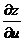 и
и 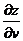 , если
, если  , где
, где 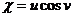 ,
, 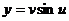 .
.
8. Найти 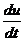 , если
, если 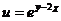 , где
, где 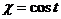 ,
, 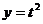 .
.
9. Найти 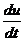 , если
, если 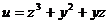 , где
, где 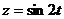 ,
, 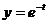 .
.
10. Найти 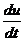 , если
, если 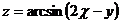 , где
, где 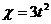 ,
, 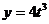 .
.
11. Найти 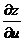 и
и 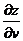 , если
, если 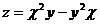 , где
, где 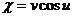 ,
, 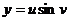 .
.
12. Найти 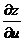 и
и 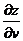 , если
, если 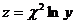 , где
, где 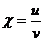 ,
, 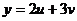 .
.
13. Найти 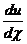 , если
, если  , где
, где 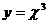 .
.
14. Найти 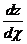 , если
, если 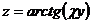 , где
, где 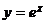 .
.
15. Найти 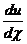 , если
, если  , где
, где 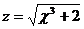 .
.
16. Найти 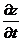 , если
, если 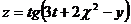 , где
, где 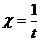 ,
, 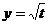 .
.
17. Найти 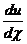 , если
, если 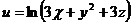 , где
, где 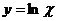 ,
, 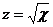 .
.
18. Найти 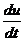 , если
, если 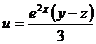 , где
, где 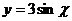 ,
, 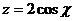 .
.
19. Найти 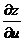 и
и 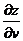 , если
, если 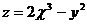 , где
, где 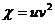 ,
, 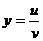 .
.
20. Найти 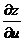 и
и 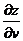 , если
, если 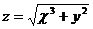 , где
, где 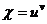 ,
, 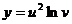 .
.
21. Найти 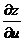 и
и 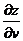 , если
, если 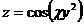 , где
, где 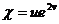 ,
, 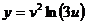 .
.
22. Найти 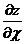 и
и 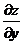 , если
, если 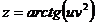 , где
, где 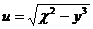 ,
, 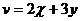 .
.
23. Найти 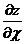 и
и 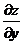 , если
, если 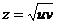 , где
, где 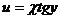 ,
, 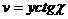 .
.
24. Найти 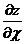 и
и 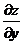 , если
, если 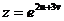 , где
, где 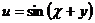 ,
, 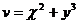 .
.
25. Найти 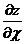 и
и 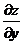 , если
, если 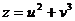 , где
, где 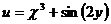 ,
, 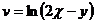 .
.
26. Найти 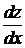 , если
, если 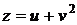 , где
, где 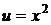 ,
, 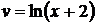 .
.
27. Найти 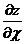 и
и 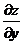 , если
, если 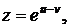 где
где 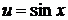 ,
, 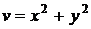 .
.
28. Найти 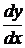
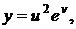 где
где 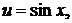
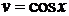 .
.
29. Найти 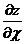 ,
, 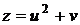 , где
, где 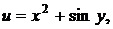
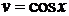 .
.
30. Найти 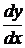 ,
, 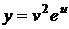 где
где 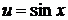 ,
, 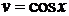 .
.
Задание 5.Найти частные производные второго порядка функции 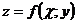 .
.
1. 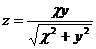
2. 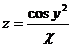
3. 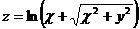
4. 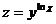
5. 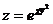
6. 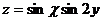
7. 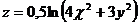
8. 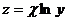
9. 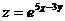
10. 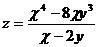
11. 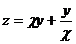
12. 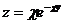
13. 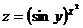
14. 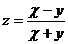
15. 
16. 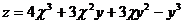
17. 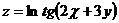
18. 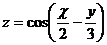
19. 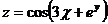
20. 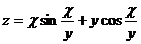
21. Дана функция 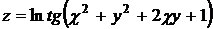 .
.
Показать, что 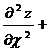
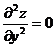
22. Дана функция z = e x y . Показать, что 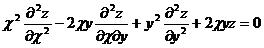
23. Дана функция 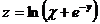 . Показать, что
. Показать, что 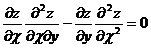
24. Дана функция 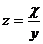 . Показать, что
. Показать, что 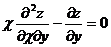
25. Дана функция 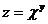 . Показать, что
. Показать, что 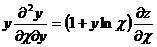
26. 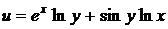
27. 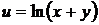
28. 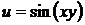
29. 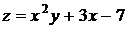
30. 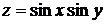
Задание 6.Найти производную неявной функции от х, заданную уравнением в точке с координатами 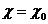 ,
, 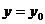 .
.
1. 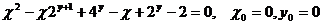
2. 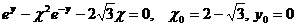
3. 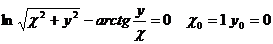
4. 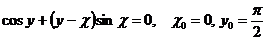
5. 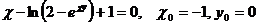
6. 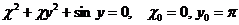
7. 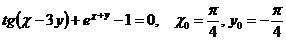
8. 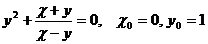
9. 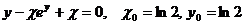
10. 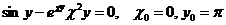
11. Найти 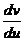 , если
, если 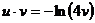
12. Найти 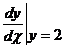 , если
, если 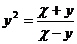
13. Найти 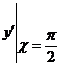 , если
, если 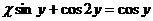
14. Найти 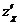 ,
, 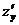 , если
, если 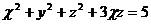
15. Проверить, что функция 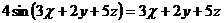 удовлетворяет уравнению
удовлетворяет уравнению 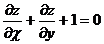 .
.
Найти производную неявной функции:
16. 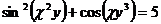
17. 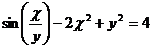
18. 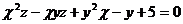
19. 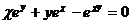
20. 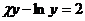
21. 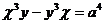
22. 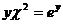
23. 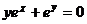
24. 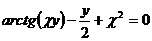
25. 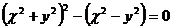
26. 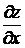 и
и 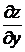 , если
, если 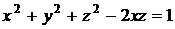
27. 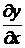 , если
, если 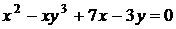
28. 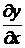 , если
, если 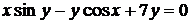
29. 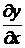 , если
, если 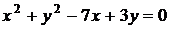
30. 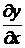 , если
, если 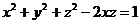
Задание 7.Найти градиент функции в точке М.
1.  | 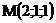 |
2. 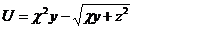 | 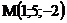 |
3. 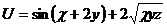 | 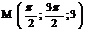 |
4. 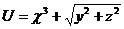 | 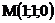 |
5. 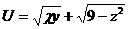 | 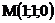 |
6. 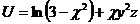 | 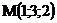 |
7. 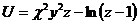 | 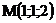 |
8. 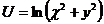 | 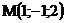 |
9. 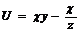 | 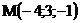 |
10. 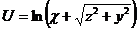 | 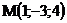 |
11. 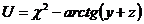 | 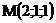 |
12. 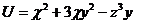 | 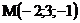 |
13. 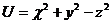 | 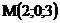 |
14. 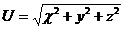 | 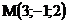 |
15. 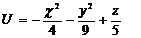 | 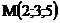 |
16. 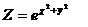 | 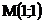 |
17. 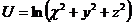 | 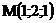 |
18. 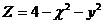 | 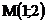 |
19. 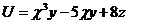 | 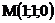 |
20. 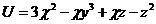 | 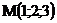 |
21. 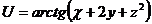 | 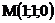 |
22.  | 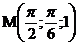 |
23. 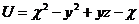 | 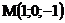 |
24. 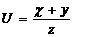 | 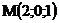 |
25. 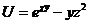 | 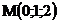 |
26. 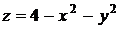 | 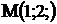 |
27. 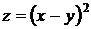 |
