Образец выполнения контрольной работы №2.

Задание 1.

а) Найти острый угол между двумя плоскостями .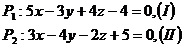

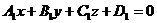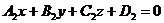Решение: Угол между двумя плоскостями и равен углу между их нормальными векторам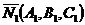и и 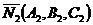и определяется по формуле

.

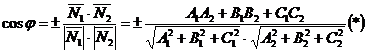Из формулы (*) получим, если учесть, что на основании уравнения (I) А₁ = 5; В₁ = 3; С₁ = 4, а из (II) А₂ = 3; В₂ = -4; С₂ = -2,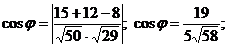

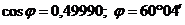. В формуле (*) следует взять абсолютную величину правой части, так как надо найти острый угол между плоскостями.

б) Составить уравнение плоскости, которая проходит через прямую пересечения плоскостей Р₁, Р₂ и точку М(2,-1,3).

Решение: Две пересекающиеся плоскости Р₁ и Р₂ определяют (задают) пучок плоскостей, уравнение которого имеет вид 5x–3y+4z–4+t (3x–4y–2z+5)=0, где t – параметр. Все плоскости этого пучка проходят через прямую пересечения плоскостей Р₁ и Р₂ (ось пучка). Из множества плоскостей пучка выбираем ту (определяем значение t), которая проходит через точку М: значение t должно быть таким, чтобы координаты точки М удовлетворяли уравнению

.

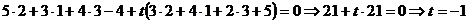Уравнение искомой плоскости

.

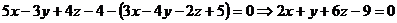Задание 2. Даны уравнения высот треугольника 2х – 3у + 1 = 0 и х + у = 0 и координаты одной из его вершин А(1;2). Найти уравнения сторон треугольника.

Решение: Точка А(1;2) не принадлежит данным в условии высотам треугольника, так как ее координаты не удовлетворяют их уравнениям:

2·1 - 3·2 + 1 ≠ 0 и 1 + 2 ≠ 0. Отсюда следует, что высоты, данные в задаче, проведены из двух других вершин треугольника В и С. Назовем их СД и ВЕ, 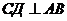, 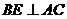. Пусть высота СД имеет уравнение х + у = 0, а высота ВЕ имеет уравнение 2х – 3у + 1 = 0.

I способ. Так как 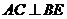, то уравнение АС мы найдем из уравнения семейства прямых, перпендикулярных ВЕ, приняв во внимание, что искомая прямая проходит через данную точку А(1;2).

Если две прямые 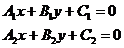перпендикулярны, то выполняется условие 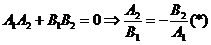, то есть коэффициенты при х и у меняются местами, а также изменяется знак при у.

1. Уравнение стороны АС

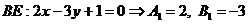
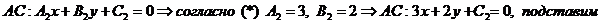
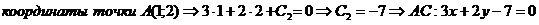
2. Уравнение стороны АВ

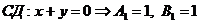
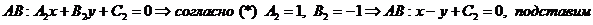
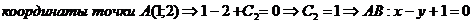
3. Уравнение стороны ВС

Сначала следует найти координаты точек В и С, как точек пересечения прямых ВЕ и АВ и прямых СД и АС, соответственно.

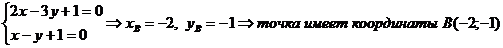
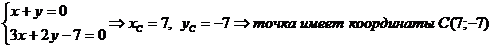
Теперь найдем уравнение ВС, воспользовавшись уравнение прямой, проходящей через две точки В(-2;-1) и С(7;-7).

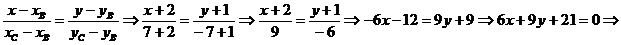
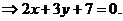
II способ. Если две прямые заданы уравнениям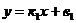и и 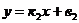, то условия перпендикулярности двух прямых имеет вид .

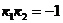1. Уравнение стороны АС ( )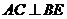

Определим угловой коэффициент 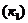высоты ВЕ. Преобразуем уравнение высоты ВЕ: .

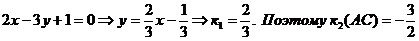Уравнение прямой, проходящей через данную точку А(х₁;у₁) в данном направлении, определяемом угловым коэффициентом, (**).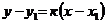

Точка А(1;2) принадлежит прямой АС, поэтому подставим ее координаты в уравнение (**). .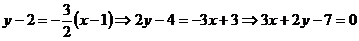

2. Уравнение стороны АВ ( )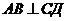

Угловой коэффициент высоты СД, имеющей вид, 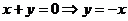равен .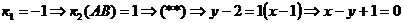

3. Уравнение стороны ВС рассмотрено выше.

Задание 3. Найти уравнение касательной к параболе у² = 4х, проведенной из точки А(-2;-1).

Решение: Уравнение прямой будем искать в виде 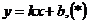. Так как точка А принадлежит искомой касательной, подставляя ее координаты в уравнение (*), получим тождество 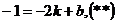. Далее, прямая (*) и парабола у² = 4х имеют единственную общую точку (касаются). Следовательно, система уравнений 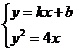имеет единственное решение. Решаем ее относительно

х и у. Это можно сделать различными способами, например, возвести правую и левую части первого уравнения в квадрат и подставить в левую часть полученного равенства вместо у² его выражение из второго уравнения. Получим 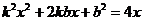. Это – квадратное уравнение, имеющее единственное решение в случае, когда дискриминант равен нулю. Таким образом, . Теперь для параметров k и b прямой (*) имеем два условия: (**) и (***). Следовательно, искомые значения параметров находятся как решения системы из этих условий:

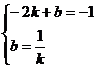. Подстановкой вместо b в первое уравнение его выражения из второго, получим 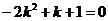, откуда находим, что 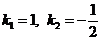. Система имеет два решения: 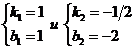. Следовательно, две прямые удовлетворяют условиям задачи. Их уравнения: .

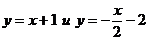Задание 4. Постройте кривую 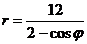в полярной системе координат. Найти каноническое уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс - с полярной осью.

Решение: Полярная система координат задана, если заданы точка О, называемая полюсом, и исходящий из полюса луч ОР- полярная ось. Если задать на плоскости прямоугольную декартову систему координат, поместив ее начало в полюс и совместив ось абсцисс с полярной осью, то декартовы координаты х и у будут выражены через полярные координаты (r и φ) уравнениями:

.

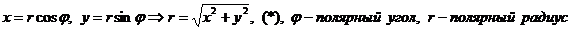Составим таблицу для значений r от φ с шагом π/8.

φ		π/8	π/4	3π/8	π/2	5π/8	3π/4	7π/8	π
cosφ		0,92	0,71	0,38		-0,38	-0,71	-0,92	-1
r		11,1	9,3	7,4			4,4	4,1
φ	9π/8	5π/4	11π/8	3π/2	13π/8	7π/4	15π/8	2π
cosφ	-0,92	-0,71	-0,38		0,38	0,71	0,92
r	4,1	4,4			7,4	9,3	11,1

Примем произвольный отрезок за единицу масштаба, которым мы будем пользоваться при построении r. Для построения проводим из полюса лучи, соответствующие выбранным значениям φ, и на каждом луче (то есть вдоль него) откладываем соответствующие вычисленные значения полярного радиуса. Полученные точки соединяем плавной кривой. Построенная линия – эллипс.

Найдем каноническое уравнение данной линии в декартовой прямоугольной системе координат, используя уравнения, отмеченные выше (*).

.

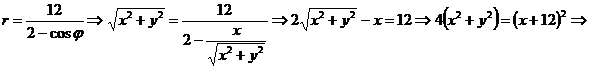
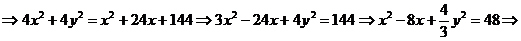
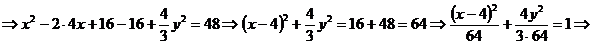
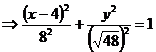Это уравнение определяет эллипс с полуосями 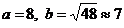и с центром симметрии О(4,0).

Контрольная работа №3