Тема 8. ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

Вопросы для самопроверки

1. Дайте определение функции двух независимых переменных. Объясните геометрический смысл функции двух переменных.

2. Объясните, что понимают под областью определения функции двух переменных, как изображают область определения геометрически.

3. Дайте определение частных производных функции двух переменных.

4. Дайте определение частного и полного дифференциалов функции двух переменных.

5. Дайте определение максимума (минимума) функции двух переменных.

6. Какие точки называются критическими? Как они находятся?

7. Сформулируйте необходимые условия экстремума функции двух переменных.

8. Сформулируйте достаточные условия функции двух переменных.

Рекомендации к решению заданий

1. Найдем область определения функции

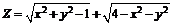
и изобразим ее геометрически.

Область определения данной функции определяется системой неравенств

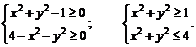
Построим границы области определения:

х²+у²=1 – окружность R=1, центр (0;0);

х²+у²=4 – окружность R=2, центр (0;0);

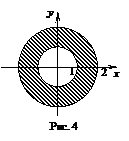
х²+у²³1 – окружность R=2, центр (0;0);

x²+y²³1 – внешняя часть круга радиуса 1;

x²+y²£4 – внутренняя часть круга радиуса 2.

Областью определения данной функции является изображенное кольцо, границы которого входят в область определения функции.

2. Исследуем данную функцию на экстремум: Z=2x²–xy+y²–3x–y+1; xÎR, yÎR.

Найдем частные производные первого порядка:

; .

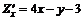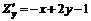Найдем стационарные точки: 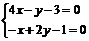, откуда x=1, y=2.

Таким образом, стационарной точкой функции является М(1; 2).

Проверим достаточные условия существования экстремума функции. Для этого найдем значения частных производных второго порядка:

; ; .

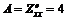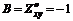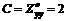Составим выражение AC–B²=4×2–(–1)²=7>0 – экстремум существует. Так как А=4>0, то функция в точке М имеет минимум.

Z_min(1; 2) = 2×1²–1×2+2² –3×1–2+1=2–2+4–3–2+1=0, Z_min=0.

Задание 11

Задачи 201-220.Найти область определения функции двух переменных и изобразить ее геометрически.

201. 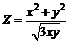.	202. .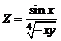
203. 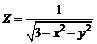.	204. .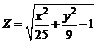
205. 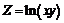.	206. .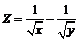
207. 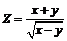.	208. .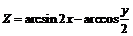
209. Z=arcsin (x + y).	210. Z=arcсos (x – y).
211. 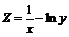.	212. .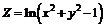
213. 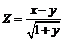.	214. .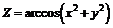
215. 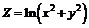.	216. .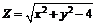
217. 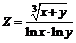.	218. .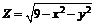
219. 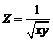.	220. .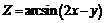

Задание 12

Задачи 221–240.Исследовать на экстремум функции.

221. .
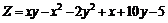222. .
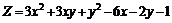223. .
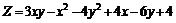224. .
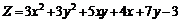225. .
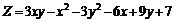226. .
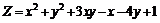227. .
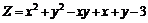228. .
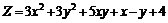229. .
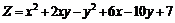230. .
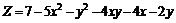231. .
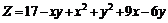232. .
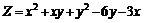233. .
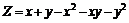234. .
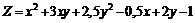235. .
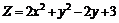236. .
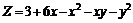237. .
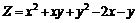238. .
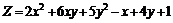239. .
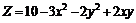240. .

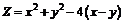Тема 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

Вопросы для самопроверки

1.Сформулировать теорему существования и единственности решения дифференциального уравнения.

2. Что называется общим решением, частным решением дифференциального уравнения?

3. Какой вид имеет дифференциальное уравнение с разделяющимися переменными?

4. Какой вид имеет общее решение линейного однородного уравнения второго порядка?

Рекомендации к решению заданий

1. Найдем частное решение дифференциального уравнения 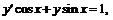удовлетворяющее начальному условию у(0)=0.

Заданное уравнение является линейным. Полагаем 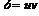и 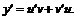Подставим 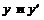в исходное уравнение, получим

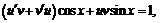
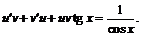
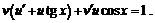(1)

Подберем функцию 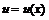так, чтобы выражение, содержащиеся в скобках, обращалось в нуль:

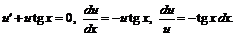
После интегрирования получим 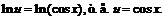При 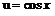равенство (1) обратится в уравнение

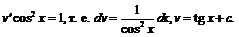
Общее решение исходного уравнения будет 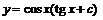или 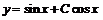. Используя начальные условия, вычислим соответствующее ему значение постоянной С: .

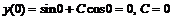Тогда частное решение имеет вид у=sin x.

2. Найдем частные решения линейных однородных уравнений второго порядка:

a) ;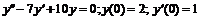

б) ;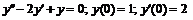

в) .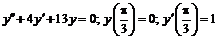

a) составим характеристическое уравнение 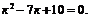Корни этого уравнения 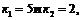поэтому общее решение записывается в виде 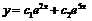. Чтобы получить частное решение, необходимо подставить начальные данные в выражение для 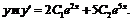Получим 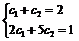, откуда 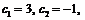следовательно, искомое решение будет иметь вид ;

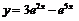б) cоставим характеристическое уравнение к²–2к+1=0. Оно имеет два равных корня к₁=к₂=1, тогда общее решение записывается в виде у=с₁ е^х+с₂хе^х, откуда 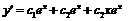. Учитывая начальные условия, получим 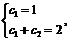откуда с₂=1. Искомое частное решение будет иметь вид у =е^х+хе^х;

в) cоставим характеристическое уравнение к²+4к +13=0. Это уравнение не имеет вещественных корней. Тогда общее решение записывается в виде .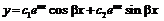

В нашем случа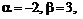е т. е. .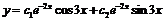

Для нахождения частного решения дифференциального уравнения вычислим первую и вторую производные от найденного общего решения: .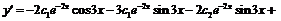

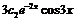Воспользовавшись заданными начальными условиями, получим:

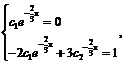откуда с₁ = 0, .

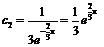Частное решение будет иметь вид .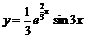

Задание 13

Задачи 241–260. Найти: а) частное решение дифференциального уравнения первого порядка; б) частное решение линейного однородного уравнения второго порядка.

241. ; .	; .
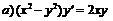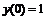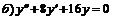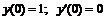242. ; .	.
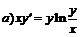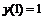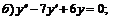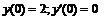243. ; .	.
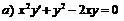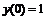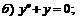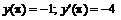244. ; .	.
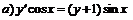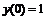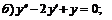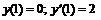245. .	.
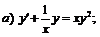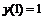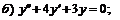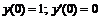246. ; .	.
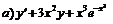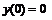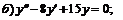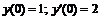247. а) .	.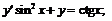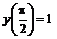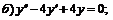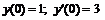
248. .	.
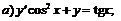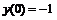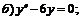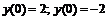249.	.
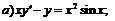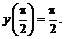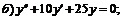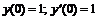250. ; .	.
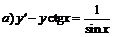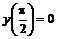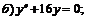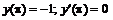251.	.
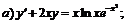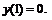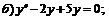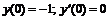252.	.
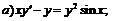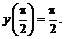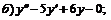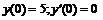253.	.
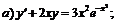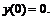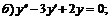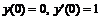254.	.
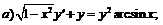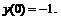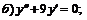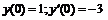255.	.
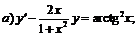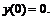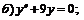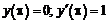256.	.
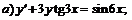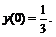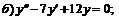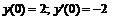257. .	.
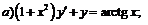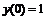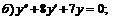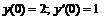258.	.
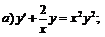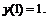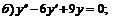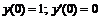259.
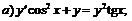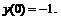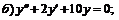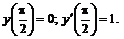260.

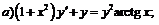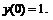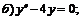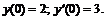Тема 10. РЯДЫ

Вопросы для самопроверки

1. Какой ряд называется сходящимся ( расходящимся)?

2. Сформулировать необходимое условие сходимости ряда.

3. В чем состоит признак Даламбера?

4. Для каких рядов применяется признак Лейбница? В чем его сущность?

5. Как найти радиус сходимости степенного ряда?

6. Как используются степенные ряды в приближенных вычислениях?

Рекомендации к решению заданий

1. Исследуем на сходимость ряд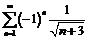. Для этого рассмотрим абсолютные величины членов исходного ряда .

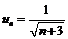При этом 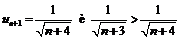или 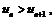поэтому члены заданного ряда монотонно убывают по абсолютной величине. Кроме того, 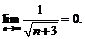Выполнены все условия признака Лейбница, следовательно ряд сходится.

2. Найдем радиус сходимости степенного ряда 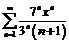и определим характер сходимости ряда на концах интервала сходимости. По формуле 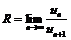найдем радиус сходимости:

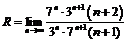
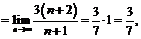
где 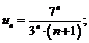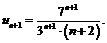Тогда в интервале 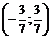ряд сходится абсолютно. Выясним вопрос сходимости ряда на концах интервала, т. е. в точках 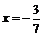, 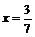. При 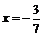заданный ряд принимает вид

.

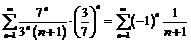Это числовой знакочередующийся ряд. Его общий член по абсолютной величине монотонно убывает и стремится к нулю при n®¥. Таким образом, все условия признака Лейбница выполнены и ряд сходится, т.е. точка 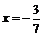принадлежит области сходимости заданного ряда. При 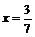исходный ряд принимает вид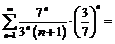

.

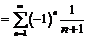Это числовой знакоположительный ряд, который, очевидно, расходится (сравните его с гармоническим рядом). Следовательно, точка 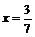не принадлежит области сходимости заданного ряда. Таким образом, область сходимости данного степенного ряда 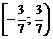. Вне этого интервала ряд расходится.

Задание 14

Задачи 261–280. Требуется: а) исследовать на сходимость с помощью признака Лейбница знакочередующийся ряд; б) найти радиус сходимости степенного ряда и определить тип сходимости ряда на концах интервала сходимости.

261.	.
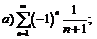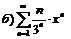262.	.
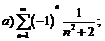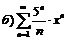263.	.
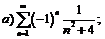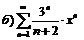264.	.
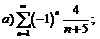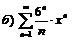265.	.
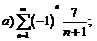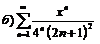266.	.
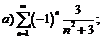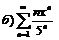267.	.
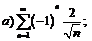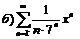268.	.
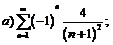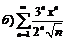269.	.
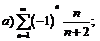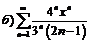270.	.
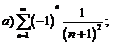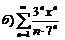271.	.
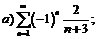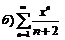272.	.
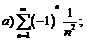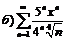273.	.
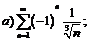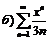274.	.
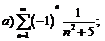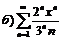275.	.
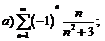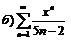276.	.
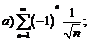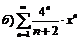277.	.
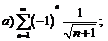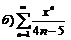278.	.
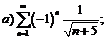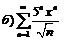279.	.
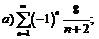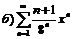280.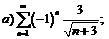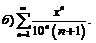