Основные виды рычажных механизмов.
Лекция 1.
Основные понятия и определения.
Теория механизмов и машин занимается исследованием и разработкой высокопроизводительных механизмов и машин.
Механизм– совокупность подвижных материальных тел, одно из которых закреплено, а все остальные совершают вполне определенные движения, относительно неподвижного материального тела.
Звенья – материальные тела, из которых состоит механизм.
Стойка– неподвижное звено.
 Стойка изображается ; конфигурация стойки в курсе ТММ не изучается. Звено, к которому изначально сообщается движение, называется входным (начальным, ведущим). Звено, совершающее движение, для выполнения которого предназначен механизм – выходное звено.
Стойка изображается ; конфигурация стойки в курсе ТММ не изучается. Звено, к которому изначально сообщается движение, называется входным (начальным, ведущим). Звено, совершающее движение, для выполнения которого предназначен механизм – выходное звено.
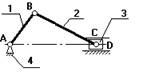
Кривошипно-
Ползунный
Механизм
Рис.1
Если это компрессор, то зв.1 – входное, а зв.3 – выходное.
Если это механизм ДВС, то зв.3 – входное, а зв.1 – выходное.
Кинематическая пара– подвижное соединение звеньев, допускающее их относительное движение. Все кинематические пары на схеме обозначают буквами латинского алфавита, например A, B, C и т.д.

 Если , то К.П. – вращательная ; если , то поступательная.
Если , то К.П. – вращательная ; если , то поступательная.
Порядок нумерации звеньев:
входное звено – 1;
стойка – последний номер.
Звенья бывают:
· простые – состоят из одной детали;
· сложные – состоят из нескольких, жестко скрепленных друг с другом и совершающих одно и тоже движение.
Например, шатунная группа механизма ДВС.
Звенья, соединяясь друг с другом, образуют кинематические цепи, которые разделяют на:
· простые и сложные;
· 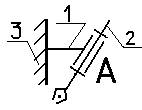 замкнутые и разомкнутые;
замкнутые и разомкнутые;
Пример замкнутой кинематической
цепи на рис.1;
пример разомкнутой цепи:
Машина – техническое устройство, в результате осуществления технологического процесса определенного рода, можно автоматизировать или механизировать труд человека.
Машины условно можно разделить на виды:
· энергетические;
· технологические;
· транспортные;
· информационные.
Энергетические машины разделяют на:
· двигатели;
· трансформирующие машины.
Двигатель – техническое устройство, преобразующее один вид энергии в другой. Например, ДВС.
Трансформаторная машина – техническое устройство, потребляющее энергию извне и совершающее полезную работу. Например, насосы, станки, прессы.
Техническое объединение двигателя и технологической (рабочей машины) – Машинный агрегат (МА).
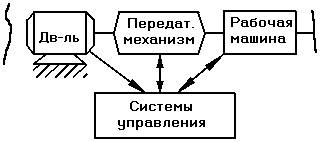
Внешняя Технологический среда процесс
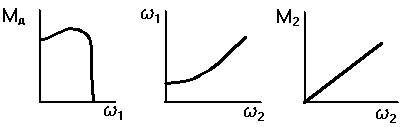 |
Двигатель имеет определенную механическую характеристику, рабочая машина тоже. Механические характеристики указаны в техпаспорте.
w1 – скорость, с которой вращается вал двигателя;
w2 – скорость, с которой будет вращаться главный вал рабочей машины.
w1 и w2 нужно поставить в соответствие друг другу.
Например, число оборотов n1 =7000 об/мин., а n2=70 об/мин.
Чтобы привести в соответствие механические характеристики двигателя и рабочей машины, между ними устанавливают передаточный механизм, который имеет свои механические характеристики.
up2=w1/w2=700/70=10
В качестве передаточного механизма могут быть использованы:
· фрикционные передачи (с использованием трения);
· цепные передачи (привод мотоцикла);
· зубчатые передачи.
В качестве рабочей машины наиболее часто используют рычажные механизмы.
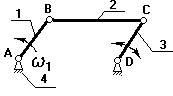
Рис. 2
1-кривошип, т.к. звено совершает полный оборот вокруг своей оси;
2-шатун, не связан со стойкой, совершает плоское движение;
3-ползун (поршень), совершает поступательное движение;
4-стойка.
 |
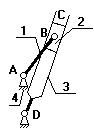
2. Четырехшарнирный механизм.
Звенья 1,3 могут быть кривошипами.
Если зв.1,3 – кривошипы, то механизм двукривошипный.
Если зв.1 – кривошип (совершает полный оборот), а зв.3 – коромысло (совершает неполный оборот), то механизм кривошипно-коромысловый.
Если зв.1,3 – коромысла, то механизм двукоромысловый.
3. Кулисный механизм.
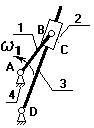 |
1 - кривошип;
2 - камень кулисы (втулка) вместе с зв.1 совершает полный оборот вокруг А (w1 и w2 одно и тоже), а также движется вдоль зв.3, приводя его во вращение;
3 - коромысло (кулиса).
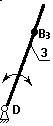
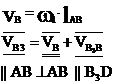 |
на зв.3 выбирают точку В3 и выбирают в данный момент так, чтобы она совпадала с точкой В.
4.Гидроцилиндр
(в кинематическом отношении подобен кулисному механизму).
 |
В процессе проектирования конструктор решает две задачи:
· анализа (исследует готовый механизм);
· синтеза (проектируется новый механизм по требуемым параметрам);
Лекция 2.
Глава 1. Анализ рычажных механизмов.
В данной главе будут рассмотрены вопросы:
1. структурный анализ механизма (изучение строения механизма);
2. изучение классов и видов кинематических пар.
3. определение числа степеней свободы механизма и определение наличия или отсутствия избыточных связей; в случае наличия – дать рекомендации по способу их устранения;
4. кинематический анализ механизма.
§1.1
Примечание:
Кинематическая пара существует, если не происходит деформации звеньев, образующих эту пару, и не должно происходить отрыва звеньев одно от другого, образующих кинематическую пару.
Примечание:
Ограничения, накладываемые на независимые движения звеньев, образующих кинематическую пару, называются – условия связи S.
Число степеней свободы механизма
W=S+H,
где Н – подвижность.
Любое незакрепленное тело в пространстве имеет 6 степеней свободы, на плоскости – 3.
Классификация кинематических пар проводят либо числу связей, либо по числу подвижностей:
Число связей Класс КП Число подвижностей
S=1 PI H=5
S=2 PII H=4
S=3 PIII H=3
S=4 PIV H=2
S=5 PV H=1
Существует 5 классов кинематических пар.
Примеры различных КП смотри рис. 4-95.
Кинематические пары по характеру контакта звеньев, образующих КП, разделяют на:
1. низшие:
· вращательные;
· поступательные;
2. высшие.
Контакт звеньев в низшей КП осуществляется по поверхности. Контакт звеньев в высшей КП – либо по линии, либо в точке.
§1.2 Определение числа степеней свободы рычажных механизмов.
1.2.1 Плоские механизмы.
В плоском механизме все звенья движутся в одной плоскости, все оси параллельны друг другу и перпендикулярны плоскости механизма.
ФОРМУЛА ЧЕБЫШЕВА: Wпп=3n -2pн -pв,
Где n – число подвижных звеньев механизма, рн – число низших КП, рв – число высших КП.
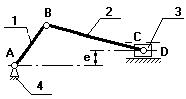
n=3
pн=4
рв=0
W=3.3-2.2=1
Рис.1.2.1
1.2.2 Пространственные механизмы.
В пространственном механизме оси непараллельны, звенья могут двигаться в разных плоскостях.
Wпр= 6n - (S1+ S2+ S3+ S4+ S5)
Допустим, что механизм, изображенный на рис.1.2.1 – пространственный и все кинематические пары 5-го класса, т.е. одноподвижны AV,BV,CV,DV, тогда
Wпр= 6n - (5pV+4pIV+3pIII+2pII+pI)
Wпр= 6.3 - 5.4 = -2 à статически неопределимая ферма.
Для получения Wдейств=0, необходимо добавить 3 движения.
q= Wдейств - Wпр = 1 - (-2) = 3,
где q – избыточные связи.
Для того чтобы их устранить, надо изменить класс некоторых кинематических пар, при этом нельзя изменять класс КП А. Поэтому, сделаем КП В – сферическим шарниром, т.е. 3-го класса (добавим 2 подвижности), а КП С – 4-го класса (добавим 1 подвижность). Тогда
Wпр= 6.3 - ( 5.2 + 4.1 + 3.1 ) = 18 - 17 = 1
n
ФОРМУЛА СОМОВА-МАЛЫШЕВА:Wпр= 6.n - ΣSi + q
i=1
§1.3 Кинематический анализ рычажных механизмов.
1.3.1 Основные понятия и определения.
Зависимость линейных координат в какой-либо точке механизма от обобщенной координаты – линейная функция положения данной точки в проекциях на соответствующие оси координат.
Хс= f(j1)
Зависимость угловой координаты какого-либо звена механизма от обобщенной координаты – угловая функция положения данного звена.
j2= f(j1)
Первая производная линейной функции положения точки по обобщенной координате – линейная передаточная функция данной точки в проекциях на соответствующие оси координат (иногда называют «аналог линейной скорости…»)
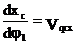
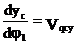
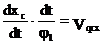
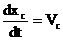

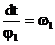
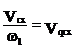
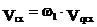
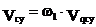
полная скорость т. С будет 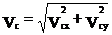
Первая производная угловой функции положения звена по обобщенной координате – передаточное отношение.
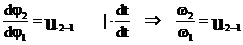
Вторая производная линейной функции положения по обобщенной координате – аналог линейного ускорения точки в проекциях на соответствующие оси.
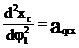
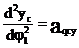
Вторая производная угловой функции положения звена по обобщенной координате – аналог углового ускорения звена.
1.3.2 Аналитический способ определения кинематических параметров рычажных механизмов.
Дано: w1, lAB, lBS2, lBC, lAC
Определить: vi, ai, w2, e2.
Для исследования плоских рычажных механизмов для решения данной задачи целесообразно использовать метод проецирования векторного контура на оси координат.
Для определения функции положения точки С представим длины звеньев в виде векторов.
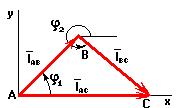 Условие замкнутости данного контура:
Условие замкнутости данного контура:
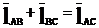 (1)
(1)
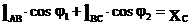 (2)
(2)
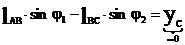
 (3)
(3)
рис.1.3.2 из (3) следует, что
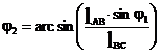 (4)
(4)
Лекция 3.
Продифференцируем (3) по обобщенной координате:
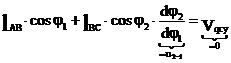
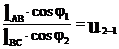 (5)
(5)
Продифференцируем (2) по обобщенной координате:
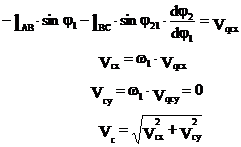
Если необходимо определить функции положения центра масс, то вы делим векторный контур ABS2
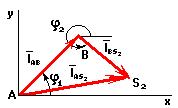 Условие замкнутости данного векторного контура имеет вид:
Условие замкнутости данного векторного контура имеет вид:

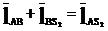 (6)
(6)
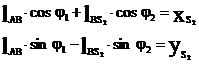 (7)
(7)
Продифференцируем (7) по обобщенной координате и получим аналоги линейных скоростей точек S2 в проекциях на оси х и у:
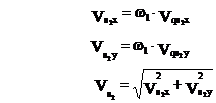 (9)
(9)
Глава 2. Анализ машинного агрегата.
В данной главе будут рассмотрены следующие вопросы:
1. Силы и моменты, действующие в машинном агрегате.
2. Переход от расчетных схем машинных агрегатов к динамическим моделям.
3. Расчет усилий в кинематических парах основного механизма рабочей машины.
4. Определение законов движения главного вала (входного звена) рабочей машины под действием приложенных сил и моментов при различных режимах работы машинного агрегата.
§2.1 Силы и моменты, действующие в машинном агрегате.
2.1.1 Движущиеся силы и моменты Fд и Мд.
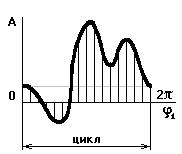 Работа движущих сил и моментов за цикл положительна: Ад>0.
Работа движущих сил и моментов за цикл положительна: Ад>0.
Цикл – промежуток времени, по истечению которого все кинематические параметры принимают первоначальное значение, а технологический процесс, происходящий в рабочей машине, начинает повторяться вновь.
2.1.2 Силы и моменты сопротивления (Fс,Mс).
Работа сил и моментов сопротивления за цикл отрицательна: Аc<0.
2.1.3 Силы тяжести (Gi).
Работа силы тяжести за цикл равна нулю: АGi=0.
2.1.4 Расчетные силы и моменты (ФSi,MФi).
ФSi,MФi – Главные векторы сил инерции и главные моменты от сил инерции.
2.1.5 Реакции в кинематических парах (Qij).
§2.2 Понятие о механических характеристиках.
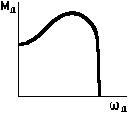
Механическая характеристика 3-х фазного асинхронного двигателя.
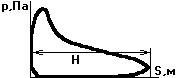
Индикаторная диаграмма ДВС
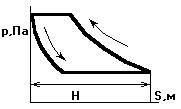
H – ход поршня в поршневой машине
(расстояние между крайними
положениями поршня)
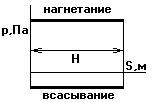
Индикаторная диаграмма насоса
Как правило, из паспорта известен диаметр поршня, по нему можно определить площадь Sп= p.d2/4, тогда сила: F=p.Sп
Правило знаков сил и моментов:
· Сила считается положительной, если она по направлению совпадает с направлением движения того звена, к которому эта сила приложена.
· Момент считается положительным, если его направление совпадает с направлением угловой скорости вращения данного звена.
Имея механическую характеристику поршневой машины и учитывая правило знаков, то можно перестроить в график сил (см. лабораторную работу №4).
Основной вывод:
В течение всего цикла работы поршневой машины сила, приложенная к поршню, будет изменяться как по величине, так и по направлению, это в свою очередь приводит к колебаниям угловой скорости главного вала рабочей машины.
§2.3 Понятие о расчетной схеме машинного агрегата и переход от нее к динамической модели.
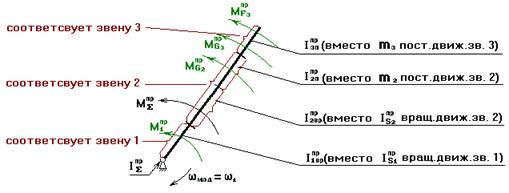
На расчетной схеме машинного агрегата отмечают основные силовые факторы, действующие в машинном агрегате; основные массы звеньев, влияющих на закон движения машинного агрегата; и основные жесткости валов. На рис.5-92 показан переход от реальной схемы к расчетной схеме (а) и от нее к динамической модели.
Из множества масс выделены 3 основные, оказывающие самое большое внимание на закон движения.
Расчетная схема (б) – 3-х массовая динамическая модель.
Для описания закона движения 3-х массовой динамической модели необходимо 3 дифференциальных уравнения.
Если положить жесткость с1 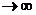 , то можно перейти к двумассовой модели (необходимо 2 диф. уравнения).
, то можно перейти к двумассовой модели (необходимо 2 диф. уравнения).
Если положить жесткость с2 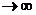 , то получим одномассовую динамическую модель (рис. 2.3).
, то получим одномассовую динамическую модель (рис. 2.3).
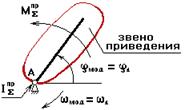
Рис. 2.3
Можно иметь 2 вида одномассовых динамических моделей:
1. Если звено приведения совершает вращательное движение, то одномассовая модель имеет вид
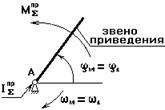
закон движения должен быть один,
поэтому wм = w1 , jм = j1
Уравнение движения можно записать одним уравнением, в виде изменения кинетической энергии:
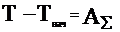
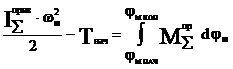
2. 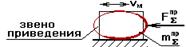 Если звено приведения совершает поступательное движение, то одномассовая модель имеет вид:
Если звено приведения совершает поступательное движение, то одномассовая модель имеет вид:
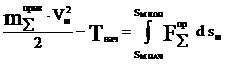
Этот вид рассматривать не будем.
§2.4 Приведение сил и масс к одномассовой динамической модели.
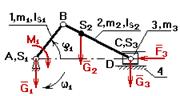 j1 – обобщенная координата.
j1 – обобщенная координата.
Нужно определить закон движения 1-го
звена данного механизма.
Дано: j1, w1, lAB, lBC, lBS2, G2, G3, F3, IS1, IS2.
Определить, как изменяется w1.
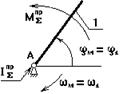 |
При переходе от расчетной схеме к одномассовой механической модели за звено приведения, как правило, принимают то звено, закон движения которого определяют.
Звено приведения – зв.1; изобразим одномассовую модель:
2.4.1 Приведение масс.
При переходе от расчетной схемы к модели необходимо обеспечить равенство кинетической энергии звена приведенной модели и реального механизма:
ТМод = ТМех .
Кинетическая энергия модели должна быть равна кинетической энергии сего механизма.
Тмод = Тпост + Твращ
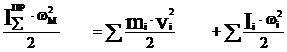
Лекция 4.
 |
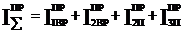
Приведение масс основано на равенстве кинетических энергий реальных звеньев и звена приведения одномассовой модели.
Если требуется определить какую-либо составляющую 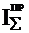 , например
, например 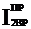 , то записывают равенство:
, то записывают равенство:
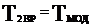
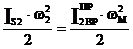
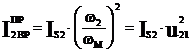
2.4.2 Приведение сил.
АΣ –работа суммарного приведенного момента на его возможное перемещение.
Т – Тнач = АΣ
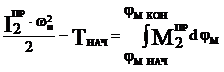
 (1)
(1)
Приведение сил основано на равенстве секундных работ (мощностей) реальных сил и моментов, приложенных к звеньям механизма, на их возможных перемещениях и суммарного приведенного момента, приложенного к звену приведения, на его возможное перемещение.
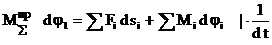
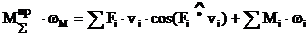
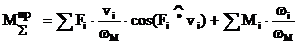
Передат передаточ
Функция отношение
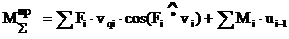
Вместо силы 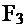 – момент
– момент 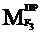 .
.
Если необходимо определить какую-либо составляющую суммарного приведенного момента, например 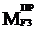 , то необходимо записать равенство:
, то необходимо записать равенство:
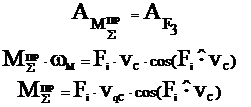
§2.5 Вывод формулы для определения закона движения звена приведения в форме кинетической энергии (определение ωм).
из выражения (1) получаем, что wм равна
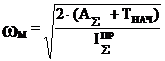
2.5.1 Определение АΣ(графический метод).
Для определения АΣ необходимо построить график 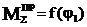 .
.
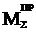 определяется по вышеприведенным зависимостям.
определяется по вышеприведенным зависимостям.
График АΣ строится методом графического интегрирования 
Суть метода: на продолжении оси абсцисс слева выбирается произвольный отрезок интегрирования ОК, чем он длиннее, тем более пологим будет график АΣ . Затем площадь под кривой М(φ1) на каждой итерации заменяется площадью равновеликого прямоугольника.
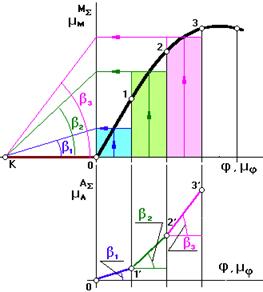
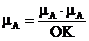
2.5.2 Определение закона движения звена приведения в дифференциальной форме (определение e звена приведения).
Чтобы избавиться от интеграла в (1), продифференцируем (1) по обобщенной координате φм, получим
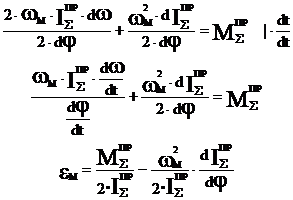
(3)
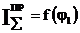 2.5.3 Определение
2.5.3 Определение 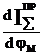 графическим методом .
графическим методом .
Строим график .
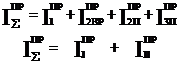
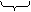
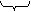
Const var
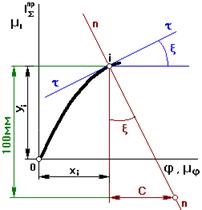
В соответствии с определением производной проведем касательную к кривой в точке i и определим тангенс угла наклона этой касательной. Для этого проведем нормаль через точку i. Тогда
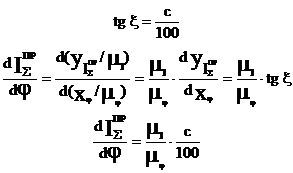
2.5.4 Определение eмодели по известному графику wм=f(φ1).
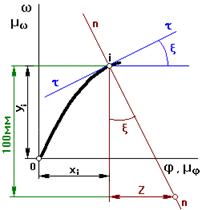
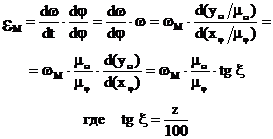
§2.6 Режимы работы машинного агрегата.
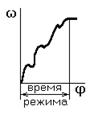
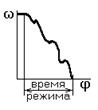
а) разгон б) торможение (выбег)
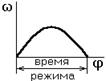 | 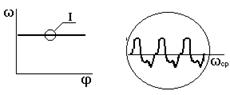 | ||
в) безударный останов г)
рис. 2.6
а),б),в) – неустановившийся режим;
г) – установившийся режим.
2.6.1 Определение законов движения звена приведения одномассовой динамической модели при неустановившемся режиме работы машинного агрегата.
Угловая скорость определяется по (2).
Угловое ускорение определяется по (3).
Время режима определяется по формуле:
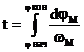
2.6.2 Определение законов движения для установившегося режима работы .
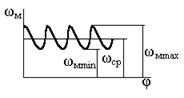
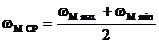
Отклонения угловой скорости от среднего уровня характеризуется коэффициентом неравномерности d
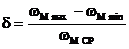
Коэффициент d определяется экспериментально и для различных машин имеет значения:
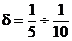 машины ударного действия (прессы, молоты)
машины ударного действия (прессы, молоты)
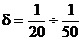 полиграфические машины (насосы)
полиграфические машины (насосы)
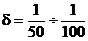 электрогенераторы переменного тока
электрогенераторы переменного тока
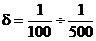 электрогенераторы постоянного тока
электрогенераторы постоянного тока
ЛЕКЦИЯ 5.
Для определения угловой скорости
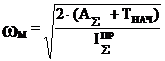 ,
,
где 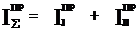
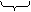
Const var
Для того чтобы удерживать колебания угловой скорости wм в заданных пределах, определяемых коэффициентом неравномерности d, первая группа звеньев должна иметь 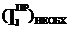
2.6.3 Вывод формулы для определения 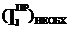 .
.
Изменение wм от wм_max до wм_min приводит к изменению кинетической энергии первой группы звеньев (ΔТI), которое равно:
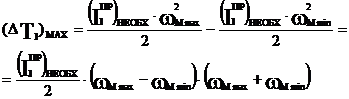
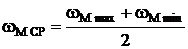
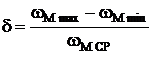
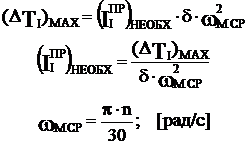 (2)
(2)
При установившемся режиме работы при определении wм формулу (1) напрямую использовать нельзя, т.к. неизвестно Тнач, поэтому задачу решают, используя метод Мерцалова (см. учебник).
§2.7 Определение реакций в кинематических парах рычажных механизмов без учета трения.
Данная задача может быть решена:
1. аналитическим способом;
2. графическим способом (см.ДЗ №2).
Аналитический способ:
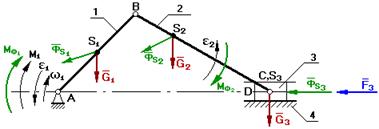 Изобразим схему кривошипно-ползунного механизма.
Изобразим схему кривошипно-ползунного механизма.
Дано:
F3, G1, ФS1, MФ1, G2,
ФS2, МФ2, G3, ФS3,
wi, ei, vi, ai.
Определить:
М1 и Qij
Задачу начинают решать с того звена, к которому приложена известная сила или момент. Кроме того, введем понятие входной шарнир (проекции реакции Q на оси х и у положительны) и выходной шарнир (проекции реакции Q на оси - отрицательны).
Расстояние от входного шарнира до центра масс звена – р, а расстояние от выходного шарнира до центра масс звена – q.
Звено 1
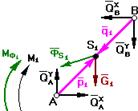
Шарнир А - входной
Шарнир В - выходной
Звено 2
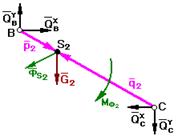
Шарнир В - входной
Шарнир С - выходной
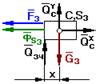 |
Звено 3
При решении задачи используется принцип Даламбера
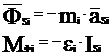
3 звено:
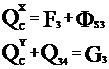
2 звено:
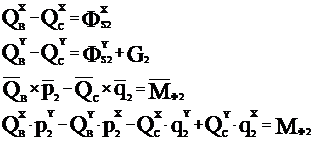
1 звено:
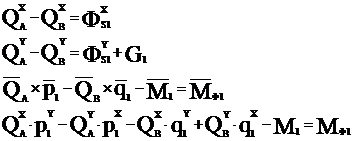
Составим систему уравнений в матричной форме:
| неизвестные | QAx | QAy | QBx | QBy | QCx | QCy | Q34 | M1 | ||||||
| F3+ФS3 | = | х | QAx | |||||||||||
| G3 | QAy | |||||||||||||
| ФS2x | -1 | QBx | ||||||||||||
| ФS2y+G2 | -1 | QBy | ||||||||||||
| MФ2 | p2y | -p2x | -q2y | q2x | QCx | |||||||||
| ФS1x | -1 | QCy | ||||||||||||
| ФS2y+G2 | -1 | Q34 | ||||||||||||
| MФ1 | p1y | -p1x | -q1y | q1x | -1 | M1 | ||||||||
B A x
Эта система решается методом Гаусса.
§2.8 Учет трения при определении реакций в кинематических парах.
Трение является сложным физико-химическим процессом, сопровождающийся выделением тепла. Это вызвано тем, что перемещающиеся тела оказывают сопротивление относительному движению. Мерой интенсивности сопротивления относительному перемещению является сила (момент) трения.
Различают трение качения, трение скольжения, а также сухое, граничное и жидкостное трение.
Если суммарная высота микронеровностей взаимодействующих поверхностей:
· больше, чем высота слоя смазки, то - сухое трение.
· равна высоте слоя смазки, то -граничноетрение.
· меньше, чем высота слоя смазки, то - жидкостное .
2.8.1 Учет трения в поступательной кинематической паре.
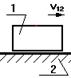 Без учета трения реакция направлена по нормали к взаимодействующим поверхностям. При учете трения результирующая реакция Q21 отклоняется от общей нормали на угол трения j в сторону противоположную направлению движения.
Без учета трения реакция направлена по нормали к взаимодействующим поверхностям. При учете трения результирующая реакция Q21 отклоняется от общей нормали на угол трения j в сторону противоположную направлению движения.
без учета трения с учетом трения
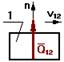
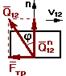 Fтр=Qn12.tg j
Fтр=Qn12.tg j
tg j= f
Fтр=Qn12.f
Коэффициент трения f определяется экспериментально и зависит от многих факторов.
2.8.2 Учет трения во вращательной кинематической паре.
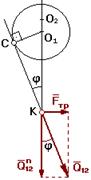
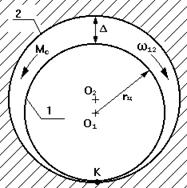
1 - цапфа
rц - радиус цапфы
Δ - зазор
r - радус круга трения;
r = О1С
Из ΔО1СК à 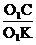 = sin j à О1С = О1К sin j
= sin j à О1С = О1К sin j
Mc= Q12.О1С = Q12. rц.sin j
При малых углах j sin j ≈ tg j = f . Тогда :
Mc= Q12. rц.f
При учете трения во вращательной КП результирующая реакция отклоняется от общей нормали на угол трения j и проходит касательно к кругу трения радиуса r
ЛЕКЦИЯ 6.
2.8.3 Краткие сведения по определению КПД (h) машинного агрегата.
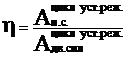 КПД машинного агрегата равен отношению работы сил полезного сопротивления к работе движущих сил за цикл установившегося режима.
КПД машинного агрегата равен отношению работы сил полезного сопротивления к работе движущих сил за цикл установившегося режима.
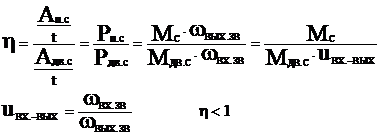
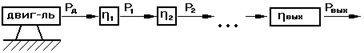 |
а) определение КПД при последовательном соединении механизмов.
Pвход = Рд
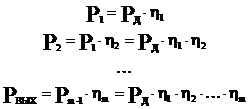
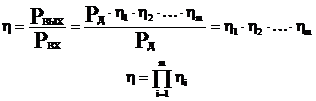
б) определение КПД при параллельном соединении механизмов.
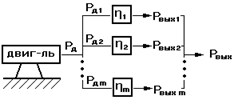 |
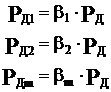
где bi – коэффициенты распределения мощности.
b1 + b2 + b3 +… + bm = 1
Каждый b определяется назначением специалиста.
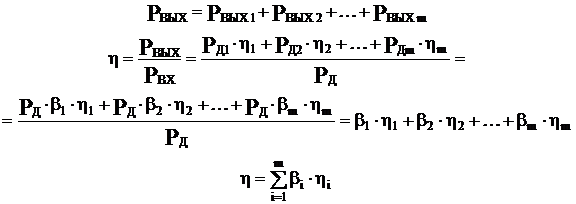
Глава3. Основные сведения о виброзащите машинного агрегата.
Вибрации нашли полезные применения в технике. Примерами этого являются различные вибромассажеры, вибротранспортеры и т.д. Однако работа с инструментом, основанном на вибрации, приводит к профессиональным травмам и заболеваниям. Основные мероприятия, связанные с выявлением источника вибрации, с целью последующего снижения его виброактивности или полного его устранения, называют виброзащитой.
Виброзащита осуществляется по следующим основным направлениям:
1. Уменьшение активности источника с помощью статического уравновешивания механизмов (полного или частичного), а также уравновешивания роторов.
2. Изменение конструкции объекта: установка гасителей колебаний, демпферов, виброизоляторов.
§3.1 Статическое уравновешивание рычажных механизмов.
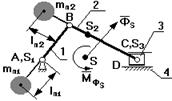 Если
Если 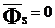 , то такой механизм называется статически уравновешенным.
, то такой механизм называется статически уравновешенным.
Если 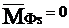 , то такой механизм называется моментно-уравновешенным.
, то такой механизм называется моментно-уравновешенным.
Рассмотрим случай, когда необходимо уравновесить статически,
т.е. 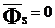 . Этого можно добиться только тогда, когда
. Этого можно добиться только тогда, когда 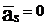 , т.к.
, т.к.
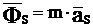 S à A
S à A
Когда центр масс совмещен с А, то он становиться неподвижным. Этого добиваются с помощью двух противовесов, один из которых устанавливается на продолжении шатуна, а другой на продолжении кривошипа.
Для того чтобы рассчитать массы противовесов, применяют метод замещающих масс, суть которого заключается в том, что масса каждого звена условно разноситься по двум точкам. При этом должны выполняться следующие условия:
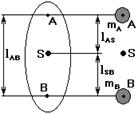 разнесем массу этого звена по точкам А и В так, чтобы положение центра масс не изменилось.
разнесем массу этого звена по точкам А и В так, чтобы положение центра масс не изменилось.
m = mA + mB
lAB = lAS + lBS
mA lAS = mB lBS
Сосредоточим массу 3-го звена в т.С
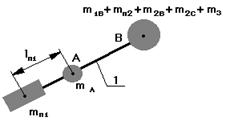
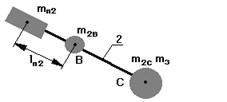 Массу 2-го звена разнесем по шарнирам В и С. Если на продолжении звена 2 поставить противовес массой mпр2 и на расстоянии от т.В равное lпр2, то центр масс звеньев 2 и 3 переместиться в т.В, при этом
Массу 2-го звена разнесем по шарнирам В и С. Если на продолжении звена 2 поставить противовес массой mпр2 и на расстоянии от т.В равное lпр2, то центр масс звеньев 2 и 3 переместиться в т.В, при этом
mпр2.lпр2 = (m2C + m3C).lBC
При этом либо задаются массой противовеса и определяют lпр2, либо задаются lпр2 и определяют массу противовеса.
mпр1.lпр1 = (m1B + mпр2+ m2В+ m2C+ m3C).lAB
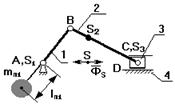 |
После всех указанных мероприятий, центр масс переместиться в точку А, однако невсегда конструктивно возможно установить противовес на продолжении шатуна и ограничиваются установкой противовеса на звене 1. В этом случае центр масс системы смещают на линию АС, и этот центр масс перемещается с постоянным ускорением: а = const
В этом случае механизм – частично статически уравновешанный, его нежелательно устанавливать на высоком фундаменте, т.к. главный вектор сил инерции создает опрокидывающий момент, что недопустимо.
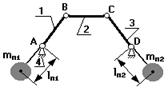 В четырехшарнирном механизме центр масс системы разноситься по точкам А и D, а противовесы устанавливаются на продолжении звеньев 1 и 3.
В четырехшарнирном механизме центр масс системы разноситься по точкам А и D, а противовесы устанавливаются на продолжении звеньев 1 и 3.
§3.2 Балансировка ротора (лаб. раб. №9).
Ротор – тело любой геометрической формы, имеющее свое основное движение – движение вращения (коленвал, колесо турбины и т.д.).
Пусть в силу как
