Нахождение законов распределения двумерных случайных величин

Задача 2.6.1

Найти условный закон распределения случайной величины Х, при условии Y=4, если закон распределения двумерной дискретной случайной величины представлен таблицей 11. Являются ли величины Х и Y независимыми?

Таблица 11 – Закон распределения случайной величины (Х,Y)

уj xi
0,1	0,2	0,1	0,1
0,2	0,1	0,2	0,15
0,3			0,05	0,1

Решение:

Найдём безусловные законы распределения случайных величин Х и Y. Для этого, дополним таблицу 11 столбцом и строкой, в которой будем находить суммы вероятностей соответственно в строках и в столбцах (см. таблицу 5). Получим таблицу 12.

Таблица 12 – Отыскание безусловных вероятностей случайных величин Х и Y по данным задачи 2.6.1

уj xi					Вероятности значений Х
0,1	0,2	0,1	0,1		0,40
0,2	0,1	0,2	0,15		0,45
0,3			0,05	0,1	0,15
Вероятности значений Y	0,3	0,3	0,3	0,1

Безусловные законы распределения случайных величин Х и Y оформим в виде таблиц (таблицы 13 и 14 соответственно).

Таблица 13 – Безусловный закон распределения случайной величины Х

(в задаче 2.6.1)

Х	0,1	0,2	0,3
Р(Х)	0,40	0,45	0,15

Таблица 14 – Безусловный закон распределения случайной величины Y

(в задаче 2.6.1)

Y
Р(Y)	0,3	0,3	0,3	0,1

Используя обозначения таблиц 5 и 6, а также формулу (39), найдём :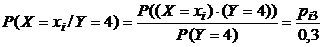

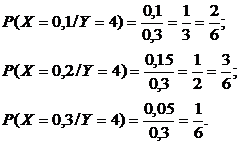
При этом выполняется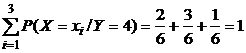

Условный закон распределения случайной величины Х, при условии Y = 4, можно представить таблицей 15.

Таблица 15 – Закон распределения случайной величины Х/(Y = 4) к задаче 2.6.1

Х	0,1	0,2	0,3

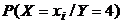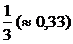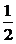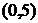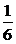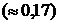Сравним вероятности значений случайной величины X в условном (табл. 15) и безусловном (табл. 13) законах распределения. Если бы величины Х и Y были независимы, распределение величины X не зависело бы от условий, а вероятности в обоих законах были бы одними и теми же.

Таким образом, сравнивая законы, можно сделать вывод о наличии зависимости между величинами Х и Y.

Замечание: в случае, если условный закон распределения Х при некотором условии совпадёт с её безусловным законом распределения, вывод о независимости величин Х и Y сделать будет нельзя: потребуется проверка всех остальных условий.

Ответ: условный закон распределения случайной величины Х, при условии Y=4, представлен в таблице 15; величины Х и Y зависимы.

Задача 2.6.2

Найти плотности распределения величин Х и Y, если известна их совместная плотность распределения (плотность распределения двумерной случайной величины (Х и Y)):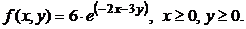

Решение:

Используя формулы (41) и (42), а также с учётом условий: 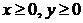, получим:

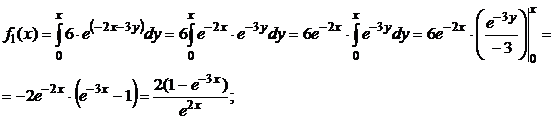
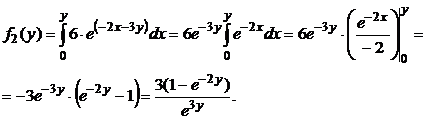
Ответ: плотности распределения величин Х и Y соответственно равны 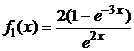и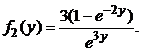

ОБЩИЕ ПРАВИЛА ОФОРМЛЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ

Контрольная работа оформляется согласно Стандарту организации СТО 01.04 – 2005: «Работы студентов. Общие требования и правила оформления», выполняется на листах формата А4 и состоит из титульного листа, задания, листа для замечаний и основной части.

Титульный лист оформляется на специальном бланке, форма которого выдаётся кафедрой прикладной математики вместе с заданием. Основная часть содержит решение задач, при необходимости рисунки со схемами или графиками, поясняющими решение.