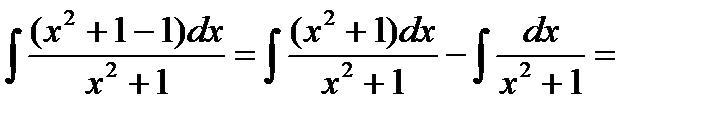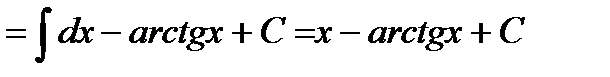Правило нахождения точек перегиба

графика функции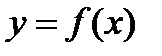

1.Найти вторую производную .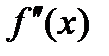

2.Найти критические точки II рода функции 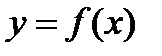, т.е. точки, в которой 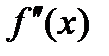обращается в нуль или терпит разрыв.

3.Исследовать знак второй производной 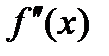впромежутка, на которые найденные критические точки делят область определения функции 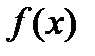. Если при этом критическая точка 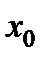разделяет промежутки выпуклости противоположных направлений, то 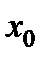является абсциссой точки перегиба графика функции.

4.Вычислить значения функции в точках перегиба.

Пример 1: Найти промежутки выпуклости и точки перегиба следующей кривой: .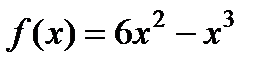

Решение: Находим , .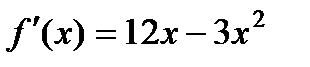

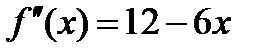Найдем критические точки по второй производной, решив уравнение .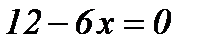

.

	+		-
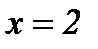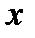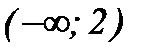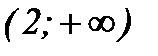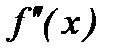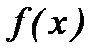		точка перегиба

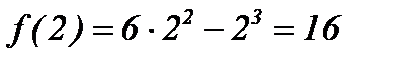
Ответ: Функция выпукла вверх при ;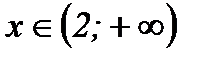

функция выпукла вниз при ;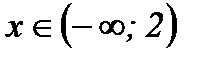

точка перегиба .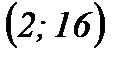

Общая схема для построения графиков функций

1. Найти область определения функции .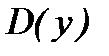

2. Найти точки пересечения графика функций с осями координат.

3. Исследовать функцию на четность или нечетность.

4. Исследовать функцию на периодичность.

5. Найти промежутки монотонности и точки экстремума функции.

6. Найти промежутки выпуклости и точки перегиба функции.

7. Найти асимптоты функции.

8. По результатам исследования построить график.

Пример: Исследовать функцию и построить ее график:

.

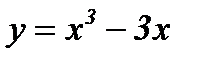Решение:

1) Функция определена на всей числовой оси, т. е. ее область определения .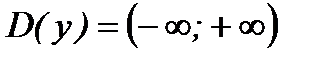

2) Найдем точки пересечения с осями координат:

с осью ОХ : решим уравнение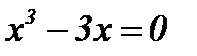

.

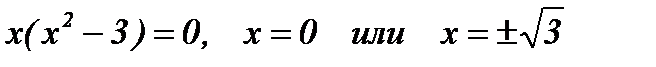с осью ОY: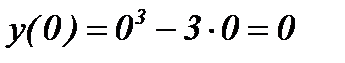

3) Выясним, не является ли функция четной или нечет

ной:

.

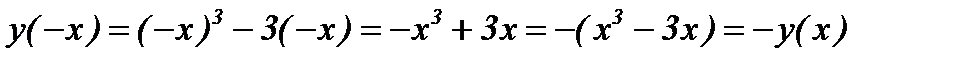Отсюда следует, что функция является нечетной.

4) Функция непериодична.

5) Найдем промежутки монотонности и точки экстремума функции: .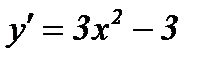

Критические точки: .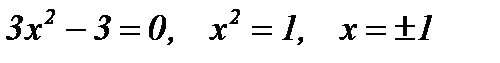

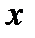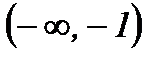		-1		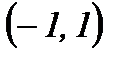1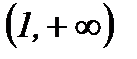
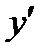	+	0	-	0	+
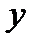		т. max		т. min -2

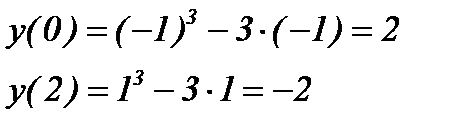
6) Найдем промежутки выпуклости и точки перегиба функции: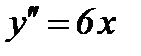

Критические точки: .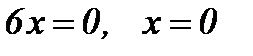

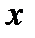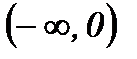		0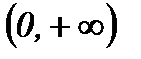
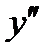	-	0	+
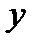		точка перегиба

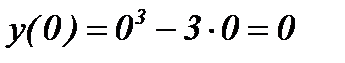
7) Функция непрерывна, асимптот у нее нет.

8) По результатам исследования построим график функции:

y

1 x

-2

Интегральное исчисление

Неопределенный интеграл. Методы вычисления

Определение:Функция F(x) называется первообразнойдля функции f(x), ес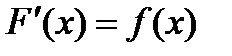ли или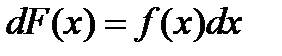

Любая непрерывная функция f(x) имеет бесконечное множество первообразных, которые отличаются друг от друга постоянным слагаемым.

Определение: Совокупность F(x)+С всех первообразных для функции f(x) называется неопределенным интегралом от этой функции и обозначается:

.

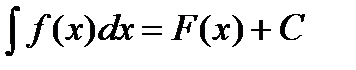Основные свойства неопределенного интеграла:

1.

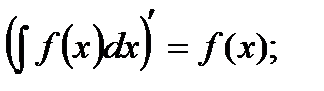
2. ;

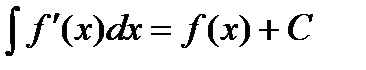3.

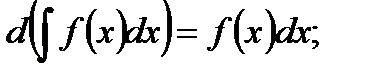
4. ;

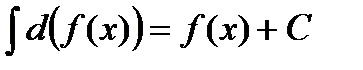5. ;

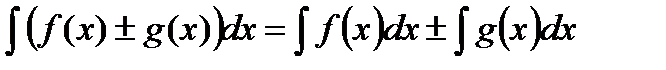6. .

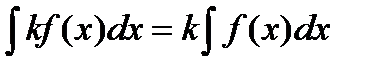Непосредственное интегрирование

Непосредственное интегрирование предполагает использование при нахождении неопределенных интегралов таблицы интегралов

Таблица интегралов

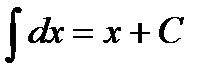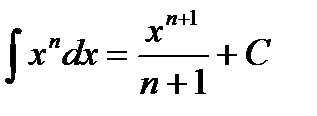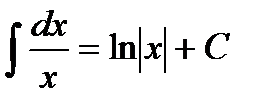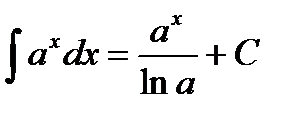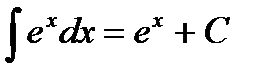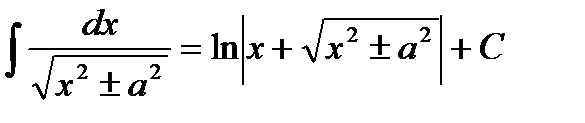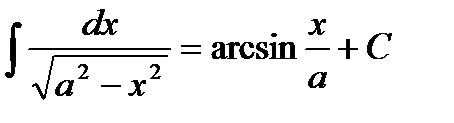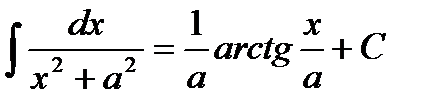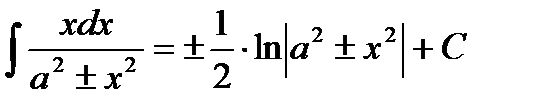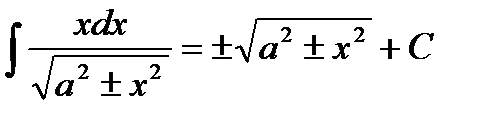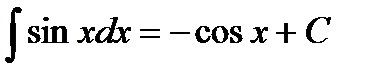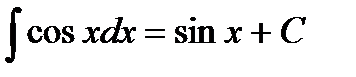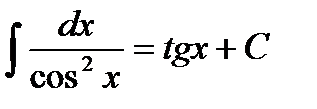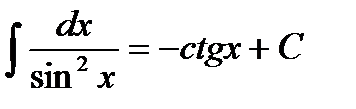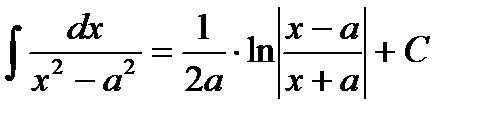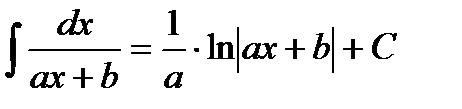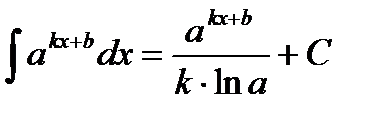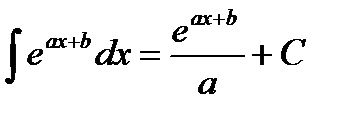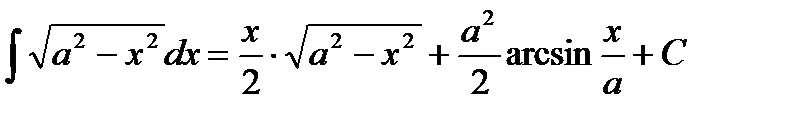
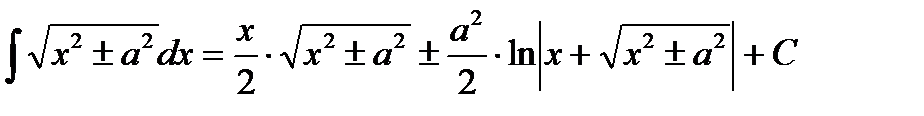
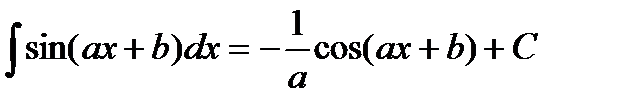
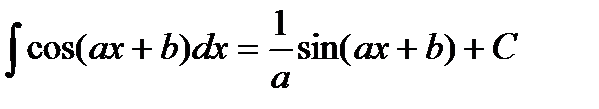
Рассмотрим нахождение интегралов непосредственным методом.

Пример 1: Найти неопределенный интеграл:

.

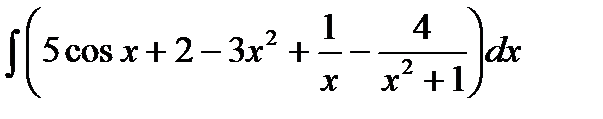Решение: =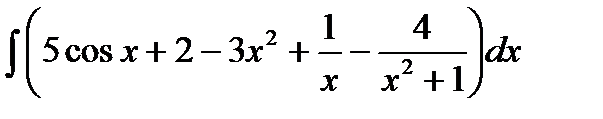

=

.

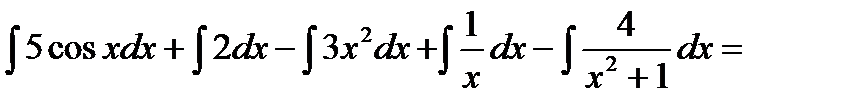
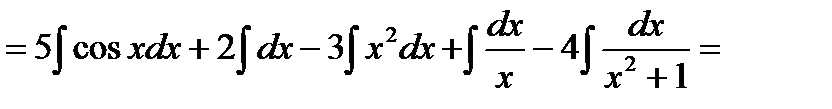
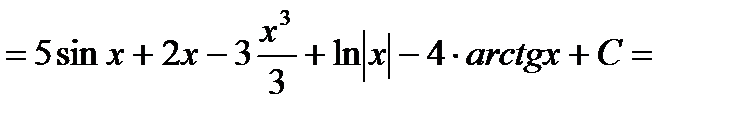
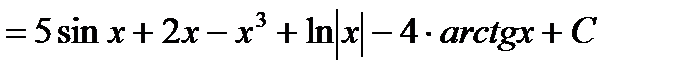Пример 2: Найти неопределенный интеграл: .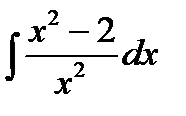

Решение: =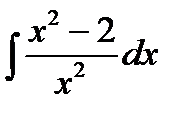

.

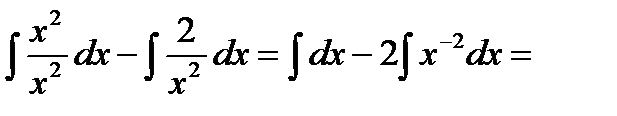
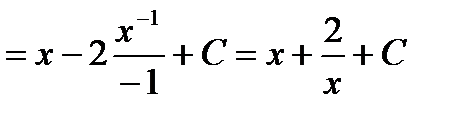Пример 3: Найти неопределенный интеграл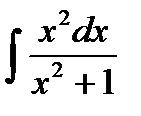

Решение: 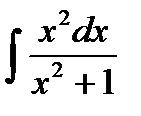=