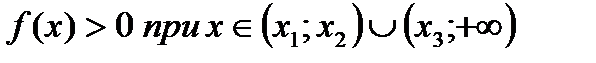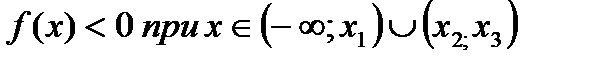Раздел VII. Аналитическая геометрия
МАТЕМАТИКА
Методическое пособие
для студентов заочной формы обучения
по специальностям 35.02.03 «Технология деревообработки», 35.02.02 «Технология лесозаготовок»
Комсомольск-на-Амуре
Составитель:Ангерт Марина Валерьевна - преподаватель математики
Рецензенты:
Методическое пособие предназначено для студентов – заочников, обучающихся по специальностям 35.02.02, 35.02.03
В пособии по каждой теме дисциплины содержится краткий теоретический материал, образцы решения и оформления примеров, литература, необходимая при изучении материала, а также вопросы для самопроверки.
Приведены задания обязательной контрольной работы по дисциплине «Математика».
Введение
Курс математики, который предстоит освоить студенту – заочнику, является фундаментом математического образования. Математические знания важны для успешного изучения общетеоретических и специальных дисциплин, которые предусмотрены учебными планами различных специальностей.
По специальностям 35.02.02, 35.02.03 математика изучается в течение одного семестра. По результатам изучения дисциплины студенты должны выполнить одну контрольную работу и сдать дифференцированный зачёт. В межсессионный период и во время сессий со студентами – заочниками проводятся лекционные и практические занятия, а также консультации.
В настоящем пособии содержатся общие рекомендации студентам – заочникам по работе над курсом математики, программа курса, методические указания по темам дисциплины с вопросами для самопроверки, решения типовых задач и задания контрольных работ.
Общие рекомендации по работе
над курсом математики
Формой обучения студента – заочника является самостоятельная работа над учебным материалом, которая состоит их следующих элементов: изучение материала по учебникам, решение задач, самопроверка, выполнение контрольных работ. В процессе самостоятельной работы студент может обращаться к преподавателю с вопросами для получения письменной или устной консультации. В помощь заочникам организуются чтение лекций, практические занятия. Завершающим этапом изучения курса математики является сдача семестрового дифференциального зачёта в соответствии с учебным планом по специальности.
Изучение материала по учебнику
Изучение материала по учебнику следует выполнять согласно указанным в программе курса темам. Изучая тот или иной вопрос темы по учебнику, целесообразно выполнять на бумаге все вычисления и вычерчивать имеющиеся в учебнике чертежи.
При самостоятельном изучении материала полезно вести конспект. В конспект по мере проработки материала рекомендуется вписывать определения, теоремы, формулы, уравнения и т.п. Поля конспектов могут послужить для выделения тех вопросов, на которые необходимо получить письменную или устную консультации. Ведение конспекта должно быть аккуратным, расположение текста хорошо продуманным. Конспект поможет в подготовке к теоретической части экзамена.
Решение задач
Чтение учебника должно сопровождаться разбором предлагаемых решений задач.
Каждый этап решения задачи должен быть обоснован, исходя из теоретических положений курса. Решение задач и примеров следует излагать подробно, вычисления располагать в строгом порядке, отделяя вспомогательные вычисления от основных. Чертежи можно выполнять от руки, но аккуратно.
В промежуточные вычисления не следует вводить приближенные значения корней, числа p и других математических констант.
Самопроверка
Опыт прочного усвоения материала темы показывает, что самопроверку проводить необходимо. В настоящем пособии приводятся для самопроверки вопросы, которые акцентируют внимание на наиболее важных, ключевых положениях темы. В процессе выполнения самопроверки необходимо избегать пользования учебником или конспектом. Желание обратиться к учебнику или конспекту показывает недостаточное усвоение материала темы.
Консультации
При изучении теоретического материала или при решении задач у студента могут возникнуть вопросы, разрешить которые самостоятельно не удается. В такой ситуации студенту следует обратиться к преподавателю для получения от него письменной или устной консультации. При этом необходимо точно указать вопрос, учебник и место в учебнике, где рассмотрен затрудняющий студента вопрос. Если непреодолимые затруднения возникли при решении задачи, то следует указать характер затруднения, привести план решения.
Контрольная работа
В процессе изучения курса студент должен выполнить одну контрольную работу, которая проходит рецензирование. По полученным результатам студент может сделать выводы о степени усвоения им соответствующего раздела курса, внести коррективы в процесс последующей самостоятельной работы по изучению теоретического материала.
К выполнению контрольной работы следует приступать после тщательного разбора имеющихся в учебнике и сборниках задач решений с ответами. В дополнение к предложенным задачам сборников в данном пособии рассмотрены некоторые примеры.
Контрольные работы должны выполняться самостоятельно, так как в противном случае рецензирование работы как диалог общения преподавателя – рецензента и студента с целью оказания последнему методической помощи не достигнет цели.
Прорецензированные и зачтенные контрольные работы вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, следует сохранять, поскольку без их предъявления студент не допускается к сдаче экзамена.
Лекции, практические занятия
Во время экзаменационных сессий для студентов - заочников читаются лекции, проводятся занятия. На лекциях и практических занятиях проводится обзор наиболее важных разделов курса, могут рассматриваться отдельные вопросы программы, отсутствующие или недостаточно полно освященные в рекомендуемых учебных пособиях.
Зачеты
К зачету допускаются студенты, выполнившие контрольную работу (работы должны быть зачтены преподавателем-рецензентом).
Учебный план по дисциплине «МАТЕМАТИКА»
| Специальность | Семестр | Диф.зачет | Контрольная работа | Часы учебных занятий | |||
| Всего | Само-стояте-льная работа | Лек-ции и прак-тика | Кон-суль-тации | ||||
| 35.02.02 | |||||||
| 35.02.03 |
Программа дисциплины«МАТЕМАТИКА»
Раздел I. Элементы линейной алгебры
Тема 1: Матрицы и определители
Понятие матрицы. Квадратная и транспонированная матрица. Перестановки. Действия над матрицами. Ранг матрицы. Определители и их свойства. Правило Крамера.
Тема 2. Системы линейных уравнений
Понятие системы линейных уравнений. Формулы Крамера. Матричное решение систем линейных уравнений. Метод Гаусса. Теорема Кронекера-Капелли.
Раздел II. Введение в математическийанализ
Тема 1: Переменные величины и функции
Определение функции. Классификация функций. Область определения и область значения функций. Свойства функций: нули функции, четность, нечетность, периодичность, монотонность, точки локального экстремума, промежутки знакопостоянства.
Тема 2. Теория пределов
Предел функции в точке и на бесконечности. Основные теоремы о пределах: предел суммы и разности двух функций, предел произведения двух функций, предел отношения двух функций. Техника вычисления пределов.
Раздел III. Дифференциальное исчисление
Тема 3. Производная и дифференциал функции
Определение производной. Геометрический и механический смысл производной. Правила дифференцирования функции. Таблица производных. Производные от сложных функций. Дифференциал. Производные высших порядков.
Тема 4. Применение производной к исследованию функций
Условия возрастания и убывания функции. Точки экстремума функции. Выпуклость, вогнутость кривой, точки перегиба. Общая схема исследования функции и построения ее графика.
Раздел IV. Интегральное исчисление
Тема 5. Неопределенный интеграл
Понятие первообразной. Свойства неопределенных интегралов. Таблица интегралов. Основные методы интегрирования: непосредственный метод, метод подстановки.
Тема 6: Определенный интеграл
Определение определенного интеграла, его геометрический смысл. Свойства определенного интеграла. Формула Ньютона – Лейбница. Основные методы вычисления определенного интеграла: непосредственный метод, метод замены переменных.
Раздел V. Дифференциальные уравнения
Тема 7. Дифференциальные уравнения первого порядка
Дифференциальные уравнения первого порядка. Общее решение. Частное решение. Понятие о задаче Коши. Дифференциальные уравнения первого порядка с разделяющимися переменными. Однородные дифференциальные уравнения первого порядка. Линейные дифференциальные уравнения первого порядка.
Раздел VI. Числовые и функциональные ряды
Тема 8. Теория рядов
Числовой ряд. Ряд Тейлора, ряд Маклорена. Нахождение значений Функци с помощью ряда Маклорена.
Литература
Основная
1. Валуцэ И.И., Дилигул Г.Д. Математика для техникумов на базе средней школы: Учебное пособие, М.: Наука. Гл. ред. физ. мат. литературы, 1990
2. Алгебра и начала анализа/ под редакцией Г.Н.Яковлева, М.: Наука: Наука. Гл. ред. физ. мат. литературы, 1981. – Ч.1,2.
3. Богомолов В.Н. Практические занятия по математике, М.: Высшая школа, 1982.
4. Шипачев В.С. Высшая математика, М.: Высшая школа, 1990.
5. Шипачев В.С. Задачник по высшей математике, М.: Высшая школа, 1998
6. Пехлецкий И.Д. Математика, СПО. – М.: Академия, 2008.
7. Григорьев С.Г., Задулина С.В. Математика, СПО. – М.: Академия,2009.
8. Спирина М.С., Спирин П.А. Теория вероятностей и математическаястатистика, СПО. – М.: Академия, 2007.
9. Валуце И.И., Дилигул Г.Д. Математика для техникумов. – М.: Наука,1980.
10. Башмаков М.И. Математика, 10 кл. – М.: Академия, 2009.
11. Башмаков М.И. Математика, 11 кл. – М.: Академия, 2009.
Дополнительная
12. Справочник по математике, М.: «Лист»,1999.
13. Кудрявцев Л.Д. Краткий курс математического анализа. М.: Наука. Гл. ред. физ. мат. литературы, 1989.
14. Шибасов Л.П., Шибасова З.Ф. За страницами учебника математики. – М.: Просвещение, 1997.
Методические указания
Матрицы и определители
Виды матриц.
Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера п × п называют матрицей п-го порядка.
Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.
Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой E.
Например  − единичная матрица 3-го порядка.
− единичная матрица 3-го порядка.
Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.
Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой О.
Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка соответственно). Их вид:
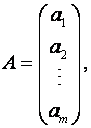 B=(b1 b2… bn)
B=(b1 b2… bn)
Матрица, полученная из данной заменой каждой её строки столбцом с тем же номером, называется матрицей,транспонированной к данной. Обозначается AT.
Так, если A= 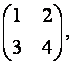 то AT=
то AT= 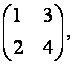 если A=
если A= 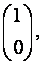 то AT= (1 0)
то AT= (1 0)
Транспонированная матрица обладает следующим свойством: (AT)T=A.
Операции над матрицами
Умножение матрицы на число.
Произведением матрицы Amn=(aij) начисло kназывается матрица Bmn=(bij) такая, что (bij)=k· aij 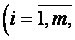
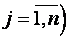
2. Сложение матриц.
Операция сложения матриц вводится только для матриц одинаковых размеров.
Суммой двух матриц Amn=(aij) и Bmn=(bij) называется матрица Cmn=(cij)такая, что cij= aij+ bij 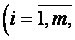
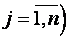 .
.
Пример.
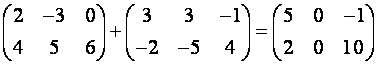 .
.
3. Вычитание матриц.
Разность матриц А – В можно определить так: А – В = А + (–В).
Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:
1. А + В = В + А;
2. А + (В + С) = (А + В) + С;
3. А + О = А;
4. А – А = О;
5. 1 · А = А;
6. α ·(А + В) = αА + αВ;
7. (α+ β) ·А = αА + βА;
8. α·(βА) = (αβ) ·А,
где А, В, С – матрицы, α и β – числа.
Элементарные преобразования матриц
Элементарными преобразованиями матриц являются:
• перестановка местами двух параллельных рядов матрицы;
• умножение всех элементов ряда матрицы на число, отличное от нуля;
• прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.
Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается А~В.
При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю. Такую матрицу называют канонической, например
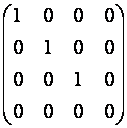
4. Произведение матриц.
Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.
Произведением матрицы на матрицу Amn=(aij) и Bnp=(bjk) называется матрица Cmp=(cik) такая, что
cik=ai1∙b1k+ai2∙b2k+…+ ain∙bnk, где 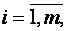
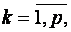
т. е. элемент i-й строки и k-го столбца матрицы произведения С равна суммы произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца матрицы В.
Получение элементаcikсхематично изображается так:
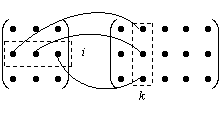
Если матрицы AиВ квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А·Е = Е·А = А, где А − квадратная матрица, Е − единичная матрица того же размера.
Пример
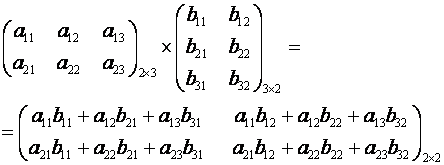
Пример A= 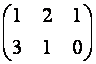 , B=
, B= 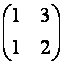 . Тогда произведение А·В не определено, так как число столбцов матрицы А (3) не совпадает с числом строк матрицы В (2). При этом определено произведение В×А, которое считают следующим образом:
. Тогда произведение А·В не определено, так как число столбцов матрицы А (3) не совпадает с числом строк матрицы В (2). При этом определено произведение В×А, которое считают следующим образом:
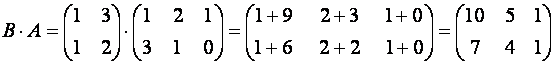
Матрицы А и В называются перестановочными, если АВ = ВА. Умножение матриц обладает следующими свойствами:
1. А·(В·С) = (А·В)·С;
2. А·(В+С) = АВ+АС;
3. (А+В)·С = АС+ВС;
4. α(АВ) = (αА)В,
если, конечно, написанные суммы и произведения матриц имеют смысл.
Для операции транспонирования верны свойства:
1. (А+В)T= АT+ВT;
2. (АВ)T= ВT·АT.
Понятие определителя
Определителем матрицы первого порядкаA=(a11), или определителем первого порядка, называется элемент a11:
Δ1=|A|=a11.
Определителем матрицы второго порядкаA=(aij), или определителем второго порядка, называется число, которое вычисляется по формуле:
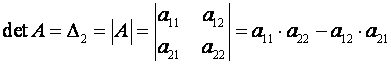
Определитель матрицы A также называют её детерминантом.
Пример Вычислить определитель матрицы.
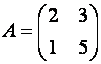
Решение.
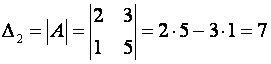
Пример Вычислить определитель матрицы
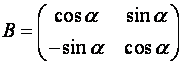
Решение.
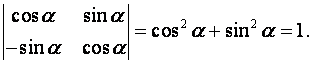
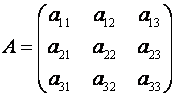
Пусть дана квадратная матрица третьего порядка:
 .
.
Определителем матрицы третьего порядка A=(aij), или определителем третьего порядка, называется число, которое вычисляется по формуле:
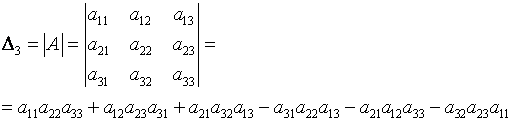
При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса), которое символически можно записать так:

Пример Вычислитьопределитель матрицы
A= 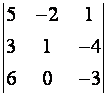 .
.
Решение.
Δ=5∙1∙(-3)+(-2) ∙(-4) ∙6+3∙0∙1-6∙1∙1-3∙(-2) ∙(-3)-0∙(-4) ∙5=-15+48-6-18=9
Для того чтобы ввести понятие определителя более высокого порядка, потребуются некоторые дополнительные понятия.
Свойства определителей
1. Если какой-либо ряд матрицы состоит из одних нулей, то ее определитель равен 0.
2. Если все элементы какого-либо ряда матрицы умножить на число, отличное от нуля, то ее определитель умножится на это число.
3. При транспонировании матрицы ее определитель не изменяется.
4.При перестановке двух параллельных рядов матрицы ее определитель меняет знак на противоположный.
5.Если квадратная матрица содержит два одинаковых ряда, то ее определитель равен 0.
6. Если все элементы некоторого ряда матрицы пропорциональны соответствующим элементам параллельного ряда, то ее определитель равен 0.
7. Сумма произведений элементов какого-либо ряда матрицы на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
8. Определитель матрицы не изменится, если к элементам какого-либо ряда прибавить соответствующие элементы параллельного ряда, предварительно умноженные на одно и то же число.
9. Если элементы какого-либо ряда матрицы представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму соответствующих определителей.
10. Определитель произведения двух квадратных матриц равен произведению их определителей: |C|=|A|·|B|, где C=A·B, А и В − матрицы n-го порядка.
Системы линейных уравнений
Основные понятия и определения
Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных, называется система вида
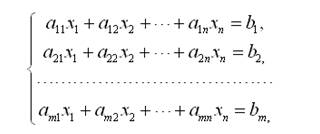
где числа aij, 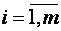 ,
, 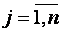 называются коэффициентами системы, числа bi– свободными членами. Подлежат нахождению числа xn.
называются коэффициентами системы, числа bi– свободными членами. Подлежат нахождению числа xn.
Такую систему удобно записывать в компактной матричной форме А·X=B.
Здесь А – матрица коэффициентов системы, называемая основной матрицей:
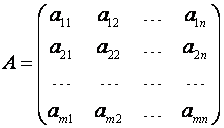 ,
,
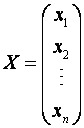 – вектор–столбец из неизвестных xj,
– вектор–столбец из неизвестных xj,
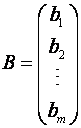 – вектор–столбец из свободных членов bi.
– вектор–столбец из свободных членов bi.
Если к основной матрице A добавить столбец свободных членов, получим расширенную матрицу 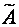
 .
.
Решением системы называется п значений неизвестных x1=c1, x2=c2, …, xn=cn, при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы – столбца 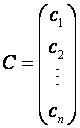 .
.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения.
Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения. В последнем случае каждое ее решение называется частным решением системы. Совокупность всех частных решений называется общим решением.
Решить систему – это значит выяснить, совместна она или несовместна. Если система совместна, найти её общее решение.
Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой, и наоборот.
Эквивалентные системы получаются, в частности, при элементарных преобразованиях системы при условии, что преобразования выполняются лишь над строками матрицы.
Системой m линейных уравнений с n неизвестными называется система вида
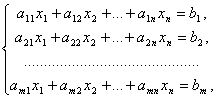
где aij и bi (i=1,…,m; b=1,…,n) – некоторые известные числа, а x1,…,xn – неизвестные. В обозначении коэффициентов aij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.
Коэффициенты при неизвестных будем записывать в виде матрицы 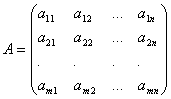 , которую назовём матрицей системы.
, которую назовём матрицей системы.
Числа, стоящие в правых частях уравнений, b1,…,bm называются свободными членами.
Совокупность n чисел c1,…,cn называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел с1,…,cn вместо соответствующих неизвестных x1,…,xn.
Наша задача будет заключаться в нахождении решений системы. При этом могут возникнуть три ситуации:
- Система может иметь единственное решение.
- Система может иметь бесконечное множество решений. Например,
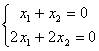 . Решением этой системы является любая пара чисел, отличающихся знаком.
. Решением этой системы является любая пара чисел, отличающихся знаком. - И третий случай, когда система вообще не имеет решения. Например,
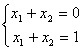 , если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
, если бы решение существовало, то x1 + x2 равнялось бы одновременно нулю и единице.
Система линейных уравнений, имеющая хотя бы одно решение, называется совместной. В противном случае, т.е. если система не имеет решений, то она называется несовместной.
Рассмотрим способы нахождения решений системы.
Правило Крамера
Рассмотрим систему 3-х линейных уравнений с тремя неизвестными:
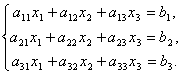
Определитель третьего порядка, соответствующий матрице системы, т.е. составленный из коэффициентов при неизвестных,

называется определителем системы.
Составим ещё три определителя следующим образом: заменим в определителе D последовательно 1, 2 и 3 столбцы столбцом свободных членов
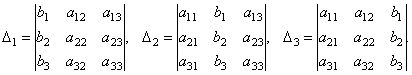
Тогда можно доказать следующий результат.
Теорема (правило Крамера). Если определитель системы Δ ≠ 0, то рассматриваемая система имеет одно и только одно решение, причём
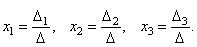
Доказательство. Итак, рассмотрим систему 3-х уравнений с тремя неизвестными. Умножим 1-ое уравнение системы на алгебраическое дополнение A11 элемента a11, 2-ое уравнение – на A21 и 3-е – на A31:
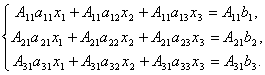
Сложим эти уравнения:
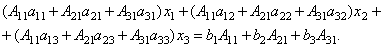
Рассмотрим каждую из скобок и правую часть этого уравнения. По теореме о разложении определителя по элементам 1-го столбца
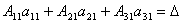 .
.
Далее рассмотрим коэффициенты при x2:
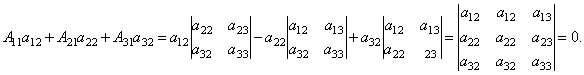
Аналогично можно показать, что и 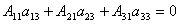 .
.
Наконец несложно заметить, что 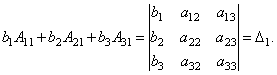
Таким образом, получаем равенство: 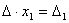 .
.
Следовательно, 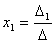 .
.
Аналогично выводятся равенства 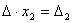 и
и 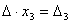 , откуда и следует утверждение теоремы.
, откуда и следует утверждение теоремы.
Таким образом, заметим, что если определитель системы Δ ≠ 0, то система имеет единственное решение и обратно. Если же определитель системы равен нулю, то система либо имеет бесконечное множество решений, либо не имеет решений, т.е. несовместна.
Примеры.Решить систему уравнений
Итак, х=1, у=2, z=3.
- Решите систему уравнений при различных значениях параметра p:
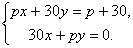
Система имеет единственное решение, если Δ ≠ 0.
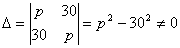 . Поэтому
. Поэтому 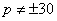 .
.
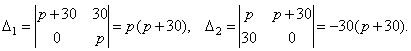
- При
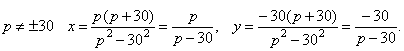
- При p = 30 получаем систему уравнений
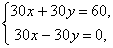 которая не имеет решений.
которая не имеет решений. - При p = –30 система принимает вид
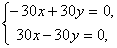 и, следовательно, имеет бесконечное множество решений x=y,yÎR.
и, следовательно, имеет бесконечное множество решений x=y,yÎR.
Метод Гаусса
Ранее рассмотренные методы можно применять при решении только тех систем, в которых число уравнений совпадает с числом неизвестных, причём определитель системы должен быть отличен от нуля. Метод Гаусса является более универсальным и пригоден для систем с любым числом уравнений. Он заключается в последовательном исключении неизвестных из уравнений системы.
Вновь рассмотрим систему из трёх уравнений с тремя неизвестными:
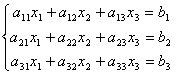 .
.
Первое уравнение оставим без изменения, а из 2-го и 3-го исключим слагаемые, содержащие x1. Для этого второе уравнение разделим на а21 и умножим на –а11, а затем сложим с 1-ым уравнением. Аналогично третье уравнение разделим на а31 и умножим на –а11, а затем сложим с первым. В результате исходная система примет вид:
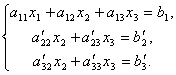
Теперь из последнего уравнения исключим слагаемое, содержащее x2. Для этого третье уравнение разделим на 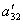 , умножим на
, умножим на 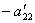 и сложим со вторым. Тогда будем иметь систему уравнений:
и сложим со вторым. Тогда будем иметь систему уравнений:
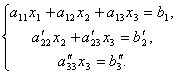
Отсюда из последнего уравнения легко найти x3, затем из 2-го уравнения x2 и, наконец, из 1-го – x1.
При использовании метода Гаусса уравнения при необходимости можно менять местами.
Часто вместо того, чтобы писать новую систему уравнений, ограничиваются тем, что выписывают расширенную матрицу системы:

и затем приводят её к треугольному или диагональному виду с помощью элементарных преобразований.
К элементарным преобразованиям матрицы относятся следующие преобразования:
- перестановка строк или столбцов;
- умножение строки на число, отличное от нуля;
-
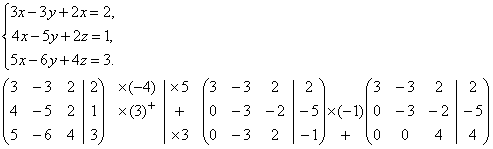 прибавление к одной строке другие строки.
прибавление к одной строке другие строки.
Примеры: Решить системы уравнений методом Гаусса.
Вернувшись к системе уравнений, будем иметь
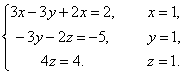
Выпишем расширенную матрицу системы и сведем ее к треугольному виду.

Вернувшись к системе уравнений, несложно заметить, что третье уравнения системы будет ложным, а значит, система решений не имеет.
Разделим вторую строку матрицы на 2 и поменяем местами первый и третий столбики. Тогда первый столбец будет соответствовать коэффициентам при неизвестной z, а третий – при x.
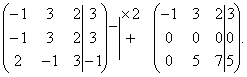
Вернемся к системе уравнений. 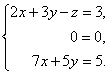
Из третьего уравнения выразим одну неизвестную через другую и подставим в первое.
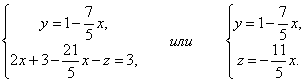
Введение в математический анализ
Понятие функции, свойства функций
Определение:Пусть даны два числовых множества X и Y. Функцией называется правило, по которому каждой переменной 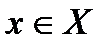 соответствует одно и только одно значение
соответствует одно и только одно значение 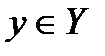 .
.
Функция обозначается 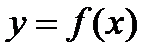 или
или 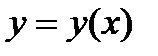 или
или 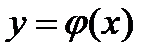 .
.
Переменная x – независимая переменная или аргумент функции; переменная y – зависимая переменная или значение функции.
Определение: Множество всех значений независимой переменной x , при которых функция существует, называется областью определения функции и обозначается D(y).
Определение: Множество всех возможных значений зависимой переменной y называется областью значений функции и обозначается E(y).
Используют следующие способы задания функции:
1.Аналитический способ – задание функций с помощью формул. Например: 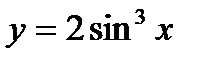 ,
, 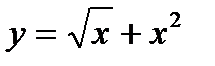 .
.
2.Графический способ – задание функций с помощью графика. Например:
| y x |
| y x |
3.Табличный способ – задание функций с помощью таблиц. Например:
| x | -3 | -2 | -1 | |||
| y |
4. Словесный способ – задание функций с помощью алгоритма вычисления. Например:
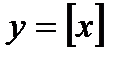 - целая часть числа х.
- целая часть числа х.
Целая часть числа х – это ближайшее целое число, не превосходящее самого числа х.
Свойства функций приведены в таблице:
| Название свойства | Определение | Графическое изображение | |
| Нули функции | Нулём функции называется то значение х, при котором функция обращается в 0, то есть 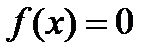 . . |
Нули – это точки пересечения графика функции с осьюОх. | |
| Четность функции | Функция называется чётной, если для любого х из области определения выполняется равенство 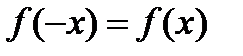 |
Четная функция симметрична относительно оси Оу | |
| Нечет-ность функции | Функция называется нечётной, если для любого х из области определения выполняется равенство  . . |
Нечетная функция симметрична относительно начала координат. | |
| Функция, которая не является ни чётной,ни нечётной, называется функцией общего вида. |
| ||
| Возрас-тание функции | Функция 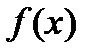 называется возрастающей, если большему значению аргумента соответствует большее значение функции, т.е. называется возрастающей, если большему значению аргумента соответствует большее значение функции, т.е. 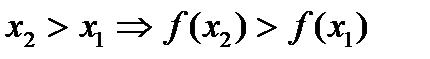 |
| |
| Убывание функции | Функция 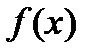 называется убывающей, если большему значению аргумента соответствует меньшее значение функции, т.е. называется убывающей, если большему значению аргумента соответствует меньшее значение функции, т.е. 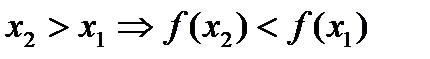 |
| |
| Промежутки, на которых функция либо только убывает, либо только возрастает, называются промежутками монотонности . |
| ||
| Локаль-ный максимум | Точка х0 называется точкой локального максимума, если для любого х из окрестности точки х0 выполняется неравенство: 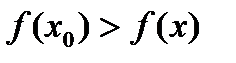 . . |
| |
| Локаль-ный минимум | Точка х0 называется точкой локального минимума, если для любого х из окрестности точки х0 выполняется неравенство: 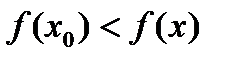 . . |
| |
| Точки локального максимума и точки локального минимума называются точками локального экстремума. |
| ||
| Перио-дичность функции | Функция f(x) называется периодичной, с периодомТ, если для любого х выполняется равенство 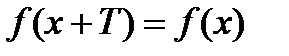 . . |
| |
| Проме-жуткизнакопос-тоянства | Промежутки, на которых функция либо только положительна, либо только отрицательна, называются промежутками знакопостоянства. |
| |
| Непре-рывность функции | Функция 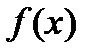 называется непрерывной в точке называется непрерывной в точке 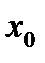 , если предел функции при , если предел функции при |

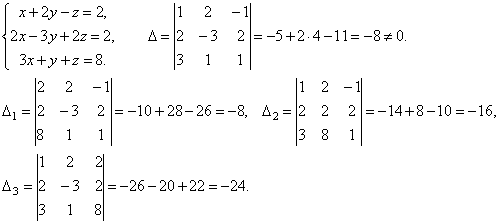
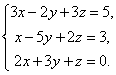
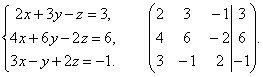
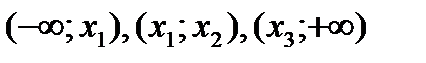
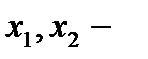 точки локального экстремума.
точки локального экстремума.