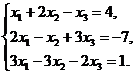Решение системы линейных уравнений методом Гаусса.
При решении системы линейных уравнений часто применяется метод Гаусса. Сущность этого метода поясним на примерах.
- Рассмотрим систему трех линейных уравнений с тремя неизвестными
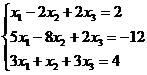
Решение.
Исключим из последних двух уравнений х1. Для этого умножим первое уравнение на -5 и результаты прибавим соответственно ко второму уравнению, затем обе части первого уравнения умножим на -3 и результаты прибавим к третьему уравнению. В результате получим систему, эквивалентную данной:

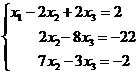 (1)
(1)
Разделив обе части второго уравнения системы (1) на 2, получим систему
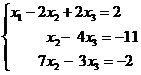 (2)
(2)
Теперь исключим из третьего уравнения системы (2) х2.
Для этого обе части второго уравнения этой системы умножим на — 7 и результаты прибавим к третьему уравнению. В результате получим систему
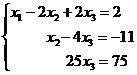 (3)
(3)
Откуда х3 =3, х2=1 и х1=–2. Это решение заданной системы
Приведение данной системы к ступенчатому виду (3) практически более удобно, если использовать преобразования расширенной матрицы данной системы, т. е. матрицы, составленной из коэффициентов при неизвестных и свободных членов. Для удобства столбец свободных членов этой матрицы отделим вертикальной чертой. Расширенная матрица данной системы имеет вид
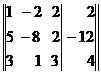 .
.
Умножим элементы первой строки матрицы на — 5 и результаты прибавим к элементам второй строки, затем умножим элементы первой строки на — 3 и результаты прибавим к элементам третьей строки. Получим матрицу
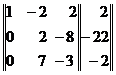 .
.
Разделив элементы второй строки на 2, получим
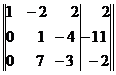 .
.
Элементы второй строки умножим на — 7 и результаты прибавим к элементам третьей строки. Получим матрицу
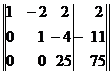 ,
,
которая позволяет данную систему привести к виду (3) и затем решить ее.
- Рассмотрим систему уравнений
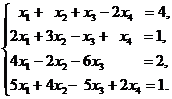
Решение. Составим расширенную матрицу системы:
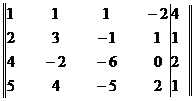
Умножим элементы первой строки последовательно на -2, -4 и -5. Полученные результаты прибавим соответственно к элементам второй, третьей и четвертой строкам. Получим матрицу
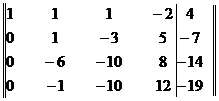
Элементы второй строки умножим на 6 и результаты прибавим к элементам третьей строки, затем элементы второй строки прибавим к элементам четвертой строки. Получим матрицу
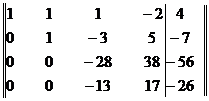
Элементы третьей строки разделим на -2 и затем элементы четвертой строки прибавим к элементам третьей строки. Получим матрицу

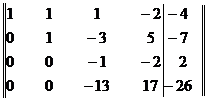
Теперь элементы третьей строки умножим на 13 и результаты прибавим к элементам четвертой строки. Получим матрицу
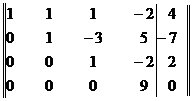
Следовательно, данную систему можно записать так:
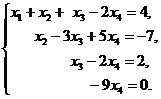
Откуда х4 =0, х3=2, х2=–1 и х1=–3.
Матрицы, получаемые после соответствующих преобразований, являются эквивалентами. Их принято соединять знаком ~ .
Задачи для расчетной работы №2
Часть I
В задачах 1-20 решить данную систему уравнений пользуясь формулами Крамера. Сделать проверку полученного решения.
1. 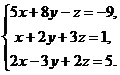 2.
2. 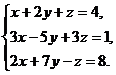
3. 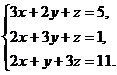 4.
4. 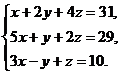
5. 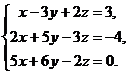 6.
6. 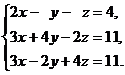
7. 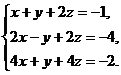 8.
8. 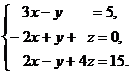
9. 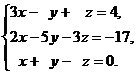 10.
10. 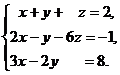
11. 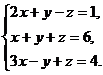 12.
12. 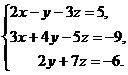
13. 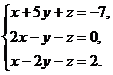 14.
14. 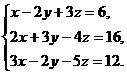
15. 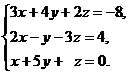 16.
16. 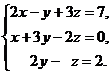
17. 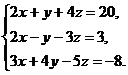 18.
18. 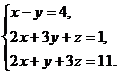
19. 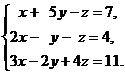 20.
20. 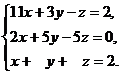
Часть II
В задачах 1-20 систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы. Сделать проверку полученного решения
1. 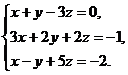 2.
2. 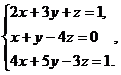
3. 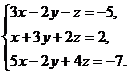 4.
4. 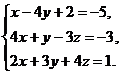
5. 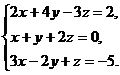 6.
6. 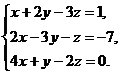
7. 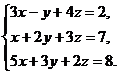 8.
8. 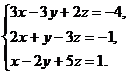
9. 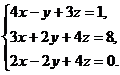 10.
10. 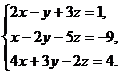
11. 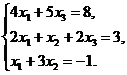 12.
12. 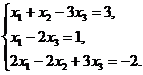
13. 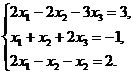 14.
14. 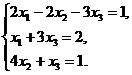
15. 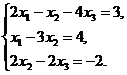 16.
16. 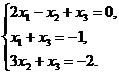
17. 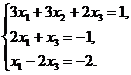 18.
18. 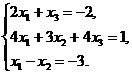
19. 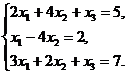 20.
20. 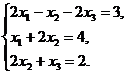
Часть III
В задачах 1-10 решить данную систему уравнений методом Гаусса. Рекомендуется преобразования, связанные с последовательным исключением неизвестных, применять к расширенной матрице данной системы. Сделать проверку полученного решения.
1. 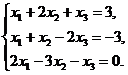 2.
2. 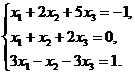
3. 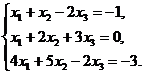 4.
4. 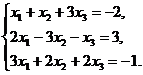
5. 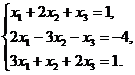 6.
6. 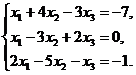
7. 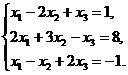 8.
8. 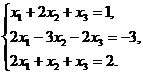
9. 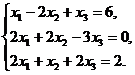 10.
10.