Методы синтеза цифровых СУ ИМ. Метод дискретизации аналоговых регуляторов класса «вход/выход» (метод аналогий). Цифровой ПИД- регулятор.

Методы синтеза цифровых СУ ИМ. Под синтезом СУ ИМ понимают нахождение ее структуры и параметров, обеспечивающих заданное качество управления при известных входных воздействиях.

На практике задачу синтеза начинают с того, что задают структуру и параметры неизменяемой части СУ ЭП. К неизменяемой части СУ ЭП относят ОУ, включающий все тех. средства, преобразующие управляющее воздействие в выходную координату (приводы, передат. механизмы), а также датчики измеряемых координат, устройства преобразования и передачи информации от объекта к устройству управления.

На предварительном этапе синтеза выбирают элементы ОУ из числа типовых изделий, основываясь на основных условиях его функционирования. Далее составляется мат. модель ОУ. После определения неизменяемой части ОУ переходят к синтезу структуры и параметров устройства управления. При этом используют несколько подходов.

Первый подход базируется на задании конкретной структуры устройства управления. Как правило, задаются типовыми регуляторами класса “вход-выход” или простейшими корректирующими звеньями. Корректирующие звенья размещают последовательно с ОУ, в ряде случаев хор. эффект дает установка их в канале обратной связи или на входе системы. Далее решается задача параметрического синтеза, удовлетворяющего требованиям к статике и динамике замкнутой СУ ЭП.

Второй подход основывается на составлении структурной схемы системы управления без задания собственно структуры регуляторов: выбирается число контуров регулирования, их соподчиненность, расположение регуляторов в структуре устройства управления и др. В основе подхода - избранные принципы управления и требования к статическим и динамическим показателям системы. Т.о, при таком подходе посл-но решаются задачи структурного и параметрического синтеза регуляторов.

Третий подход основан на синтезе оптимальных СУ ЭП в смысле заданного критерия качества управления при заданных ограничениях на ресурсы управления. При таком подходе задается формальный критерий качества. Результат синтеза – структура и параметры устройства управления, удовлетворяющих требуемому качеству управления. Системы управления, синтезированные на основе двух первых подходов, часто называют системами со стабилизируемыми показателями качества управления. Системы управления, синтезированные на основе третьего подхода, называют системами с оптимизируемым показателем качества управления.

Метод дискретизации аналоговых регуляторов класса “вход - выход”.Данный метод основан на применении процедур синтеза линейных аналоговых САУ. В качестве критериев оптимальности принимают общепринятые при синтезе таких систем интегральные квадратичные функционалы, а, след-но, динамические процессы в оптимизированных контурах регулирования соот-ют реакциям оптимальных фильтров, напр. фильтров Баттерворта n-го порядка. Синтезированное аналоговое устройство управления содержит один или несколько последовательно включенных регуляторов (корректирующих устройств) класса “вход/выход”.

Суть метода заключается в замене передаточных функций синтезированных непрерывных регуляторов их дискретными аналогами. Отсюда и второе название данного метода синтеза – метод аналогий. Для преобразования аналоговых передаточных функций регуляторов в дискретные применяют замену непрерывных операторов p Лапласа их дискретным аналогом z = f(p). В качестве примера рассмотрим дискретизацию непрерывного ПИД-закона регулирования. Процедура преобразования иллюстрируется рис.1. Входным воздействием регулятора является ошибка регулирования (e(t) для непрерывного и e(kT) для дискретного), выходным – сигнал управления (u (t) для непрерывного и u (kT) для дискретного).

Приведенное преобразование основано на замене:

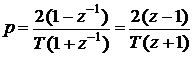- при формировании интегральной составляющей ПИД–закона регулирования;

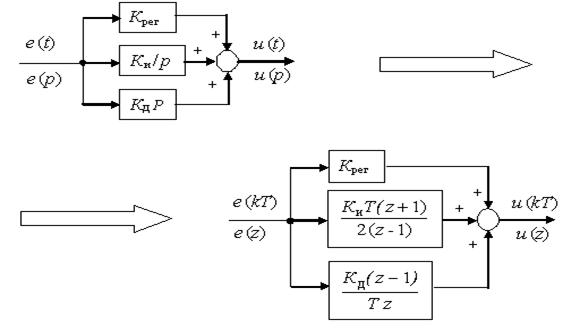
Рис. 1. Преобразование непрерывного ПИД- регулятора в его

дискретный аналог

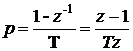- при формировании дифференциальной составляющей ПИД–закона регулирования.

Параметры К_рег , К_и , К_Д получены в результате синтеза аналогового ПИД- регулятора, Т – временной интервал между двумя соседними значениями управляющего воздействия (такт управления).

Применение этого метода синтеза предполагает, что дискретизацией аналоговых сигналов по уровню можно пренебречь, такт управления достаточно мал (как правило, на порядок меньше минимальной постоянной времени объекта управления), а также предполагатся что периоды прерывания Т импульсного элемента датчиков обратной связи и регуляторов одинаковы и неизменны, причем синхронизированы во времени.

Применительно к цифровым электромеханическим САУ такт прерывания не должен превышать 0,005 с. Обеспечение этих условий позволяет получить динамические характеристики цифровой САУ практически такие же, что и в непрерывной системе.

39. Типовая методика структурно-параметрического синтеза контуров регулирования СУ ИМ по желаемой передаточной функции. Привести пример.

Рассматриваемая методика широко применяется при синтезе систем подчиненного регулирования координат электроприводов и базируется на компенсации больших постоянных времени (БПВ) объекта упр-я устр-ом упр-я. Послед-ть этапов синтеза:

1. Структурно-параметрическая декомпозиция объекта управления.

Линейный объект управления разбивают на n последовательно соединенных динамических звеньев с одним или двумя доминирующими полюсами (апериодические первого-второго порядка и интегрирующие); в объект регулирования каждого контура последовательно включают фильтр (апериодическое звено первого порядка) с эквивалентной малой постоянной времени (ЭМПВ) T_m,i, i = 1,…, n; величину эквивалентной малой постоянной времени T_m,i каждого контура регулирования выбирают как минимум в 2 раза больше эквивалентной малой постоянной времени предыдущего контура регулирования, т. е. T_{m , i} ³2T_{m , i-1}, i = 2,…, n .

В результате структурно-параметрической декомпозиции в объекте каждого контура регулирования должны быть выделены 1-2 БПВ и одна ЭМПВ T_{m , i} .

2. Выбор критерия качества регулирования контура.

За критерий качества регулирования каждого контура принимаем желаемую передаточную функцию разомкнутого контура. Для электромеханических СУ ЭП целесообразно применять настройки контуров регулирования на ТО или СО. Желаемую передаточную функцию разомкнутого контура в этом случае записывают в виде:

а) при настройке на ТО:

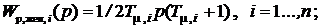, (1)

б) при настройке на СО:

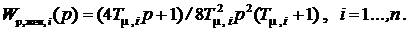
3. Определение структуры и параметров регулятора каждого контура регулирования (структурно-параметрический синтез регуляторов).

Передаточная функция оптимального регулятора i–го контура определяется в виде:

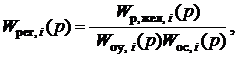(2) где W_{оу, i} (p) – передаточная функция объекта регулирования, входящая в i – й контур регулирования;

W_{ос, i} (p) – передаточная функция звена отрицательной обратной связи i-го контура регулирования.

Далее производится расчет численных значений параметров синтезированных регуляторов (коэффициентов передач, постоянных времени интегрирования, дифференцирования).

4. Выбор элементной базы и расчет параметров принципиальной схемы регулятора каждого контура.

Современные электронные устройства управления непрерывных систем управления реализуют, на основе операционных усилителей в интегральном исполнении. Расчет параметров принципиальной схемы регулятора сводится к расчету численных значений резисторов и конденсаторов во входной цепи и цепи обратной связи операционного усилителя.

Рассмотрим применение рассмотренной методики для синтеза контура регулирования тока якоря электродвигателя постоянного тока. Структурная схема системы регулирования приведена на рис1.

1. ОУ представляет собой 2 аперио-х звена первого порядка, описывающих тиристорный преобразователь (K_тп и T_тп – его параметры) и якорную цепь двигателя. При синтезе контура рег-я тока якоря обр-ой связью по э.д.с. двигателяE_дможно, пренебречь, поскольку скорость ее изменения значительно ниже скорости изменения тока якоря.

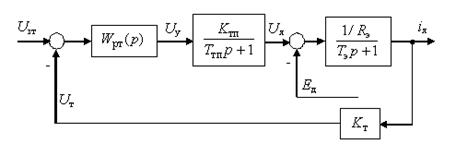
Рис1. Структурная схема контура регулирования тока якоря электродвигателя

К большим постоянным времени объекта управления относится постоянная времени T_э электромагнитной цепи, к малым – постоянная времени T_тп тиристорного преобразователя. Тогда эквивалентная малая постоянная времени контура регулирования тока T_mт = T_тп.

2. Зададимся настройкой контура регулирования тока на ТО, т. е. критерием качества в виде (1).

3. Тогда структура регулятора тока якоря в соответствие с (2) после элементарных преобразований будет иметь вид

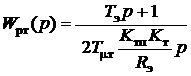, т. е. является пропорционально-интегральной (ПИ).

Параметры этого регулятора:

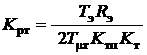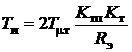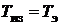, , , причем только 2 из них являются независимыми, поскольку .

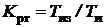4. Для расчета параметров регулятора рассмотрим его принципиальную схему на основе операционного усилителя (рис2.).

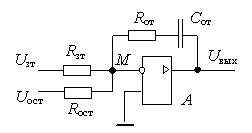
Рис2. Принципиальная схема ПИ-регулятора тока якоря

Заметим, что принципиальная схема регулятора содержит 4 элемента R_зт , R_от , R_ост и С_от, значения которых неизвестны, однако в распоряжении проектировщика имеется лишь 2 параметра регулятора (см. п. 3). Зададимся значением емкости С_от, например С_от = 1 мкф. Тогда R_ост = T_э / С_от , R_зт = R_ост / K_рт .

Поскольку сумма входных токов операционного усилителя в потенциально нулевой точке M (см. рис.2) равна нулю, то 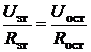. Отсюда 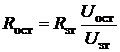, где U_зт , U_ост – напряжения задания и обратной связи по току, соответствующие максимально допустимому току якоря.

39. Типовая методика структурно-параметрического синтеза контуров регулирования систем управления по желаемой передаточной функции. Привести пример синтеза.

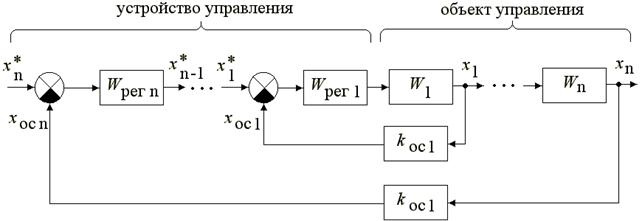
Методика использует принцип подчинённого регулирования координат с вложенными друг в друга контурами регулирования и состоит из 4-х этапов: