Ф-ция распределения вероятностей

Функцией распределения случайной величины Х называется функция F(x), выражающая для каждого х вероятность того, что CB Х примет знач-е < х:

F(x)=P(X<x).

Cв-ва:1)0≤F(x)≤1.

2)F(x2)≥F(x1).

3)F(x)в точке x₀ непрерывна слева 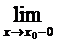=F(x₀).

4)limF(x)(x→-∞)=0 и limF(x)(x→+∞)=1.

5)P(X=x₀)=F(x₀+0)-F(x₀-0)=F(x₀+0)-F(x₀).

6)P(a≤X<b)=F(b)-F(a).

14.Плотность распределения вероятностей:

р(х)=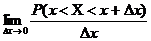

Функция р(х) называется плотностью распределения вероятностей. График функции р(х) называется кривой распределения.

Свойства ПРВ:

1) F(x)=P(X<x)= 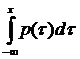,т.е сущ-ет так называемая интегральная связь между функциями р(х) и F(х). Функцию F(х) иногда называют интегральной

функцией распределения или интегральным законом распределения.

2. Следовательно, если функция р(х) непрерывна в точке x , то функция

распределения F(х) дифференцируема в этой точке, причем

р(х)=F’(х), т.е. сущ-ет так называемая дифференциальная связь

между функциями р(х) и F(х) . Следует отметить, что плотность распределения

р(х) называют также дифференциальной функцией распределения.

3. т.к. F(x)-неубыв ф-ция, р(х)>или= при всех х.

4.

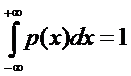
МО СВ

Мат.ожиданием ДСВ называется сумма произведений ее возможных значений на соответствующие им вероятности:

М(Х)=х1р1+х2р2+…хnрn= .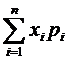

Св-ва: 1)а≤М(Х)≤b.

2)M(C)=C.

3)M(CX)=CM(X).

4)M(XY)=M(X)*M(Y).

5)M(X+Y)=M(X)+M(Y)

Мат.ожиданиемHСВ:

M(X)=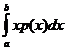

Если значения НСВ Х принадлежат бесконечному интервалу (- 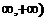, то ее

математическое ожидание определяется формулой

М(Х)= .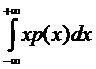

Свойства те же, что и для ДСВ.

Разность Х-М(Х) наз-ся отклонением СВ Х от её М(Х). Отклонение является случайной

величиной. Покажем, что математическое ожидание отклонения равно нулю.

Действительно, М(Х-М(Х))=М(Х)-М(М(Х))=М(Х)-М(Х)=0

Это равенство объясняется тем, что отклонения могут быть как положительными, так и отрицательными; в результате их взаимного погашения среднее значение отклонения равно нулю.

16.Дисперсия СВ– мат. ожидание квадрата ее отклонения от мат. ожидания:

D(X)=M(X-M(X))²=M(X²)-M²(X).

Св-ва:1) дисперсия постоянной величины С равна нулю:

D(C)=0;

2) Постоянный множи

3)

4) тель можно выносить за знак дисперсии, возведя его в квадрат:

D(CX)=C²D(X);

3) Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:

D(X+Y)=D(X)+D(Y)

4) Дисперсия разности двух независимых случайных величин равна сумме

их дисперсий:

D(X – Y) = D(X) + D(Y).
Ср.квадратич.отклон-ем σ СВ Х наз-ся квадратный корень из дисперсии:σ=кореньD(X)

18.БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ И ЕГО ХАР-КИ!!

Ряд распределения бином з-на имеет вид:

xi				…	m	…	n
pi	q	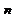C	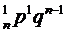C	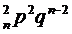…	C	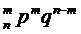…	p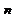

Т-ма: Мат. ожидание и дисперсия СВХ,распределенной по биномиальному закону, вычисляются соответственно по ф-лам:

M(X)=np; D(X)=npq;

Док-во:

Доказательство. СВ Х–число наступлений события А в n независимых испытаниях–можно представить в виде суммы n независимых величин Х=Х1+Х2+…+Хn= 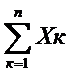, каждая из которых имеет один и тот же з-н распределения:

xi
pi	q	p

СВ Хк, которую называют индикатором события А, выражает число наступлений события A в k-м испытании k=1,2,…,n , т.е. при наступлении события A Xk=1 с вероятностью p, при ненаступлении A Xk=0 c вер-стью q.

Найдем числовые характеристики индикатора события A:

M(X)=x1p1+x2p2=1*p+0*q=p

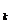D(X )=x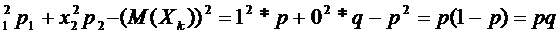

Таким образом, математическое ожидание и дисперсия рассматриваемой СВ X:

М(Х)=М(Х1+Х2+…+Хn)=р+р+…+р=np

D(X)=D(X1+X2+…+Xn)=pq+pq+…+pq=npq.

Распределение Пуассона

Рассмотрим дискретную случайную величину Х, принимающую только целые неотрицательные значения (0, 1, 2,…, m,…), последовательность которых бесконечна, но счетна. Такая случайная величина называется распределенной по закону Пуассона, если вероятность того, что она примет значение m,выражается формулой Пуассона:
P(X=m)=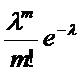

Где λ-параметр закона Пуассона(положит величина) .

xi				…	m	…
pi	e			…		…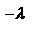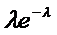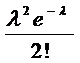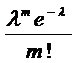

Очевидно, что определение закона Пуассона корректно, так как основное

свойство ряда распределения выполнено, ибо сумма всех вероятностей

равна 1:

+ + + +…=

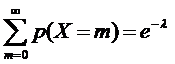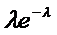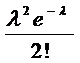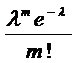=e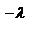

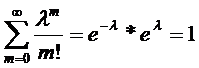
Мат.ожидание и дисперсия СВ Х,распределенной по закону Пуассона, вычисляются соответственно по формулам:

M(X)= λ;D(X)=λ;

Т-ма: Сумма двух независимых СВ, подчиняющихся распр-ю Пуассона с параметрами λ1 и λ2, также имеет распределение Пуассона с параметром λ1+λ2.