Численные методы решения систем линейных уравнений (СЛАУ): метод простых итераций.

Способ итераций дает возможность получить последовательность приближенных значений, сходящихся к точному решению системы.

Рассмотрим систему из n линейных уравнений с n неизвестными:

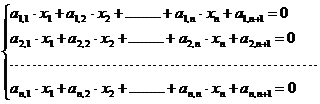(3.8)

Разрешим первое уравнение относительно x₁, второе относительно x₂ и т.д. Тогда систему (3.8) можно переписать в виде:

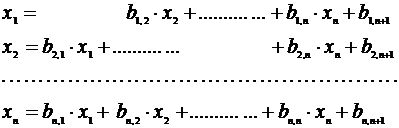(3.9)

где 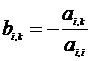(i=1,...,n, k=1,..., n+1)

Правые части системы (3.9) являются функциями переменных x₁, x₂,..., x_n. Обозначив правы части уравнений через L_i(x₁, x₂, ...., x_n) , систему (3.9) можно представить в виде:

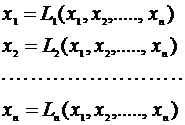(3.10)

Итерации начинаются с задания начального приближенного решения x⁰₁, x⁰₂, ... , x⁰_n , которое может быть получено из физических или других разумных соображений. Чем ближе исходное приближение к решению, тем меньше итераций необходимо для его получения.

Для заданных начальных приближений x⁰₁, x⁰₂, ... , x⁰_n после подстановки этих значений в правые части системы (3.10) получим первые приближения

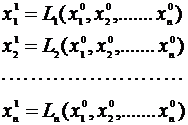(3.11)

Полученные первые приближения могут быть таким же образом использованы для получения 2-х, 3-их и т.д., так что для любого m можно получить m-ое приближение x^m₁, x^m₂, ... , x^m_n.

Итерации проводятся до получения решения с требуемой точностью, которая не должна превышать заданной погрешности вычислений, т.е. окончание итерационного процесса происходит при выполнении следующего неравенства:

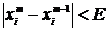,при i=1,2,…n,

где Е – заданная точность решения.

Естественно возникает вопрос об условиях, выполнение которых обеспечивает сходимость полученных приближений к истинному решению системы. Достаточное условие сходимости, т.е. возможности решения СЛАУ методом итераций,формулируется следующим образом.

Для того чтобы итерационный процесс сходился, достаточно, чтобы в любой строке сумма отношений коэффициентов системы к диагональным коэффициентам, взятым из той же строки была строго меньше единицы.

Математически это определение может быть выражено следующим образом:

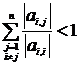
Или, что то же самое,

,

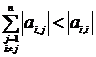т.е. можно сказать, что в любой строке исходной матрицы на главной диагонали должен находиться коэффициент, по абсолютному значению превосходящий сумму модулей остальных коэффициентов.

На первом этапе решения СЛАУ система приводится к виду (3.10) , после чего происходит проверка условия сходимости итерационного процесса к решению системы. Для этого необходимо выбрать максимальные значения коэффициентов a_i,i и провести проверку условия на сходимость итерационного процесса. После этого задаются начальные приближения, обычно для этого используется столбец свободных членов, и проводится расчет по формуле (3.11), которую можно представить в виде

,

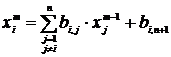до достижения окончательного решения. Здесь используется два вектора переменных: с предыдущими значениями X0 и с последующими значениями X1. В конце каждой итерации производится переприсваивание значений из последующих в предыдущие.