И числовые характеристики случайных величин

Смоленск 2009

Случайной величиной называется величина, которая в результате опыта может принять любые заранее неизвестные значения. Различают дискретные и непрерывные случайные величины.

Дискретной случайной величиной называется такая, значения которой есть конечное или счётное множество фиксированных величин.

Законом распределения вероятностей (рядом распределения) дискретной случайной величины называется последовательность возможных значений случайной величины и соответствующих им вероятностей, причём

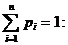
X	x1	x2	…	xn
P	p1	p2	…	pn

Ряд распределения можно задать графически, откладывая на горизонтальной оси значения Х, а на вертикальной - соответствующие им значения вероятностей. Графическое представление ряда распределения называется многоугольником распределения.

Для дискретной случайной величины можно ввести понятие функции распределения F(x), которая равна вероятности случайного события, состоящего в том, что дискретная случайная величина Х примет одно из возможных значений, меньших некоторого значения х, т.е.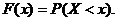

Непрерывные случайные величины характеризуются тем, что их значения могут сколь угодно мало отличаться друг от друга.

Вероятность события X < x (где Х – значение непрерывной случайной величины, а х – произвольно задаваемое значение), рассматриваемая как функция от х, называется функцией распределения вероятностей:

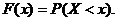
Производная от функции распределения вероятностей называется функцией плотности распределения вероятностей или плотностью вероятности:

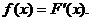
Функция распределения вероятности выражается через плотность вероятности в виде интеграла:

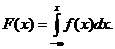
Вероятность попадания случайной величины в интервал (х₁, х₂) равна приращению функции распределения вероятностей на этом интервале:

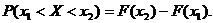
Математическим ожиданием дискретной случайной величины называется сумма вида

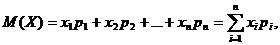
Средним значением или математическим ожиданием непрерывной случайной величины Х называется значение интеграла

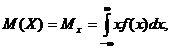
Свойства математического ожидания:

1. M(X)=CM(X); M(C)=C,

где С – произвольная постоянная величина.

2.

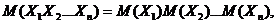
если 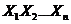– взаимно независимые случайные величины.

3.

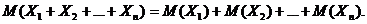
Дисперсией случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

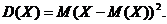
Дисперсию целесообразно вычислять по формуле

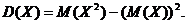
Дисперсией непрерывной случайной величины Х называется значение интеграла

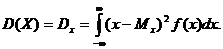
Для определения дисперсии может быть также использована формула

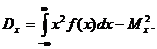
Свойства дисперсии:

1.

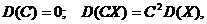
где С – произвольная постоянная.

2.

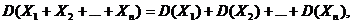
где 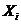– независимые случайные величины.

3.

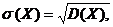
где 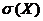- среднее квадратичное отклонение.

Модой Мо(Х) непрерывной случайной величины Х называется такое значение этой величины, плотность вероятности которой максимальна.

Медианой Ме(Х) непрерывной случайной величины Х называется такое ее значение, при котором выполняется равенство