Нормальное распределение и его числовые характеристики.

НСВ (непрерывная случайная величина) называется распределённой по нормальному закону, если её плотность распределения имеет вид:

f(x)= *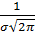

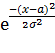
Нормальное распределение определяется двумя параметрами: а – математическое ожидание;

s – среднее квадратическое отклонение.

Функция распределения НСВ имеет следующий вид:

F(х)= *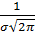

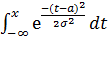
Данный интеграл называется неберущимся,т.е. его нельзя выразить через элементарные функции. Поэтому значение F(x) находятся по таблицам, которые составляются для случая: а=0, =1

Распределение с такими параметрами будет называться нормальным распределением,аего функция распределения будет иметь вид:

Ф(Х)= 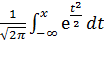– функция Лапласа.

Числовые характеристикинормального распределения:

1.M(x)=a

2.D(x)=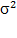

3.s(x)= s

25. Распределениеc².

Пусть имеется несколько нормированных нормально распределённых величин: Х_1, Х_2,….Х_n.

Тогда сумма их квадратов: 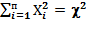^_ является случайной величиной, распределённой по закону « c²»,сk=n степенями свободы.

Плотность такого распределения:

f(x)=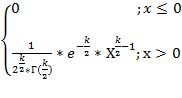

гдеГ(x) – гамма функция

Распределение c² определяется одним параметром К(число данных).

Замечание. С увеличением числа степеней свободы распределение c² приближается к нормальному.

Распределение Стьюдента.

Рассмотрим 2 случайные величины:

Z – нормально распределенная величина;

U – распределенная по закону c² .

Тогда величина T= 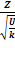имеет распределение, называемое t-распределениеили распределение Стьюдента с К-степенями свободы.

Замечание:с возрастанием числа степеней свободы распределение Стьюдента приближается к нормальному.

Распределение Фишера-Снедекора.

Рассмотрим две случайные величины U и V, распределённые по закону c², со степенями свободы: k₁ и k₂.

Тогда величинаF= 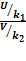будет распределена по закону Фишера-Снедекора.

Замечание. Это распределение определяется 2-мя параметрами: k₁и k₂.

Нормальная кривая и влияние параметров нормального распределения на форму нормальной кривой.

График нормального распределения представляет собой кривую, которая называется нормальной кривой Гаусса.

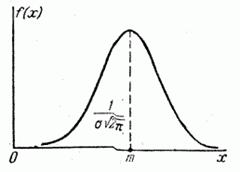
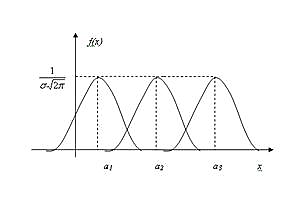
Изменение величины параметра а(математического ожидания) не изменяет формы нормальной кривой, а приводит лишь к ее сдвигу вдоль оси Ox: вправо, если авозрастает, и влево, если аубывает;

Максимум функции плотности вероятностей нормального распределения равен: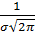

Отсюда следует, что с возрастанием максимальная ордината нормальной кривой убывает, а сама кривая становится более пологой, то есть сжимается к оси Ox; при убывании нормальная кривая становится более “островершинной” и растягивается в положительном направлении оси Oy:

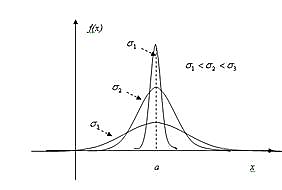
Замечание: при любых значениях параметров а и площадь, ограниченная нормальной кривой и осью Ox, остается равной единице.