Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях.

Будем считать, что производится «n» независимых испытаний, в которых событие А появляется с вероятностью «p».

Найдём вероятность того, что отклонение относительной частоты « » от постоянной вероятности «p» по абсолютной величине не превышает заданного числа : (*)

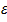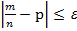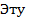вероятность обозначим так:

P ( £ ) (**)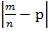

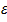Запишем неравенство (*) в виде двойного неравенства:

£

£

£

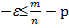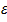
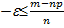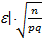
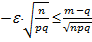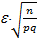
Воспользуемся интегральной теоремой Лапласа:

Х¢=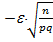

Х²=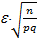

Получим:

P 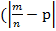£ 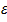) 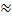2Ф ( )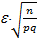

Т. е. вероятность отклонения 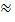удвоенной функции Лапласа.

Наивероятнейшее число наступлений события в независимых испытаниях.

Число « 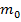» наступления события А в «n» независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события по крайней мере не меньше вероятности других событий. Рассмотрим 2 случая:

1. 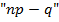– дробное, то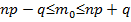

2. 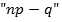– целое, то 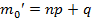и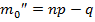

Случаные величины (СВ). Дискретные и непрерывные случайные величины. Ряд распределения дискретных случайных величин.

Случайной величиной называется величина, принимающая в результате опыта одно из своих возможных значений, причём заранее неизвестно, какое именно.

Будем обозначать случайные величины заглавными буквами латинского алфавита: X, Y, Z, …, а их возможные значения соответственно: , , …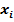

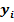Случайные величины подразделяют на 2 группы: дискретные и непрерывные.

Дискретная СВ — если она принимает отдельные изолированные возможные значения с определёнными вероятностями, т.е. эта величина, множество значений которой конечно(счётно).

Непрерывная СВ — если множество её значений целиком заполняет некоторый конечный или бесконечный промежуток.

Для задания ДСВ нужно знать её возможные значения и вероятности, с которыми принимаются эти значения.

Законом распределения ДСВ называется соответствие, устанавливающее связь между возможными значениями ДСВ и вероятностями этих значений. Оно может иметь вид таблицы, формулы или графика.

Таблица, в которой перечислены возможные значения ДСВ и соответствующие им вероятности, называется рядом распределения.

			…		…
			…		…

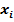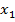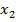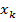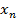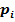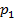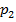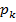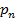Заметим, что событие, заключающееся в том, что СВ примет одно из своих возможных значений, является достоверным. Поэтому: 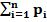=1
Графически закон распределения ДСВ можно представить в виде многоугольника распределения – ломаной, соединяющей точки плоскости с координатами ( , ).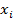

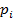р_i

P DVWfu5O38PK+6d+qcntwH9NmNAesjiNHa6+vpscVqERT+gvDD76gQyFMZTixi6oTbcydRC0sZJL4 88WDHOWv1kWu//MX3wAAAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADhAQAAEwAAAAAAAAAA AAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4/SH/1gAAAJQBAAAL AAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQDaY6tfCgIAADsEAAAO AAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAAIQA7fh8R2wAAAAcB AAAPAAAAAAAAAAAAAAAAAGQEAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQABADzAAAAbAUAAAAA " strokecolor="black [3213]">

xi