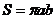Тема 8. Эллипс и окружность. Фокусы, большие и малые оси

1. Эллипс. Геометрическое и аналитическое определение. Их эквивалентность

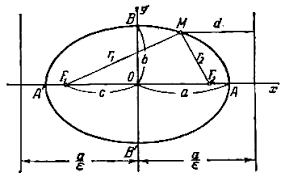
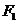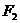Определение (геометрическое).Эллипс – геометрическое место точек на плоскости, сумма расстояний которых до двух данных точек и , называемых фокусами, равна заданному числу 2а.

• Расстояния от Х до F₁ (назовем его r₁) и от Х до F₂ (назовем его r₂) называются фокальными радиусами. .
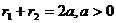• Расстояниемежду фокусами эллипса называется фокусным расстоянием. Эту величину принято обозначать 2с. .

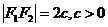При этом из треугольника F₁ХF₂ можно увидеть, что .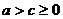

В случае 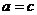получаем отрезок, а в случае 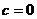- окружность

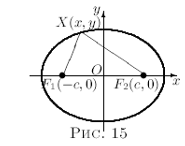
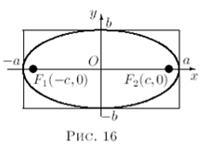
• Введем на данной плоскостисистему координат, которая будет называться канонической для эллипса.
• Каноническое уравнение эллипса: 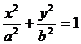, где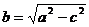

Определение (аналитическое). Эллипс – кривая второго порядка, задаваемая в некоторой прямоугольной системе координат уравнением 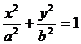, где .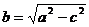

• Наибольшее из чисел а и b называют большой полуосью эллипса,меньшее- малой полуосью эллипса.
• Эллипс проходит через точки 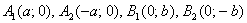, которые называются вершинами эллипса.
• Эллипс заключен в прямоугольник 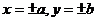, который называется основным прямоугольником эллипса.

При построении эллипса строим основной прямоугольник эллипса и вписываем эллипс в него.

• Отношение 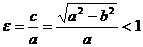называется эксцентриситетом эллипса.
• Директрисами эллипса называются две прямые, уравнения которых в канонической для эллипса системе координат имеют вид 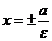. Так как .
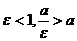• Расстояниемежду директрисами равно .

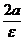Отсюда следует еще одно определение эллипса:

Определение (через директрису).Эллипсом называется геометрическое место точек плоскости, для которых отношениерасстояния до фиксированной точки плоскости, называемой фокусом, к расстоянию до фиксированной прямой, называемой директрисой, есть величина постоянная, меньшая единицы, и называемая его эксцентриситетом: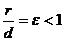

!Параллельный перенос эллипса:

Уравнение 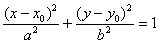задаёт эллипс с большой полуосью «а», малой полуосью «бэ» и центром симметрии в точке .

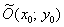Пример.

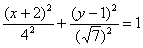
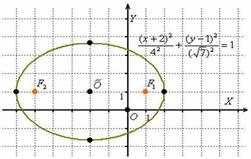
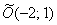
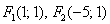
1. Окружность как частный случай эллипса. Полуокружность

+полуэллипс. Пересечение окружностей

Эллипс при a=b превращается в окружность, оба фокуса срастаются с центром, эксцентриситет обнуляется, а директрисы вырождаются.

Если из уравнения окружности (эллипса) выразить одну из переменных, получится два корня, каждый из которых задает верхнюю/нижнюю/правую/левую полуокружность (полуэллипс).

Из планиметрии: при касании двух окружностей (внешним или внутренним образом) точка касания лежит на прямой, соединяющей центры этих окружностей. При этом расстояние между центрами равно сумме радиусов окружностей в ситуации внешнего касания и разности радиусов в ситуации внутреннего касания.

1. Обобщение по кривым второго порядка

Фигура	Уравнение	с	Фокусы	Эксцентриситет	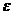Директрисы
Парабола		-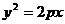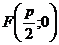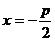
Гипербола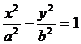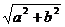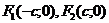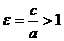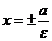
Эллипс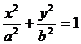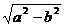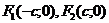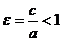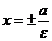
Окружность					-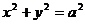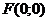

Общее свойство для кривых второго порядка:

Отношениерасстоянияот точки кривой второго порядка (отличной от окружности) до фиксированной точки плоскости, называемой фокусом, к расстоянию до фиксированной прямой, называемой директрисой (ближайшей, если их две), есть величина постоянная и равнаяэксцентриситету.

1. Длина окружности, площадь круга и эллипса

• Длина дуги равна произведению радиуса окружности на радианную меру дуги:
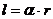
• Длина окружности равна произведению радиуса окружности на :
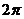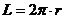
• Площадь круга равна произведению квадрата радиуса окружности на число : .
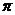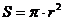• Площадь сектора равна половине произведения квадрата радиуса окружности на радианную меру дуги: .
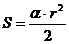• Площадь сегмента равна половине произведения квадрата радиуса окружности на разность радианной меры дуги с её синусом: .
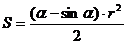• Площадь эллипса с большой полуосьюа и малой полуосью b равна: