Уравнение Лапласа (эллиптическое уравнение)

Это уравнение описывает некоторое установившееся стационарное состояние в пространстве (x,y) в некоторой области G (16.1):

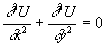(x,y)Î G. (16.1)

Если область G является замкнутой и на границе этой области G задается значение искомой функции:

U(x,y)=j (x,y), (x,y) Î G

то такая задача называется задачей Дирихле.

Для замены этой задачи разностной задачей наложим на область G сетку из прямых, параллельных осям координат с шагом h>0. Точки пересечения этих прямых будут образовывать узлы . Узлы, которые вместе со своими четырьмя ближайшими соседями будут принадлежать области G, называются внутренними узлами. Граничные узлы – это совокупность точек, у которых хотя бы одна из ближайших точек лежит вне области G.

Внутренние узлы будут образовывать некоторую сеточную область G_c , а граничные некоторую сеточную область Г_с.

Для замены дифференциального уравнения заменим производные центральными конечными разностями:

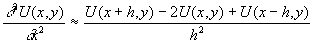
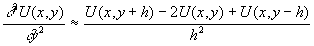
Тогда вместо уравнения (16.1) будем иметь:

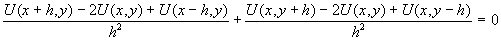
Следовательно, U(x,y) можно выразить в следующем виде:

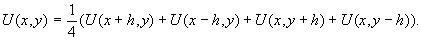
Однако, чтобы иметь возможность оценить точность такой замены, следует идти по несколько иному пути, используя для получения конечно-разностного уравнения формулу Тейлора:

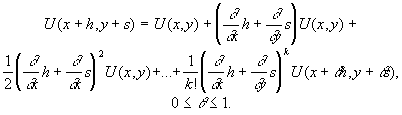
При этом можно воспользоваться разными схемами.

Первая схема. Рассмотрим точку A и ближайшие к ней соседние точки B,C,D,E с координатами A=(x,y), B=(x-h,y), C=(x+h,y), D=(x,y+h), E=(x,y-h). Согласно формуле (4) при k=4, s=h получим:

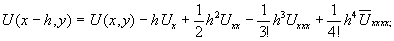
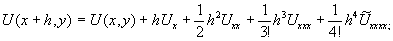
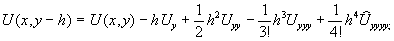
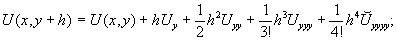
Здесь 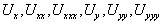-значения производных функции U(x,y) в точке (x,y), а 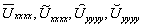- значения производных в некоторых промежуточных точках. Складывая эти значения получаем:

,

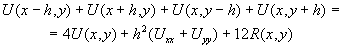где остаточный член R определяется равенством:

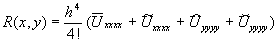
т.е. имеет четвертый порядок малости .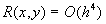

Заметим, что выражение 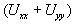является оператором Лапласа:

,

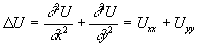поэтому из выражения можно получить выражение:

,

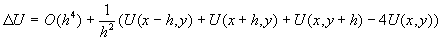которое называется первой основной конечно-разностной формой оператора Лапласа. Путем приравнивания этого выражения нулю и отбрасывания члена O(h⁴) можно получить соотношение.

Вторая схема. Рассмотрим дальние соседние точки около точки:

A=(x,y). Это будут точки B=(x-h,y+h), C=(x+h,y+h),

D=(x+h,y-h), E=(x-h,y-h).

Как и в первой схеме воспользуемся выражением (3) для разложения функции в ряд Тейлора в точках B,C,D,E:

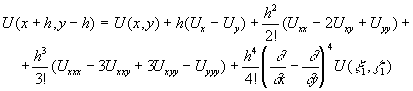
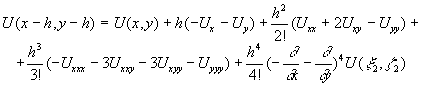
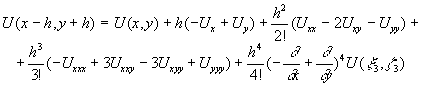
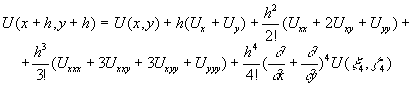
Здесь 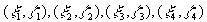некоторые промежуточные точки. Сложив эти выражения будем иметь:

,

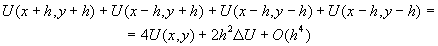откуда можно получить вторую конечно-разностную форму оператора Лапласа:

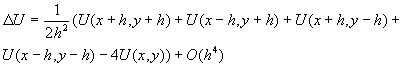
Отбрасывая остаточный член получаем уравнение вида

.

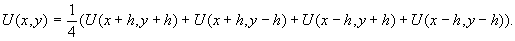Таким образом, в результате применения двух различных схем установлено, что любая внутренняя точка может быть вычислена как среднеарифметическое своих дальних или ближних соседних точек.

Соотношение справедливо для каждой точки области G, поэтому оно будет справедливо для любой внутренней точки (x_i,y_j)Î G_c. Введя обозначение 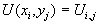и получим систему уравнений:

;

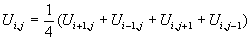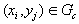
Дополним эту систему уравнениями для граничных точек:

.

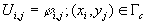Полученная система линейных уравнений, может быть решена любым из методов приведенных в лекции 2, но поскольку эта система имеет достаточно большую размерность (при сетке 105 10 имеем 100 уравнений) и очень разрежена (в каждом из уравнений участвуют не более пяти неизвестных), для решения таких систем рекомендуется использовать итерационные методы, а алгоритм построить так, чтобы не выполнять действий над нулевыми элементами матрицы коэффициентов. Простейшим способом будет задание некоторого начального приближения для внутренних точек 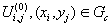и вычисление следующего приближения методом простых итераций:

,

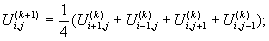При использовании итерационных методов необходимо задавать начальное приближение для значений всех внутренних узлов. От близости этого приближения к истинному решению задачи зависит время расчета. Для уменьшения этого времени используют подход предложенный Либманом и заключающийся в следующем.

Строится сетка с достаточно большим шагом и решается система уравнений небольшой размерности. В результате находится некоторое грубое приближение к решению задачи в узлах сетки. Для получения более точного решения шаг сетки уменьшается вдвое и решается система вчетверо большей размерности. Для сокращения времени расчета в качестве начального приближения для системы с мелкой сеткой используются значения, полученные в результате решения системы с крупной сеткой, а в тех узлах мелкой сетки, которые не совпадают с узлами крупной сетки используется аппроксимация.. Такой процесс деления шага сетки можно выполнить несколько раз, получая все более точное решение поставленной задачи.