Первая производная. Двухточечные методы

Для двухточечных методов при вычислении производных используется значение функции в двух точках. Приращение аргумента задается тремя способами, откладывая Δx = h вправо, влево и в обе стороны от исследуемой точки. Соответственно получается три двухточечных метода численного дифференцирования (табл. 11.1):

Таблица 11.1 Три двухточечных метода численного дифференцирования

метод 1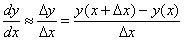
метод 2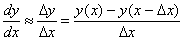
метод 3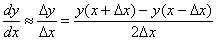

Суть указанных методов проиллюстрирована на рисунке (рис. 11.1). Численное значение тангенса угла α образованного касательной к графику y(x) и осью абсцисс, показывает точное значение производной (геометрический смысл производной). Тангенсы углов α₁, α₂, α₃ соответствуют приближенным значениям производных, определенных методами 1, 2, 3 соответственно (подумайте почему?).

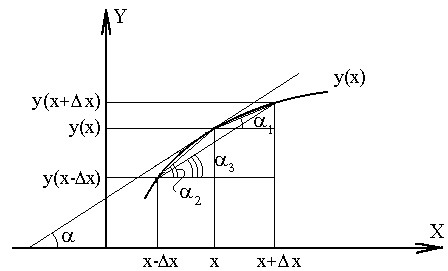
Рис. 11.1 - двухточечные методы численного дифференцирования

ПРИМЕР.

Вычислить точное и приближенное (тремя методами) значения производной функции y=x*x в точке x=1 с шагом h=1 и h=0.001.

Аналитическое решение: y'=2x , y'(1)=2,

Численное решение для шага: h=1

,

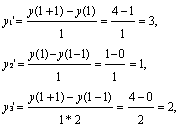для шага h=0.001

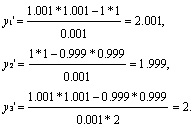
Вычисление первых производных по трёхточечным схемам

Расчетные формулы для указанной трехточечной схемы имеют вид:

Вычисление производных второго порядка

Вторая производная вычисляется как первая производная от первой производной. Для следующей пятиточечной схемы (рис. 11.2):

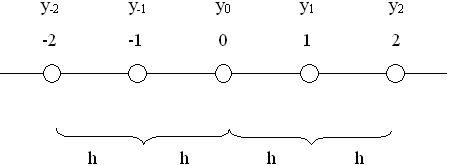
Рис. 11.2 - пятиточечная схема

расчетная формула имеет вид:

ПРИМЕР.

Написать программу для нахождения второй производной функции y = 2 * x⁴

в точке x=1 с шагом h=0.01, сравнить с точным значением.

Аналитическое значение

.

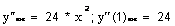Приближенное значение

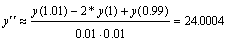
Структура программы (ртабл. 11.2):

Таблица 11.2 - Структура программы

Описание x,y,h

X=1; h=0.01

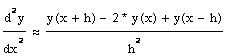Вывод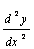

Вычисление производных третьего порядка

Производные третьего порядка вычисляются как первая производная от производной второго порядка. Для рассмотренной пятиточечной схемы расчетная формула имеет вид:

Задание для самостоятельной работы

1. Вычислить значение производной в произвольной точке x=x₀ аналитически и численно тремя методами для пяти значений приращения аргумента Δx=1; 0.2; 0.1; 0.01; 0.001. Результаты расчета вывести на экран и распечатать в виде таблицы

Таблица вывода результатов расчета:

Δx	y(x)	y'(x)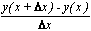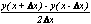
0.2
0.1
0.01
0.001

Варианты функций:

Вар.	Вид функции	Вар.	Вид функции
	x(t)=Ae-at sin(ωt+b)		y=ctgm (ax)
	x(t)=Aeat cos(ωt+b)		y(x)=(eax-e-ax)n
			x(t)=tat
	уυ(t)=cos2(at+b)		y(x)=(ax)sin(bx)
	yυ(t)=sin2(at+b)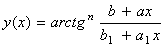
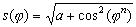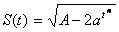	q(t)=(a-btn)n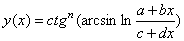
	y(x)=xncos(ax)		R(φ)=arccosm(a+bφn)
			r(φ)=csin(aφ+b)
			y(x)=ln(tgn(ax+b))
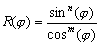			vυ(t)=loga(tn+bm)k
	S(φ)=Вcоsn(aφ+b)		S(φ)=Asinn(aφ+b)
	y=tgax( x/a )		X(t)=lg(atn+b)

Примечание. Значение параметров a, b, c, d, m, n, A, B выбрать самостоятельно.

Численное интегрирование

Определенным интегралом функции f(x), взятом в интервале от a до b, называется предел, к которому стремится интегральная сумма при стремлении всех промежутков ∆x_i к нулю:

.

При приближенном вычислении определенного интеграла шаг интегрирования h=∆x выбирается конечным: , где I_i - элемент интегральной суммы. Заменяя подынтегральную функцию на каждом шаге отрезками линий нулевого, первого и второго порядков, получаем приближенные формулы для вычисления интеграла методами прямоугольников, трапеций и Симпсона соответственно.

1. Приближенные формулы для вычисления интеграла методом прямоугольников (рис 12.1).

Рис. 12.1 - вычисление интеграла методом прямоугольников

Правило прямоугольников (n=0). Заменяем график функции F(x) горизонтальной линией (линий нулевого порядка) и вычисляем значение элемента интегральной суммы как площадь прямоугольника

, где h - шаг интегрирования, у₀ - значение функции в точке х=х₀

у(х₀)=у₀

2. Приближенные формулы для вычисления интеграла методом трапеций (рис. 12.2).

Рис. 12.2. - вычисление интеграла методом трапеций

Правило трапеций (n=1). Заменяем график функции F(x) прямой, проходящей через две точки (х₀,у₀) и (х₀+h,у₁), и вычисляем значение элемента интегральной суммы как площадь трапеции

3. Приближенные формулы для вычисления интеграла методом Симпсона (рис. 12.3).

Рис. 12.3. - вычисление интеграла методом Симпсона

Правило Симпсона (n=2). Заменяем график функции F(x) квадратичной параболой, проходящей через три точки с координатами (х₀,у₀), (х₀+h,у₁), (х₀+2h,у₂). Расчетную формулу для вычисления элемента интегральной суммы получим, используя интерполяционный многочлен Лагранжа, в виде: y(x)=y₀A₀(x)+y₁A₁(x)+y₂A₂(x), где:

При x₀=0; x₁=h; x₂=2h, получим:

При интегрировании на отрезке [a,b] расчетные формулы для методов прямоугольника, трапеций и Симпсона имеют вид:

,

где h - шаг по x, f_a, f_i, f_b - значения функции при x равном a, x_i, b соответственно.

Для метода прямоугольников приведены две расчетные формулы, так как площадь прямоугольника на каждом шаге интегрирования может определяться по левой или правой стороне. Суть метода прямоугольников для отрезка [a, b] проиллюстрирована на рисунке, при этом площадь под кривой f(x) (вспомните геометрический смысл определенного интеграла) заменена суммой площадей заштрихованных прямоугольников (рис. 12.4).

Рис. 12.4 - суть метода прямоугольников для отрезка [a, b]

Задание для самостоятельной работы

1. Вычислить значение определенного интеграла аналитически и численно четырьмя методами для пяти значений N, где N – число разбиений интервала интегрирования N=10; 20; 50; 100; 1000. Результаты расчета вывести на экран и распечатать в виде таблицы. Представление результатов расчета:

N	Аналит. Значение	Метод прямоуг. 1	Метод прямоуг. 2	Метод трапеций	Метод Симпсона

2. Построить графики функций I=F(N).

Варианты интегралов приведены в таблице:

Вар.	Вид интеграла	Вар.	Вид интеграла