Решение систем линейных алгебраических уравнений прямыми методами

ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

Учебное пособие

Работа выполнена на кафедре "Микропроцессорные системы" при реализации приоритетного национального проекта "Образование"

Таганрог 2007

УДК 681.326-3

Синютин С.А. Вычислительная математика (Часть 2). Учебное пособие. – Таганрог: Изд-во ТТИ ЮФУ, 2007. – 71 с.

Работа выполнена в рамках приоритетного национального проекта "Образование" на кафедре "Микропроцессорные системы" ТТИ ЮФУ при реализации образовательного проекта «Разработка образовательных контентов и ресурсов нового поколения для подготовки высококвалифицированных кадров, ориентированных на проектирование интеллектуальных микропроцессорных модулей и построение на их основе высокопроизводительных локальных и распределенных информационных систем мониторинга и диагностики».

В пособии рассматриваются математические методы и алгоритмы, применяющиеся во многих инженерных приложениях. В работе изучаются основные алгоритмы численного интегрирования, дифференцирования, решения обыкновенных и дифференциальных уравнений и систем уравнений.

Работа содержит примеры, иллюстрирующие, как данные концепции используются при инженерном проектировании.

Учебное пособие предназначено для студентов дневной и безотрывной форм обучения специальностей 230201 «Информационные системы и технологии» и 210106 «Промышленная электроника».

Табл. 17 Ил. 28. Библиогр.: 20 назв.

ISBN

Технологический институт Южного

федерального университета, 2007

Синютин С.А., 2007

СОДЕРЖАНИЕ

6 Решение систем линейных алгебраических уравнений прямыми методами. 5

6.1 Метод Гаусса с выбором главного элемента по столбцу. 5

6.2 Метод Холецкого. 7

6.3 Метод прогонки. 8

Задание для самостоятельной работы. 10

Вопросы. 10

7 Решение систем линейных алгебраических уравнений итерационными методами. 11

7.1 Метод Якоби. 11

7.2 Метод Зейделя. 12

7.3 Метод простой итерации. 13

Задание для самостоятельной работы. 14

Вопросы. 14

8 Приближение функций. 15

8.1 Постановка задачи приближения функции по методу наименьших квадратов. 15

8.2 Определение параметров эмпирической зависимости. 17

8.3 Многочлены Бернштейна. 18

Задание для самостоятельной работы. 20

Вопросы. 20

9 Интерполяция функций. 21

9.1 Постановка задачи интерполяции функций. 21

9.2 Оценка погрешности интерполяции. 22

Задание для самостоятельной работы. 24

Вопросы. 24

10 Интерполяция сплайнами. 25

10.1 Глобальная и кусочно-полиномиальная интерполяция. 25

10.2 Интерполяция сплайнами. 28

Задание для самостоятельной работы. 30

Вопросы. 31

11 Численное дифференцирование. 32

11.1 Первая производная. Двухточечные методы. 32

11.2 Вычисление первых производных по трёхточечным схемам. 34

11.3 Вычисление производных второго порядка. 34

11.4 Вычисление производных третьего порядка. 36

Задание для самостоятельной работы. 36

12 Численное интегрирование. 38

Задание для самостоятельной работы. 41

13 Решение задачи Коши одношаговыми методами. 43

13.1 Постановка задачи Коши для дифференциального уравнения первого порядка. 43

13.2 Численное решение задачи Коши методом Эйлера. 43

13.3 Оценка погрешности метода Эйлера. 44

13.4 Модификации метода Эйлера. 46

Решение систем дифференциальных уравнений методом Эйлера. 46

Задание для самостоятельной работы. 47

Вопросы. 47

14 Численное интегрирование систем дифференциальных уравнений. 48

Задание для самостоятельной работы. 51

Варианты заданий. 51

15 Преобразование Фурье. 54

15.1 Аппроксимация функции по Фурье. 54

16 РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ. 59

16.1 Уравнение Лапласа (эллиптическое уравнение) 59

17 РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ (продолжение) 64

17.1 Уравнение теплопроводности (параболическое уравнение) 64

Задание для самостоятельной работы. 67

Метод Холецкого

Если матрица системы является симметричной и положительно определенной, то для решения системы применяют метод Холецкого (метод квадратных корней). В основе метода лежит алгоритм специального LU-разложения матрицы A, в результате чего она приводится к виду A= . Если разложение получено, то, как и в методе LU-разложения, решение системы сводится к последовательному решению двух систем с треугольными матрицами: и . Для нахождения коэффициентов матрицы L неизвестные коэффициенты матрицы приравнивают соответствующим элементам матрицы A. Затем последовательно находят требуемые коэффициенты по формулам:

, i = 2, 3, ..., m,

, i = 3, 4, ..., m,

...............

i = k+1, ... , m.

ПРИМЕР 2. Решение системы методом Холецкого.

Пусть

A= b= .

Находим элементы матрицы L:

Таким образом, разложение матрицы A имеет вид:

Последовательно решаем системы и . Решением 1-ой системы является вектор , а решение 2-ой системы вектор .

Ответ:

% Решить систему Ax=b методом Холецкого

% Введём матрицу

A = [81 -45 45; -45 50 -15; 45 -15 38];

% Введём правую часть

b = [531; -460; 193];

% Найдём разложение Холецкого

R = chol(A);

% R'*R*x = b

% Матрица R легко обратима

y = R' \ b;

x = R \ y;

% Проверим решение

A * x - b

>>

ans =

Метод прогонки

Если матрица системы является разреженной, то есть содержит большое число нулевых элементов, то применяют еще одну модификацию метода Гаусса - метод прогонки. Рассмотрим систему уравнений с трехдиагональной матрицей:

Преобразуем первое уравнение системы к виду , где: , . Подставим полученное выражение во второе уравнение системы и преобразуем его к виду: и т.д.

На i-ом шаге уравнение преобразуется к виду: , где , .

На m-ом шаге подстановка в последнее уравнение выражения

дает возможность определить значение :

.

Значения остальных неизвестных находятся по формулам:

, i = m-1, m-2, ..., 1.

ПРИМЕР 4. Решение системы методом прогонки.

Прямой ход прогонки. Вычислим прогоночные коэффициенты:

, ,

,

, ,

,

Обратный ход прогонки. Находим значения неизвестных:

, , ,

Ответ:

.

Задание для самостоятельной работы

1. Методом Гаусса с выбором главного элемента найти решение системы уравнений:
.

2. Найти разложение матрицы:

.

3. Можно ли применять метод Холецкого к системе уравнений, матрица которой имеет вид:

.

4. Подсчитать количество арифметических действий в методе прогонки.

Вопросы

1. Что такое прямые и итерационные методы.

2. С какой целью применяют модификацию метода Гаусса - схему частичного выбора.

3. Для каких систем уравнений применяют метод Холецкого.

4. Запишите формулы для нахождения решения после приведения системы к виду.

5. Сформулируйте алгоритм метода прогонки.

Метод Якоби

Самый простой способ приведения системы к виду удобному для итерации состоит в следующем: из первого уравнения системы выразим неизвестное x₁, из второго уравнения системы выразим x₂, и т. д. В результате получим систему уравнений с матрицей, в которой на главной диагонали стоят нулевые элементы, а остальные элементы вычисляются по формулам:

, i, j = 1, 2, ... n.

Компоненты вектора d вычисляются по формулам:

, i = 1, 2, ... n.

Расчетная формула метода простой итерации имеет вид:

,

или в покоординатной форме записи выглядит так:

, i = 1, 2, ... m.

Критерий окончания итераций в методе Якоби имеет вид:

, где .

Если , то можно применять более простой критерий: окончания итераций

ПРИМЕР 1. Решение системы линейных уравнений методом Якоби.

Пусть дана система уравнений:

Требуется найти решение системы с точностью

Приведем систему к виду удобному для итерации: .

Выберем начальное приближение, например, - вектор правой части.

Тогда первая итерация получается так:

Аналогично получаются следующие приближения к решению.

, ,

Найдем норму матрицы . Будем использовать норму .

Так как сумма модулей элементов в каждой строке равна 0.2, то = 0.2 < 1/2, поэтому критерий окончания итераций в этой задаче .

Вычислим нормы разностей векторов: , .

Так как , заданная точность достигнута на четвертой итерации.

Ответ: x ₁ = 1.102, x ₂ = 0.991, x ₃ = 1.101

Метод Зейделя

Метод можно рассматривать как модификацию метода Якоби. Основная идея состоит в том, что при вычислении очередного (n+1)-го приближения к неизвестному x_i при i >1 используют уже найденные (n+1)-е приближения к неизвестным x₁, x₂, ..., x_{i - 1}, а не n-ое приближение, как в методе Якоби. Расчетная формула метода в покоординатной форме записи выглядит так:

,

i = 1, 2, ... m.. Условия сходимости и критерий окончания итераций можно взять такими же как в методе Якоби.

ПРИМЕР 2. Решение систем линейных уравнений методом Зейделя.

Рассмотрим параллельно решение 3-х систем уравнений:

, , .

Приведем системы к виду удобному для итераций:

, , .

Заметим, что условие сходимости выполнено только для первой системы. Вычислим 3 первых приближения к решению в каждом случае:

1-ая система. , , ,

Точное решение здесь x ₁ = 1.4, x ₂ = 0.2. Итерационный процесс сходится.

2-ая система. , , , - итерационный процесс разошелся.

Точное решение x ₁ = 1, x ₂ = 0.2.

3-я система. , , , - итерационный процесс зациклился.

Точное решение x ₁ = 1, x ₁ = 2.

Пусть матрица системы уравнений A - симметричная и положительно определенная. Тогда при любом выборе начального приближения метод Зейделя сходится. Дополнительных условий на малость нормы некоторой матрицы здесь не накладывается.

Метод простой итерации.

Если A - симметричная и положительно определенная матрица, то систему уравнений часто приводят к эквивалентному виду: x = x - (Ax - b), - итерационный параметр.

Расчетная формула метода простой итерации в этом случае имеет вид: x ⁽ⁿ⁺¹⁾ = x ⁿ - (Ax ⁿ - b).

Здесь B = E - A и параметр > 0 выбирают так, чтобы по возможности сделать минимальной величину .

Пусть и - минимальное и максимальное собственные значения матрицы A. Оптимальным является выбор параметра . В этом случае принимает минимальное значение равное .

ПРИМЕР 3. Решение систем линейных уравнений методом простой итерации.

% Решить систему Ax=b методом простой итерации.

A = [3 -2 0; -2 3 0; 0 0 3];

b = [-21;24;15];

e = eig(A);

% Вычислим итерационный параметр

tau = 2 / (min(e) + max(e));

r = 1;

% Выполняем метод простой итерации с начальным приближением x0

x0 = [0;0;0];

y = x0;

while r > 100 * eps

x = y - tau * (A * y - b);

r = norm(x-y);

y = x;

end

% Проверим полученное значение

A * x – b

>>

ans =

1.0e-013 *

	-0.2842
0.2487

Задание для самостоятельной работы

1. Убедиться в том, что если A- нижняя треугольная матрица с ненулевыми диагональными элементами, то метод Зейделя сходится за одну итерацию.

2. Пусть A - верхняя треугольная матрица с ненулевыми диагональными элементами. Доказать, что метод Зейделя сходится за конечное число итераций и указать, за какое именно.

3. Вывести оценку числа итераций, требуемых для достижения заданной точности в методе Якоби.

Вопросы

1. Сформулируйте достаточное условие сходимости методов Якоби и метода Зейделя.

2. Сформулируйте критерий окончания итераций в методе Якоби.

3. Сформулируйте условия сходимости метода простой итерации и метода Зейделя для случая симметрических положительно определенных матриц.

4. Из каких условий выбирается итерационный параметр в методе простой итерации.

5. Сформулируйте алгоритм нахождения оптимального итерационного параметра в методе простой итерации.

Приближение функций

На практике часто возникает необходимость найти функциональную зависимость между величинами x и y, которые получены в результате эксперимента. Часто вид эмпирической зависимости известен, но числовые параметры неизвестны.

Ниже рассматривается решение задачи приближения многочленами таблично заданной функции по методу наименьших квадратов и по методу интерполяции.

Многочлены Бернштейна

Предположим, что функция 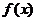задана в отрезке [0,1] в точках , при некотором фиксированном n. В этом случае можно построить многочлен Бернштейна:

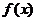Можно доказать, что при многочлены стремятся к функции равномерно по x; кроме того, для любого конкретного целого имеет место предельное соотношение для производных:

Наконец, известно, что если число удовлетворяет неравенству на всем отрезке [0,1], то для любого 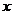из этого отрезка выполняется неравенство: .

Это, конечно, позволяет оценивать ошибку, которая возникает при соответствующей интерполяционной замене.

Сказанное выше для случая функции 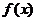одной переменной можно обобщить на случай двух и более переменных. Мы ограничимся обобщением только на случай двух переменных.

Итак, пусть имеется функция на квадрате

,

причем реально она задана в узлах решетки

,

при заранее фиксированных натуральных числах 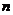и . Построим по этой информации следующий многочлен от двух переменных:

,

где - биномиальные коэффициенты. Это - многочлен Бернштейна для заданной функции на заданной решетке. С его помощью так же можно осуществлять интерполяцию, принимая его значение в той или иной точке квадрата за значение самой функции. Можно доказать, что для любой точки квадрата имеет место неравенство:

,

которое позволяет оценить погрешность интерполяции. (Здесь константы и удовлетворяют в рассматриваемом квадрате неравенствам).

.

Замечание.Случай одной переменной рассматривался выше на отрезке [0, 1], а случай двух переменных - в единичном квадрате. В действительности, рассмотрения возможны на любом отрезке [a,b] и на любом прямоугольнике [a,b;c,d]. Для этого в исходной ситуации (т.е. на произвольном отрезке или на произвольном прямоугольнике нужно сделать линейную замену переменных).

Подробнее: пусть функция 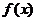задана в точках отрезка , где при некотором фиксированном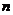

Положим

тогда

если теперь в 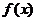положить , то возникнет ситуация функции , заданной уже на отрезке [0, 1]. Аналогично, в случае двух переменных надо сделать замену:

,

после чего возникнет ситуация единичного квадрата.

Задание для самостоятельной работы

1. Построить приближение таблично заданной функции по методу наименьших квадратов многочленами 0-ой, 1-ой и 2-ой степеней.

X	-2	-1
Y	9.9	5.1	1.9	1.1	1.9

Построить графики функции и найденных многочленов.

2. Функция y=a/x+b задана таблицей своих значений.

x	0.1	0.2	0.5
y	10.22	5.14	2.76

Найти параметры a и b по методу наименьших квадратов.

Указание. Предварительно свести задачу к линейной, сделав замену: t=1/x. Тогда функция y приближается многочленом 1-ой степени a t+b.

3. Вывести нормальную систему уравнений для определения параметров a, b, c функции g(x)=a sin(x)+b cos(x)+c, осуществляющей среднеквадратичную аппроксимацию таблично заданной функции y(x).

Вопросы

1. Сформулируйте постановку задачи приближения функции по методу наименьших квадратов.

2. Что такое среднеквадратичное отклонение.

3. Как определить степень приближающего многочлена.

4. Из какого условия выводится нормальная система наименьших квадратов.

Интерполяция функций

Вопросы

1. Сформулируйте постановку задачи приближения функции по методу интерполяции.

2. Запишите интерполяционный многочлен Ньютона и интерполяционный многочлен Лагранжа первой степени.

3. Сформулируйте теорему об оценке погрешности интерполяции.

4. Какие преимущества имеет запись интерполяционного многочлена по формуле Ньютона перед формулой Лагранжа.

10 Интерполяция сплайнами

Интерполяция сплайнами

Пусть отрезок [a,b] разбит точками на n частичных отрезков . Сплайном степени m называется функция , обладающая следующими свойствами:

1) функция непрерывна на отрезке [a,b] вместе со своими производными до некоторого порядка p;

2) на каждом частичном отрезке функция совпадает с некоторым алгебраическим многочленом степени m.

Разность m-p между степенью сплайна и наивысшим порядком непрерывной на отрезке [a ,b] производной называют дефектом сплайна. Кусочно-линейная функция является сплайном первой степени с дефектом, равным единице. Действительно, на отрезке [a ,b] сама функция (нулевая производная) непрерывна. В то же время на каждом частичном отрезке совпадает с некоторым многочленом первой степени.

ПРИМЕР 3. Построение параболического сплайна.

Пусть дан фрагмент таблицы значений функции:

x	-1
y	1.5	0.5	2.5

Требуется построить параболический сплайн дефекта 1.

Так как строится сплайн , то он будет представлен двумя полиномами 2-ой степени:

.

Функция должна удовлетворять условиям:

- это есть условие интерполяции;

- это есть условие непрерывности первой производной.

Таким образом, получили 5 условий для нахождения 6-сти неизвестных. Два условия дополнительно накладывают на сплайн в граничных точках.

Возьмем, например дополнительное граничное условие следующего вида .

Тогда получим систему уравнений относительно неизвестных коэффициентов :

Эта система легко решается:

, , , , , .

Таким образом:

.

Наиболее широкое распространение получили сплайны 3 степени (кубические сплайны) с дефектом равным 1 или 2. Система для осуществления сплайн-интерполяции кубическими полиномами предусматривает несколько встроенных функций. Одна из них рассмотрена в примере.

ПРИМЕР 4 . Построение сплайн-интерполяции (рис. 10.4).

% Построить интерполяцию сплайнами функции Рунге

% Введём функцию Рунге

f = inline('1./(1+25*x.^2)');

% Вычислим таблицу значений

x = linspace(-1, 1, 10);

y = f(x);

% Вычислим сплайн-интерполяцию

xx = linspace(-1, 1, 100);

yy = spline(x, y, xx);

% Начертим графики

axes('NextPlot', 'Add');

plot(x, y, 'LineWidth', 2);

% Красным на графике - аппроксимация, жирным - исходная функция.

plot(xx, yy, 'Color', 'r');

Рис. 10.4 - построение сплайн-интерполяции

Погрешность приближения кубическими сплайнами.

Пусть функция f имеет на отрезке [a,b] непрерывную производную четвертого порядка и .

Тогда для интерполяционного кубического сплайна справедлива оценка погрешности: .

Задание для самостоятельной работы

1. Функция y = f(x) задана таблицей своих значений.

X		0.2	0.4	0.6	0.8
Y	0.75	1.1	1.35	1.25	1.05	0.8

Предложить способы интерполирования для нахождения значений функции в точках 0.24, 0.5, 0.96.

2. Функция y = f(x) задана таблицей своих значений.

X
Y

Построить интерполяционный кубический сплайн с граничными условиями , .

3. Проинтерполировать функцию задачи 2 методом кусочно-линейной интерполяции и построить график исходной функции и найденных многочленов.

Вопросы

1. Объясните разницу между глобальной и кусочно-полиномиальной интерполяцией. Почему на практике чаще используется кусочно-полиномиальная интерполяция.

2. Дайте определение интерполяционного сплайна m-ой степени.

3. Что такое дефект сплайна.

4. Запишите формулу сплайна первой степени с дефектом единица.

Численное дифференцирование

Производная функции есть предел отношения приращения функции к приращению независимой переменной при стремлении к нулю приращения независимой переменной:

.

При численном нахождении производной заменим отношение бесконечно малых приращений функций и аргумента отношением конечных разностей. Очевидно, что чем меньше будет приращение аргумента, тем точнее численное значение производной.

Численное интегрирование

Определенным интегралом функции f(x), взятом в интервале от a до b, называется предел, к которому стремится интегральная сумма при стремлении всех промежутков ∆x_i к нулю:

.

При приближенном вычислении определенного интеграла шаг интегрирования h=∆x выбирается конечным: , где I_i - элемент интегральной суммы. Заменяя подынтегральную функцию на каждом шаге отрезками линий нулевого, первого и второго порядков, получаем приближенные формулы для вычисления интеграла методами прямоугольников, трапеций и Симпсона соответственно.

1. Приближенные формулы для вычисления интеграла методом прямоугольников (рис 12.1).

Рис. 12.1 - вычисление интеграла методом прямоугольников

Правило прямоугольников (n=0). Заменяем график функции F(x) горизонтальной линией (линий нулевого порядка) и вычисляем значение элемента интегральной суммы как площадь прямоугольника

, где h - шаг интегрирования, у₀ - значение функции в точке х=х₀

у(х₀)=у₀

2. Приближенные формулы для вычисления интеграла методом трапеций (рис. 12.2).

Рис. 12.2. - вычисление интеграла методом трапеций

Правило трапеций (n=1). Заменяем график функции F(x) прямой, проходящей через две точки (х₀,у₀) и (х₀+h,у₁), и вычисляем значение элемента интегральной суммы как площадь трапеции

3. Приближенные формулы для вычисления интеграла методом Симпсона (рис. 12.3).

Рис. 12.3. - вычисление интеграла методом Симпсона

Правило Симпсона (n=2). Заменяем график функции F(x) квадратичной параболой, проходящей через три точки с координатами (х₀,у₀), (х₀+h,у₁), (х₀+2h,у₂). Расчетную формулу для вычисления элемента интегральной суммы получим, используя интерполяционный многочлен Лагранжа, в виде: y(x)=y₀A₀(x)+y₁A₁(x)+y₂A₂(x), где:

При x₀=0; x₁=h; x₂=2h, получим:

При интегрировании на отрезке [a,b] расчетные формулы для методов прямоугольника, трапеций и Симпсона имеют вид:

,

где h - шаг по x, f_a, f_i, f_b - значения функции при x равном a, x_i, b соответственно.

Для метода прямоугольников приведены две расчетные формулы, так как площадь прямоугольника на каждом шаге интегрирования может определяться по левой или правой стороне. Суть метода прямоугольников для отрезка [a, b] проиллюстрирована на рисунке, при этом площадь под кривой f(x) (вспомните геометрический смысл определенного интеграла) заменена суммой площадей заштрихованных прямоугольников (рис. 12.4).

Рис. 12.4 - суть метода прямоугольников для отрезка [a, b]

Задание для самостоятельной работы

1. Вычислить значение определенного интеграла аналитически и численно четырьмя методами для пяти значений N, где N – число разбиений интервала интегрирования N=10; 20; 50; 100; 1000. Результаты расчета вывести на экран и распечатать в виде таблицы. Представление результатов расчета:

N	Аналит. Значение	Метод прямоуг. 1	Метод прямоуг. 2	Метод трапеций	Метод Симпсона

2. Построить графики функций I=F(N).

Варианты интегралов приведены в таблице:

Вар.	Вид интеграла	Вар.	Вид интеграла

Модифик