Дискретное распределение. Числовые характеристики.

1. Производятся три независимых опыта, в каждом из которых событие А появляется с вероятностью 0,4. Рассматривается случайная величина Х – число появлений события А в трех опытах. Найти функцию распределения случайной величины Х и построить ее график. Найти ее математическое ожидание, дисперсию, среднее квадратическое отклонение.

2. Рабочий у конвейера при сборке механизм устанавливает в него определенную деталь. В некоторых случаях деталь приходится подгонять и проверять качество подгонки пробной установкой ее в механизм. Закон распределения числа пробных установок детали Х задается таблицей:

xi
p(xi)	0,38	0,26	0,20	0,14	0,02

Определить математическое ожидание и дисперсию рассматриваемой случайной величины. Найти функцию распределения случайной величины Х и построить ее график.

3. В лотерее на каждые 100 билетов приходится 15 выигрышных. Количество и размер выигрышей даны в таблице:

Размер выигрыша
Количество выигрышей

1) найти ряд распределения случайного выигрыша на один лотерейный билет; 2) определить математическое ожидание и дисперсию рассматриваемой случайной величины; 3) найти функцию распределения и построить ее график.

4. В результате систематических испытаний мотков оцинкованной проволоки диаметром 0,6 мм, предназначенной для изготовления канатов, установлено теоретическое распределение по прочностям:

Разрывное усилие
Вероятность	0,04	0,02	0,07	0,18	0,27	0,29	0,03	0,06	0,04

Найти математическое ожидание разрывного усилия проволоки (СВ Х) и математическое ожидание разрывного усилия 60 проволок, из которых будет свит канат. Найти дисперсию СВ Х, функцию распределения и построить ее график.

5. Число a-частиц, достигающих счетчика в некотором опыте, является случайной величиной, распределенной по следующему закону:

a
p(a)	0,021	0,081	0,156	0,210	0,195	0,151	0,097	0,054	0,026	0,011	0,007

Найти математическое ожидание и дисперсию числа частиц, достигающих счетчика. Найти вероятность того, что число частиц, достигших счетчика, будет не меньше 4. Найти функцию распределения и построить ее график.

6. В лотерее разыгрывается мотоцикл стоимостью 250 руб., велосипед стоимостью 50руб. и часы ценой 40 руб. Найти математическое ожидание выигрыша для лица, имеющего один билет, если общее число билетов равно 100. Найти дисперсию выигрыша. Найти функцию распределения и построить ее график.

7. Из урны, содержащей 3 белых и 4 черных шара, извлекается по одному шару без возвращения до первого появления белого шара. Найти математическое ожидание числа выгнутых шаров и дисперсию. Найти функцию распределения и построить ее график.

8. В результате испытаний двух приборов (А и В) установлена вероятность наблюдения помех, оцениваемых по трехбалльной системе:

Уровень помех
Вероятность наблюдения помех данного уровня	Прибор А	0,40	0,35	0,25
Прибор В	0,35	0,45	0,20

По приведенным данным выбрать лучший прибор, если лучшим является тот, который в среднем имеет меньший уровень помех. Для прибора А найти также дисперсию уровня помех, функцию распределения и построить ее график.

9. Испытуемый прибор состоит из четырех элементов. Вероятность отказа для элемента с номером i равна p_i = 0,2+0,1 (i-1). Определить математическое ожидание и дисперсию числа отказавших элементов, если отказы элементов независимы. Найти дисперсию и функцию распределения, построить ее график.

10. Автоматическая линия при нормальной настройке может выпускать бракованное изделие с вероятностью р. Переналадка линии производится сразу после первого же бракованного изделия. Найти среднее число всех изделий, изготовленных между двумя переналадками линии, и дисперсию.

11. Вероятность приема позывного сигнала одной радиостанции другой радиостанцией равна 0,2 при каждой посылке. Позывные подаются каждые 5 с до тех пор, пока не будет получен ответный сигнал. Общее время прохождения позывного и ответного сигналов равно 16с. Найти среднее число подаваемых позывных сигналов до установления двусторонней связи и дисперсию.

12. Независимые испытания аппаратуры повторяются до тех пор, пока она не даст отказ. Вероятность отказа от испытания к испытанию не меняется и равна р. Найти математическое ожидание и дисперсию числа безотказных испытаний.

13. Дискретная случайная величина Х принимает три возможных значения: x₁=4 с вероятностью p₁=0,5, x₂=6 с вероятностью p₂=0,3, x₃ с вероятностью p₃. Зная, что М(Х) = 8, найти x₃, p₃ и дисперсию данной величины. Найдите функцию распределения и постройте ее график.

14. В партии из 10 деталей содержится три нестандартных. Наудачу отобраны две детали. Найти математическое ожидание и дисперсию числа нестандартных деталей среди двух отобранных. Найдите функцию распределения и постройте ее график.

15. Среди поступивших в ремонт 10 часов 6 шт. нуждаются в общей чистке механизма. Часы не рассортированы по виду ремонта. Мастер, желая найти часы, нуждающиеся в общей чистке механизма, рассматривает их поочередно и, найдя такие часы, прекращает дальнейший просмотр. Найти математическое ожидание количества просмотренных часов, дисперсию, функцию распределения и постройте ее график.

16. При установившемся технологическом процессе 2/3 всей производимой продукции станок-автомат выпускает первым сортом и 1/3 — вторым. Найти математическое ожидание и дисперсию числа изделий первого сорта среди 5 изделий, отобранных случайным образом. Найдите функцию распределения и постройте ее график.

17. Производятся 4 выстрела с вероятностями попадания в цель р₁=0,6; р₂=0,4; р₃=0,5; р₄=0,7. Найти математическое ожидание и дисперсию общего числа попаданий.

18. В результате систематической проверки качества валиков, изготовляемых на отрегулированном автоматическом станке, было установлено следующее теоретическое распределение их по диаметру:

Диаметр валиков в мм	9,77	9,78	9,79	9,80	9,81	9,82
Вероятность	0,05	0,09	0,18	0,32	0,21	0,15

Найти математическое ожидание и дисперсию диаметра валиков, изготовляемых на отрегулированном станке. Найдите функцию распределения и постройте ее график.

19. Монету бросают до первого выпадения герба. Найти математическое ожидание и дисперсию числа бросаний монеты.

20. Две игральные кости бросают 5 раз подряд. Найти математическое ожидание и дисперсию числа бросаний, при которых на каждой из 2 костей появляется нечетное число очков. Найдите функцию распределения и постройте ее график.

21. В лотерее продано 100 билетов стоимостью 10 руб. каждый. Разыгрывается 4 денежных приза в 1000, 500, 200 и 50 руб. Каково математическое ожидание и дисперсия чистого выигрыша человека, купившего два билета? Найдите функцию распределения и постройте ее график.

22. Четыре одинаковые электрические лампочки временно выворачивают из патронов и кладут в ящик. Затем их случайным образом вынимают из него и вворачивают в патроны. Каково математическое ожидание и дисперсия числа лампочек, попавших в тот патрон, из которого они были вывернуты? Найдите функцию распределения и постройте ее график.

23. Найти математическое ожидание и дисперсию суммы очков, выпавших при одновременном бросании двух игральных костей.

24. Выборка, состоящая из четырех шаров, производится из урны, содержащей три красных и пять белых шаров. Если в выборке не менее двух красных шаров, то игрок получает один доллар; в противном случае он теряет 50 центов. Каково математического ожидание и дисперсия выигрыша этого игрока? Найдите функцию распределения и постройте ее график.

25. Возможные значения случайной величины Х являются натуральные числа 1, 2, 3, …,10, и P(X=k)=ck, где с есть некоторая константа. Найдите с, математическое ожидание МХ и дисперсию.

26. Найти математическое ожидание и дисперсию числа делителей Х произвольного наугад выбранного натурального числа, заключающегося в пределах от 1 до 10. Найдите функцию распределения и постройте ее график.

27. Закон распределения случайной величины Х имеет вид

Х	x1	x2	x3
Р	0,5	0,3	0,2

Найти x₁, x₂, x₃, если известно, что они представляют возрастающую арифметическую прогрессию, а МХ = 1,7, DX = 0,61. Найдите функцию распределения и постройте ее график.

28. Дискретная случайная величина Х может принимать только два значения: x₁ и x₂ (x₁<x₂). Найти закон распределения случайной величины Х, если известны вероятность p₁=0,2 возможного значения x₁, математическое ожидание МХ = 3,8 и дисперсия DX = 0,16. Найдите функцию распределения и постройте ее график.

29. Испытывается устройство, состоящее их трех независимых приборов, вероятности отказа которых 0,3; 0,5 и 0,6. Найти математическое ожидание и дисперсию СВ Х — числа отказавших приборов. Найдите функцию распределения и постройте ее график.

30. Обрыв связи произошел на одном из пяти звеньев телефонного кабеля. Монтер последовательно проверяет звенья для обнаружения места разрыва, вероятность обрыва связи для всех звеньев одинакова. Найти математическое ожидание и дисперсию СВ Х — числа обследованных звеньев. Найдите функцию распределения и постройте ее график.

Задача 10.

Функция распределения

1. Функция распределения величины Х имеет вид

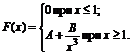
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(0<X<3).

2. Функция распределения величины Х имеет вид

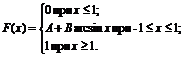
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(-1<X<0).

3. Функция распределения величины Х имеет вид

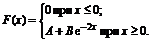
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(1<X<3).

4. Функция распределения величины Х имеет вид

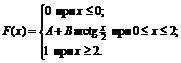
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(-1<X<1).

5. Функция распределения величины Х имеет вид

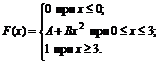
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(1<X<4).

6. Функция распределения величины Х имеет вид

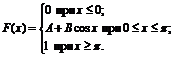
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(-1<X<1).

7. Функция распределения величины Х имеет вид

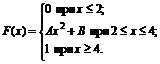
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(1<X<3).

8. Функция распределения величины Х имеет вид

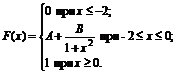
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(-1<X<0).

9. Функция распределения величины Х имеет вид

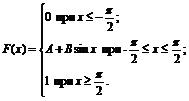
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(0<X<p/4).

10. Функция распределения величины Х имеет вид

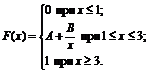
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(2<X<5).

11. Функция распределения величины Х имеет вид

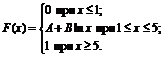
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(2<X<4).

12. Функция распределения величины Х имеет вид

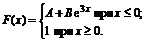
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(-1<X<1).

13. Функция распределения величины Х имеет вид

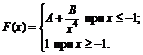
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(-2<X<0).

14. Функция распределения величины Х имеет вид

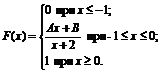
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(-3<X<3).

15. Функция распределения величины Х имеет вид

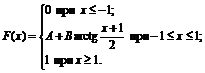
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(0<X<3).

16. Функция распределения величины Х имеет вид

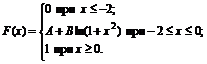
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(-1<X<1).

17. Функция распределения величины Х имеет вид

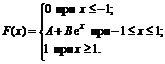
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(0<X<2).

18. Функция распределения величины Х имеет вид

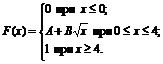
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(1<X<6).

19. Функция распределения величины Х имеет вид

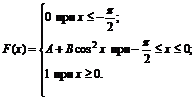
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(-p/4<X<p/4).

20. Функция распределения величины Х имеет вид

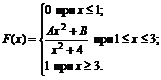
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(0<X<2).

21. Функция распределения величины Х имеет вид

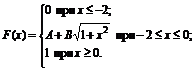
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), s(X); 4) вероятность P(-1<X<1).

22. Функция распределения величины Х имеет вид

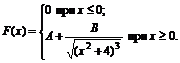
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(-2<X<1).

23. Функция распределения величины Х имеет вид

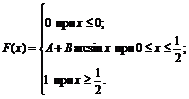
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(-1<X<1/4).

24. Функция распределения величины Х имеет вид

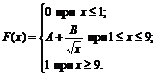
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(0<X<4).

25. Функция распределения величины Х имеет вид

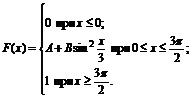
Найти: 1) значение параметров А и В; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(-p/2<X<p/2).

26. Функция распределения величины Х имеет вид

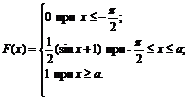
Найти: 1) значение параметра а; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(-p/4<X<0).

27. Функция распределения величины Х имеет вид

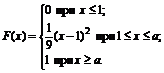
Найти: 1) значение параметра а; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(2<X<3).

28. Функция распределения величины Х имеет вид

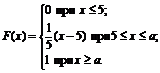
Найти: 1) значение параметра а; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(6<X<7).

29. Функция распределения величины Х имеет вид

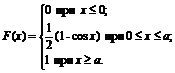
Найти: 1) значение параметра а; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(p/4<X<p/3).

30. Функция распределения величины Х имеет вид

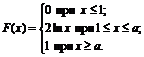
Найти: 1) значение параметра а; 2) плотность вероятностей f(x); 3) M(X), D(X), s(X); 4) вероятность P(1<X<1,5).

Задача 11.

Функция плотности

1. Плотность вероятностей величины Х имеет вид

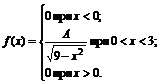
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

2. Плотность вероятностей величины Х имеет вид

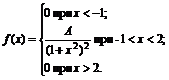
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

3. Плотность вероятностей величины Х имеет вид

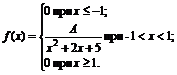
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

4. Плотность вероятностей величины Х имеет вид

Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

5. Плотность вероятностей величины Х имеет вид

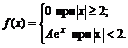
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

6. Плотность вероятностей величины Х имеет вид

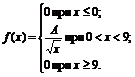
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

7. Плотность вероятностей величины Х имеет вид

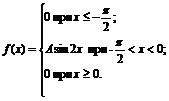
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

8. Плотность вероятностей величины Х имеет вид

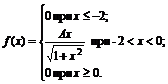
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

9. Плотность вероятностей величины Х имеет вид

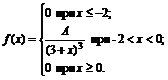
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

10. Плотность вероятностей величины Х имеет вид

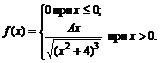
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

11. Плотность вероятностей величины Х имеет вид

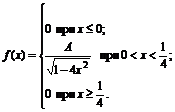
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

12. Плотность вероятностей величины Х имеет вид

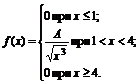
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

13. Плотность вероятностей величины Х имеет вид

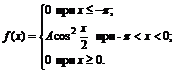
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

14. Плотность вероятностей величины Х имеет вид

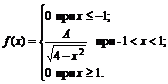
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

15. Плотность вероятностей величины Х имеет вид

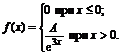
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

16. Плотность вероятностей величины Х имеет вид

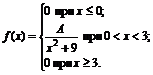
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

17. Плотность вероятностей величины Х имеет вид

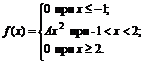
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

18. Плотность вероятностей величины Х имеет вид

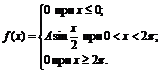
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

19. Плотность вероятностей величины Х имеет вид

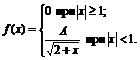
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

20. Плотность вероятностей величины Х имеет вид

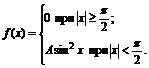
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

21. Плотность вероятностей величины Х имеет вид

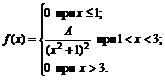
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

22. Плотность вероятностей величины Х имеет вид

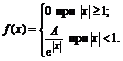
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

23. Плотность вероятностей величины Х имеет вид

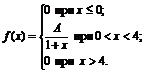
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

24. Плотность вероятностей величины Х имеет вид

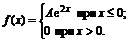
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

25. Плотность вероятностей величины Х имеет вид

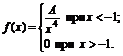
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

26. Плотность вероятностей величины Х имеет вид

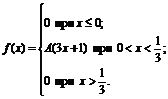
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

27. Плотность вероятностей величины Х имеет вид

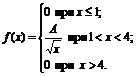
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

28. Плотность вероятностей величины Х имеет вид

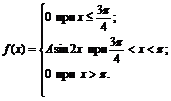
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

29. Плотность вероятностей величины Х имеет вид

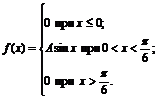
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

30. Плотность вероятностей величины Х имеет вид

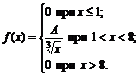
Найти: 1) значение параметра А; 2) функцию распределения F(x); 3) построить графики f(x) и F(x).

Задача 12.