Типовой расчет по высшей математике
Самарский государственный
университет путей сообщения
Типовой расчет по высшей математике

для студентов очной формы обучения
всех специальностей
Cамара – 2007
УДК 519.2
Теория вероятностей:Типовой расчет по высшей математике/ Л.В. Кайдалова; Самара: СамГАПС, 2007. 57 с.
Утверждена на заседании кафедры протокол № от
Печатается по решению редакционно-издательского совета университета
Методические указания составлены в соответствии с Государственным образовательным стандартом, с действующей программой по высшей математике для технических специальностей.
В пособии приведены индивидуальные задания и методические указания по теории вероятностей. Приведены необходимые для решения задач таблицы.
Предназначено для студентов 2-ого курса всех специальностей очной формы обучения.
Ил. 3. Библиогр.: 5 назв.
Составитель Л.В. Кайдалова, к. ф.-м. н.
Рецензенты: д. ф.-м. н., проф. СамГТУ Радченко В.П.,
к. ф.-м. н., доцент Миронов Ф.С.
Ó Кайдалова Л.В.
Ó Самарский государственный университет путей сообщения, 2007
Основные обозначения и сокращения
Р(А) – вероятность события А;
Х – случайная величина;
х – значение случайной величины X;
СВ – случайная величина;
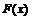 – функция распределения СВ X;
– функция распределения СВ X;
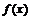 – функция плотности СВ X;
– функция плотности СВ X;
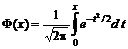 – функция Лапласа;
– функция Лапласа;
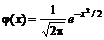 – функции плотности нормированного нормального распределения;
– функции плотности нормированного нормального распределения;
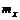 = M(x) – математическое ожидание СВ Х;
= M(x) – математическое ожидание СВ Х;
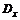 = D(x) – дисперсия СВ Х;
= D(x) – дисперсия СВ Х;
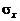 – среднее квадратическое отклонение СВ Х;
– среднее квадратическое отклонение СВ Х;
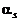 – вероятностный начальный момент порядка s;
– вероятностный начальный момент порядка s;
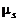 – вероятностный центральный момент порядка s;
– вероятностный центральный момент порядка s;
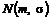 – одномерное нормальное распределение с математическим ожиданием m и средним квадратическим отклонением
– одномерное нормальное распределение с математическим ожиданием m и средним квадратическим отклонением 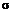 .
.
Порядок выполнения и защиты типового расчета по высшей математике
1. Выполнение учебного задания проводится по графику, устанавливаемому кафедрой высшей математики.
2. Решения задач необходимо представлять в письменном виде. Нумерация задач должна совпадать с их нумерацией в учебном задании.
3. Во время защиты студент должен уметь отвечать па теоретические вопросы, пояснять решения примеров из задания, решать примеры аналогичного типа.
4. Студенты, не отчитавшиеся по типовому расчету, не допускаются к сдаче экзамена по курсу.
5. При выполнении типового расчета необходимо соблюдать следующие правила:
ü на обложке тетради указать Ф.И.О., название предмета, номер группы, номер варианта, например,
Самарский государственный университет путей сообщений
Кафедра «Высшая математика»
Типовой расчет № 1
по теории вероятностей
вариант № 3
студента 1881 гр.
Иванова Сергея Николаевича
Проверил доцент Кузнецов В.П.
Cамара – 2009
ü представлять решения задач последовательно со всеми развернутыми расчетами и краткими пояснениями;
ü рисунки выполнять карандашом с использованием чертежного инструмента;
ü проверять правильность решения задач.
Задание № 1
Алгебра событий
1.1.а). На сортировочной станции работают 15 сменных инженеров, из них 3 – женщины. В смену занято 3 человека. Найти вероятность того, что в случайно выбранную смену мужчин окажется не менее 2.
б). Рабочий обслуживает 4 станка. Вероятность того, что в течение часа первый станок не потребует внимания рабочего, равна 0,7, для второго станка эта вероятность равна 0,8, для третьего – 0,9 и, наконец, для четвертого – 0,85. Найти вероятность того, что в течение часа по крайней мере один станок потребует к себе внимания рабочего.
в). Пассажир может обратиться за получением билета в одну из трех касс. Вероятности обращения в каждую кассу зависят от их местоположения и равны соответственно р1, р2, р3. Вероятность того, что к моменту прихода пассажира имеющиеся в кассе билеты будут распроданы, равна для первой кассы Р1, для второй – Р2, для третьей – Р3. Пассажир направился за билетом в одну из касс и приобрел билет. Найти вероятность того, что это была первая касса.
1.2. а). Для производственной практики на 30 студентов предоставлено 15 мест в Абдулино, 8 – в Кузнецке, и 7 – в Ртищеве. Какова вероятность того, что два определенных студента попадут на практику в определенный город?
б). Устройство содержит два узла. Работа каждого узла необходима для работы устройства в целом. Вероятность выхода из строя первого узла равна 0,02, второго – 0,03. Найти вероятность выхода из строя устройства в целом.
в). У рыбака имеется три излюбленных места для ловли рыбы, которые он посещает с равной вероятностью каждое. Если он закидывает удочку на первом месте, рыба клюет с вероятностью р1; на втором – с вероятностью р2; на третьем – с вероятностью р3. Известно, что рыбак, выйдя на ловлю рыбы, три раза закинул удочку, и рыба клюнула только один раз. Найти вероятность того, что он удил на первом месте.
1.3. а). Производственная фирма изготавливает вагоны; каждый вагон имеет дефекты с вероятностью р. Вагон осматривается одним контролером; он обнаруживает имеющиеся дефекты с вероятностью р1, а если дефекты не обнаружены, пропускает изделие в готовую продукцию. Кроме того, контролер может по ошибке забраковать вагон, не имеющий дефектов; вероятность этого равна a. Найти вероятности следующих событий: А – вагон будет забракован; В – вагон будет забракован, но ошибочно; С – вагон будет пропущен в готовую продукцию с дефектами.
б). Рабочий обслуживает 3 станка. Вероятность того, что в течение часа станок не потребует внимания рабочего, равна для первого станка 0,7, для второго – 0,8, для третьего – 0,85. Найти эту вероятность при следующих условиях: 1) в течение часа ни один из станков не потребует внимания рабочего; 2) все станки потребуют внимания рабочего.
в). Группа студентов состоит из а отличников, b – хорошо успевающих и с – занимающихся слабо. Отличники на предстоящем экзамене могут получить только отличные оценки. Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки. Слабо занимающиеся могут получить с равной вероятностью хорошие, удовлетворительные и неудовлетворительные оценки. Для сдачи экзаменов вызывается наугад один студент. Найти вероятность того, что он получит хорошую или отличную оценку.
1.4. а). Производственная фирма в среднем дает 21 % продукции высшего сорта и 70 % продукции первого сорта. Найти вероятность того, что случайно взятое изделие окажется первого или высшего сорта.
б). Человеку, достигшему 60–летнего возраста, вероятность умереть на 61–м году жизни в определенных условиях равна 0,09. Какова в этих условиях вероятность того, что из трех человек в возрасте 60 лет: 1) все трое будут живы через год; 2) по крайней мере один из них будет жив?
в). Для некоторой местности среднее число ясных дней в июле равно 24. Найти вероятность того, что первые три дня в июле будут ясными.
1.5. а). Каждый из трех пассажиров с равной вероятностью может сесть в любой из 10 вагонов электропоезда. Найти вероятность того, что все трое попадут: 1) в разные вагоны; 2) в один вагон.
б). Завод изготавливает определенного типа детали; каждая деталь имеет дефект с вероятностью 0,05. Деталь осматривается одним контролером; он обнаруживает имеющийся дефект с вероятностью 0,97, а если дефект не обнаружен, пропускает деталь в готовую продукцию. Кроме того, контролер может по ошибке забраковать деталь, не имеющую дефекта; вероятность этого равна 0,01. Найти вероятности следующих событий: А – деталь будет забракована; В – деталь будет забракована, но ошибочно; С – деталь будет пропущена в готовую продукцию с дефектом.
в). Изделие проверяется на стандартность одним из трех товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0,25, ко второму – 0,26 и к третьему – 0,49. Вероятность того, что изделие будет признано стандартным первым товароведом, равна 0,95, вторым – 0,98, третьим – 0,97. Найти вероятность того, что стандартное изделие проверено вторым контролером.
1.6. а). В магазин поступают лампочки, изготовленные на трех заводах. С первого завода поступают 50 % всех лампочек, со второго – 30 % и с третьего – 20 %. Среди лампочек, изготовленных первым заводом, 80 % – первого сорта, в продукции второго завода лампочки первого сорта составляют 70 %, а в продукции третьего завода – 60 %. Какова вероятность того, что купленная в магазине лампочка окажется первого сорта?
б). На сборку поступают изделия из четырех цехов. Вероятности брака в каждом из цехов соответственно равны 0,04; 0,03; 0,06; 0,02. Первый цех поставляет 30 изделий, второй – 20, третий – 50, четвертый – 25. На сборку поступило бракованное изделие. Какова вероятность, что это изделие из второго цеха?
в). Пусть вероятность искажения при передаче одного сообщения по телеграфу постоянна и равна 0,05. После скольких передач с вероятностью, не меньшей 0,75, появится хотя бы одно искаженное сообщение?
1.7. а). Детали, изготовленные цехом завода, попадают для проверки на стандартность к одному из двух контролеров. Вероятность того, что деталь попадет к первому контролеру, равна 0,6; а ко второму – 0,4. Вероятность того, что деталь будет признана стандартной первым контролером, равна 0,94, а вторым – 0,98. Деталь при проверке была признана стандартной. Найти вероятность того, что эту деталь проверил первый контролер.
б).Деталь с вероятностью 0,01 имеет дефект a, с вероятностью 0,02 – дефект b и с вероятностью 0,005 – оба дефекта. Найти вероятность того, что деталь имеет хотя бы один дефект.
в). Два регулятора контролируют работу двигателя. За время работы при наличии двух регуляторов двигатель отказывает с вероятностью 0,1, при работе одного из них – 0,2, второго – 0,15, а при отказе обоих регуляторов – 0,3. Первый регулятор имеет надежность 0,9, второй – 0,8. Все элементы выходят из строя независимо друг от друга. Найти вероятность того, что двигатель выйдет из строя.
1.8. а). Два автомата производят детали, которые поступают на общий конвейер. Вероятность получения нестандартной детали на первом автомате равна 0,06, а на втором – 0,09. Производительность второго автомата вдвое больше, чем первого. С конвейера взята нестандартная деталь. Найти вероятность того, что эта деталь произведена вторым автоматом.
б). Устройство содержит два узла. Работа каждого узла необходима для работы устройства в целом. Вероятность выхода из строя первого узла равна 0,01, второго – 0,03. Найти вероятность выхода из строя устройства в целом.
в). Сборщик получил 3 ящика деталей: в первом ящике 40 деталей, из них 20 с дефектом; во втором – 50, из них 10 с дефектом; в третьем – 30 деталей, из них 15 с дефектом. Найти вероятность того, что деталь, извлеченная из наудачу взятого ящика, окажется с дефектом.
1.9. а). Испытывается прибор, состоящий из двух узлов, надежности которых 0,8 и 0,9. Узлы отказывают независимо друг от друга. Прибор отказал. Найти с учетом этого вероятности гипотез: а) неисправен только первый узел; б) неисправен только второй узел; в). неисправны оба узла.
б).При поступлении очередной партии деталей рабочему необходимо переналаживать станок с вероятностью 0,2. Найти вероятность того, что первые пять партий деталей не потребуют переналадки.
в). На заводе болты изготовляются на трех станках, которые производят соответственно 25, 30 и 45 % всего количества болтов. В продукции станков брак составляет соответственно 4, 3 и 2 %. Какова вероятность, что болт, случайно взятый из поступившей продукции, окажется дефектным?
1.10. а). Рабочий обслуживает три станка. Вероятность того, что в течение смены потребуется переналаживать первый станок, равна 0,7, второй – 0,75, третий – 0,8. Найти вероятность того, что в течение смены рабочий переналадит два станка.
б).Электронная схема принадлежит одной из трех партий с вероятностями 0,25; 0,5 и 0,25. Вероятность того, что схема проработает сверх гарантированного срока службы для каждой из партий, составляет 0,1; 0,2 и 0,4. Найти вероятность того, что наугад взятая схема проработает сверх гарантийного срока службы.
в). Прибор содержит два блока, исправность каждого из которых необходима для функционирования прибора. Вероятности безотказной работы для этих блоков соответственно равны 0,99 и 0,97. Прибор вышел из строя. Определить вероятность того, что отказали оба блока.
1.11. а). 15 экзаменационных билетов содержат по 2 вопроса, которые не повторяются. Студент может ответить только на 25 вопросов. Определить вероятность того, что экзамен будет сдан, если для этого необходимо ответить либо на два вопроса билета, либо на один вопрос доставшегося билета и на указанный вопрос другого билета.
б). На склад поступает продукция трех фабрик, причем продукция первой фабрики составляет 20 %, второй – 16 %, третьей – 34 %. Известно также, что среднее количество нестандартных изделий для первой фабрики составляет 5 %, для второй – 2 %, для третьей – 1 %. Найти вероятность того, что взятое наудачу изделие окажется стандартным.
в). Две перфораторщицы набрали по одинаковому пакету перфокарт. Вероятность того, что первая перфораторщица допустит ошибку, равна 0,05; вторая – 0,1. При сверке перфокарт была обнаружена ошибка, найти вероятность того, что первая перфораторщица ошиблась.
1.12. а). На складе телевизионного ателье имеется 70 % кинескопов, изготовленных заводом № 1; остальные кинескопы изготовлены заводом № 2. Вероятность того, что кинескоп не выйдет из строя в течение гарантийного срока службы, равна 0,8 для кинескопов завода № 1 и 0,7 для кинескопов завода № 2. Кинескоп выдержал гарантийный срок службы. Найти вероятность того, что он изготовлен заводом № 2.
б). Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор, равна 0,95; второй – 0,9. Найти вероятность того, что при аварии сработает только один сигнализатор, и вероятность срабатывания хотя бы одного сигнализатора.
в). На сборку поступают детали с трех автоматов. Известно, что 1-й автомат дает 0,3 % брака, 2-й – 0,2 %, 3-й – 0,4 %. Найти вероятность поступления на сборку бракованной детали, если с 1-ого автомата поступили 1000, со 2-ого – 2000, с 3-его – 2500 деталей.
1.13.а). На двух станках производятся одинаковые детали. Вероятность того, что деталь, произведенная на первом станке, будет стандартной, равна 0,8, а на втором – 0,9. Производительность второго станка втрое больше производительности первого. Найти вероятность того, что стандартной будет деталь, взятая наудачу с транспортера, на который поступают детали с обоих станков.
б). Устройство состоит из трех независимо работающих элементов. Вероятность выхода из строя первого элемента равна 0,2; второго – 0,1; третьего – 0,3. Устройство выйдет из строя, если откажут, по крайней мере, два элемента. Найти вероятность выхода из строя устройства.
в). Вероятность того, что студент сдаст первый экзамен, равна 0,9; вероятность сдачи второго экзамена – 0,85; а третьего – 0,8. Найти вероятность того, что хотя бы два экзамена будут сданы.
1.14. а). В отдел технического контроля поступили 3000 деталей с первого станка и 2000 со второго. Первый станок в среднем дает 0,2 % брака, а второй – 0,3 %. Найти вероятность того, что первая деталь продукции окажется бракованной.
б). На склад поступает продукция трех фабрик, причем продукция первой фабрики составляет 20 %, второй – 46 % и третьей – 34 %. Известно также, что средний процент нестандартных изделий для первой фабрики равен 5 %, для второй – 2 % и для третьей – 1 %. Найти вероятность того, что наудачу взятое изделие произведено на первой фабрике, если оно оказалось стандартным.
в). Радиолокационная станция ведет наблюдение за тремя объектами. За время наблюдения первый объект может быть потерян с вероятностью 0,3, второй и третий – с вероятностями 0,4. Найти вероятность того, что ни один объект не потерян.
1.15. а). Рабочий обслуживает 4 станка. Вероятность того, что в течение смены станок будет работать бесперебойно, равна для первого станка 0,9; для второго – 0,85; для третьего – 0,8 и для четвертого – 0,75. Какова вероятность того, что в течение одной смены хотя бы один станок потребует наладки?
б).На склад поступают однотипные подшипники. Первый завод поставляет 80 % всего количества, второй – 20 %. Известно, что первый завод выпускает 90 % продукции, способной прослужить положенный срок, а второй – 95 %. Какова вероятность того, что наугад взятый подшипник прослужит положенный срок?
в). Изделие проходит три этапа контроля по различным независимым параметрам. Вероятность того, что оно будет отбраковано на первом этапе, равна 0,02, на втором – 0,03, на третьем – 0,02. Найти вероятность того, что изделие будет небракованным после контроля.
1.16. а). Известно, что в партии из 600 лампочек 200 лампочек изготовлены на первом заводе, 250 – на втором и 150 – на третьем. Известны вероятности 0,97; 0,91 и 0,93 того, что лампочка окажется стандартной при изготовлении ее соответственно на первом, втором и третьем заводах. Какова вероятность того, что наудачу выбранная из данной партии лампочка, окажется стандартной?
б).Три станка работают независимо друг от друга. Вероятность того, что первый станок в течение смены выйдет из строя, равна 0,1; для второго и третьего станков эти вероятности соответственно равны 0,2 и 0,3. Найти вероятность того, что в течение смены хотя бы один станок выйдет из строя.
в). На склад готовой продукции поступает 80 % изделий из первого цеха и 20 % из второго. Продукция первого цеха имеет 1 % брака, второго – 2 % брака. Найти вероятность того, что наугад взятое со склада изделие, оказавшееся бракованным, поступило из первого цеха.
1.17. а). С первого автомата на сборку поступают 20 % деталей, со второго – 30 %, с третьего – 50 %. Первый автомат дает в среднем 0,2 % брака, второй – 0,3 %, третий – 1 %. Найти вероятность того, что деталь поступила со второго автомата, если известно, что она бракованная.
б).По мишени производится три выстрела с вероятностью попадания при каждом выстреле 0,8. Найти вероятность событий: 1) все 3 промаха; 2) попадание в мишень не раньше, чем при третьем выстреле.
в). На заводе детали изготовляются на трех станках, производящих соответственно 25, 30 и 45 % всего количества деталей. В продукции станков брак составляет соответственно 4, 3 и 2 %. Какова вероятность того, что деталь, случайно взятая из всей продукции, окажется годной?
1.18. а). Руководитель компании решил воспользоваться услугами двух из трех транспортных фирм. Вероятности несвоевременной доставки груза для первой, второй, и третьей фирм равны соответственно 0,05, 0,1, и 0,07. Сопоставив эти данные с данными о безопасности грузоперевозок, руководитель пришел к выводу о равнозначности выбора, и решил сделать его по жребию. Найти вероятность того, что отправленный груз, будет доставлен своевременно.
б).Устройство содержит 2 независимо работающих блока. Вероятности отказа блоков соответственно равны 0,05 и 0,08. Найти вероятность отказа устройства, если для этого достаточно, чтобы отказал хотя бы один блок.
в). Имеется пять компьютеров модели Pentium Pro и семь – модели Pentium III. Вероятность того, что за время работы не откажет Pentium Pro, равна 0,99; а Pentium III – 0,95. Производится расчет на произвольно выбранной машине. Машина отказала. Найти вероятность того, что отказал компьютер модели Pentium Pro.
1.19. а). В сборочный цех поступают детали с трех автоматов. Первый автомат дает 3 % брака, второй – 1 % и третий – 2 %. Определить вероятность попадания на сборку небракованной детали, если с каждого автомата поступило соответственно 500, 200, 300 деталей.
б).При одном цикле обзора радиолокационной станции, следящей за космическим объектом, последний объект обнаруживается с вероятностью p. Обнаружение объекта в каждом цикле происходит независимо от других. Найти вероятность того, что при n циклах объект будет обнаружен.
в). Прибор содержит два блока, исправность каждого из которых необходима для функционирования прибора. Вероятности безотказной работы для этих блоков соответственно равны 0,99 и 0,97. Прибор вышел из строя. Определить вероятности того, что отказал второй блок.
1.20. а). Работа дизеля контролируется двумя регуляторами. При наличии обоих регуляторов дизель отказывает с вероятностью q12, при работе одного из них – с вероятностью q1; при работе другого – с вероятностью q2, при отказе обоих регуляторов – с вероятностью q0. Первый регулятор имеет надежность р1, второй – р2. Все элементы выходят из строя независимо друг от друга. Найти полную вероятность безотказной работы дизеля.
б). На склад поступает продукция трех фирм. Причем продукция первой фирмы составляет 20 %, второй – 46 % и третьей – 34 %. Известно также, что средний процент нестандартных изделий для первой фирмы равен 5 %, для второй – 2 % и для третьей – 1 %. Найти вероятность того, что наудачу взятое изделие произведено второй фирмой, если оно оказалось стандартным.
в). Брак в продукции завода вследствие дефекта a составляет 5 %, причем среди забракованных по признаку a продукции в 10 % случаев встречается дефект b, а в продукции, свободной от дефекта a дефект b встречается в 1 % случаев. Найти вероятность встречи дефекта b во всей продукции.
1.21. а). Работа двигателя контролируется двумя регуляторами. При наличии обоих регуляторов двигатель отказывает с вероятностью 0,99, при работе одного из них – с вероятностью 0,95; при работе другого – с вероятностью 0,97, при отказе обоих регуляторов – с вероятностью 0,5. Первый регулятор имеет надежность 0,9, второй – 0,8. Все элементы выходят из строя независимо друг от друга. Найти полную вероятность безотказной работы двигателя.
б). Две перфораторщицы набили по одинаковому пакету перфокарт. Вероятность того, что первая перфораторщица допустит ошибку, равна 0,03; вторая – 0,01. При сверке перфокарт была обнаружена ошибка, найти вероятность того, что вторая перфораторщица ошиблась.
в). Компания по страхованию автомобилей делит водителей на категории: А – те, кто мало рискует; В – рискует умеренно; С – рискует сильно. Известно, что 30 % всех водителей принадлежит к категории А, 50 % – к категории В и 20 % – к категории С. Вероятности попасть в аварию в течение года для водителей названных категорий соответственно равны 0,01; 0,03; 0,1. Наудачу выбранный водитель попал в течение года в аварию. Какова вероятность, что он относится к категории А?
1.22. а). На складе телевизионного ателье имеются 70 % кинескопов, изготовленных заводом № 1, остальные кинескопы изготовлены заводом № 2. Вероятности того, что кинескоп не выйдет из строя в течение гарантийного срока службы, равны 0,8 для кинескопов завода № 1, 0,7 – для кинескопов завода № 2. Найти вероятность того, что наудачу взятый кинескоп выдержит гарантийный срок службы.
б). Рабочий обслуживает четыре станка. Вероятность того, что в течение первого часа первый станок не потребует внимания рабочего, равна 0,3, второй – 0,4, третий – 0,7, четвертый – 0,4. Найти вероятность того, что в течение часа ни один станок не потребует внимания рабочего.
в). В первой бригаде 5 рабочих имеют стаж от одного до трех лет, 7 рабочих – от трех до пяти лет и 4 рабочих – свыше пяти лет. Во второй бригаде 6 рабочих имеют стаж от одного до трех лет, 3 рабочих – от трех до пяти лет и 5 рабочих – свыше пяти лет. Из первой бригады во вторую переведен один рабочий. Найти вероятность того, что наудачу взятый из нового состава второй бригады рабочий имеет стаж менее пяти лет.
1.23. а). В транспортной фирме имеется 10 новых автомобилей и 5 старых, которые ранее находились в ремонте. Вероятность исправной работы в течение недели для нового автомобиля равна 0,94, старого – 0,91. Найти вероятность того, что наудачу заказанный автомобиль будет исправно работать в течение недели.
б). В мастерской имеются два мотора. При существующем режиме работы вероятность того, что мотор работает с полной нагрузкой, равна 0,4. Определить вероятность того, что оба мотора работают с полной нагрузкой.
в). Процесс изготовления изделия включает три этапа. На первом этапе возможен брак с вероятностью 0,01, на втором – с вероятностью 0,04, на третьем – 0,03. Найти вероятность того, что после изготовления изделия оно не будет бракованным.
1.24. а). Детали, необходимые для сборки прибора, поступают с двух автоматов, производительность которых одинакова. Вычислить вероятность поступления на сборку стандартной детали, если один из автоматов дает в среднем 3 % нарушения стандарта, а второй – 2 %.
б).На предприятии при массовом изготовлении изделий брак составляет в среднем 2,4 % от общего количества всех изделий. Из числа годных 92,3 % составляют изделия 1 сорта. Какова вероятность того, что наудачу взятое изделие, окажется 1 сорта?
в). Устройство содержит два узла. Работа каждого узла необходима для работы устройства в целом. Вероятность выхода из строя первого узла равна 0,01, второго – 0,03. Вышел из строя один из узлов. Какова вероятность того, что вышел из строя первый узел?
1.25. а). На сборку поступают однотипные изделия из четырех цехов. Вероятности брака в каждом из цехов соответственно равны 0,04; 0,03; 0,06 и 0,02. Первый цех поставляет 30, второй – 20, третий – 50 и четвертый – 25 изделий. На сборку поступило бракованное изделие. Какова вероятность, что это изделие поступило на сборку из третьего цеха?
б).Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сработает первый сигнализатор, равна 0,95; второй – 0,9. Найти вероятность того, что при аварии сработает только один сигнализатор.
в). У сборщика имеется 20 деталей: 6 изготовлены заводом № 1, 10 – заводом № 2 г. Москвы, 4 – заводом г. Санкт–Петербурга. Наудачу взяты 2 детали. Найти вероятность того, что хотя бы одна из них окажется изготовленной в Москве.
1.26. а). Рабочий обслуживает три станка, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0,02, для второго – 0,03, для третьего – 0,04. Обрабатываемые детали складываются в один контейнер. Производительность первого станка в 3 раза больше, чем второго, а третьего в 2 раза меньше, чем второго. Определить вероятность того, что взятая наудачу деталь, обработана на третьем станке, если она оказалась бракованной.
б).Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором и третьем справочниках, соответственно равны 0,6; 0,7 и 0,8. Найти вероятность того, что формула содержится только в одном справочнике.
в). Руководитель компании решил воспользоваться услугами трех транспортных фирм. Вероятности несвоевременной доставки груза для первой, второй и третьей фирм равны соответственно 0,2, 0,3 и 1 %. Первая фирма может обеспечить компанию 20 % машин, вторая – 30 %, третья – 50 %. Найти вероятность того, что отправленный груз будет доставлен своевременно.
1.27. а). Два датчика посылают сигналы в общий канал связи, причем первый из них посылает вдвое больше сигналов, чем второй. Вероятность получить искаженный сигнал от первого датчика равна 0,01, от второго – 0,03. Какова вероятность получить искаженный сигнал в общем канале связи?
б).Имеется пять партий деталей: три партии по 8 штук, из которых 6 стандартных и 2 нестандартных, и две партии по 10 штук, из которых 7 стандартных и 3 нестандартных. Наудачу берется одна из партий, а из этой партии выбирается наугад деталь. Определить вероятность того, что взятая деталь будет стандартной.
в). Сборщик получает в среднем 50 % деталей первого завода, 30 % – второго завода, 20 % – третьего завода. Вероятность того, что деталь первого завода отличного качества, равна 0,7; для деталей второго и третьего заводов соответственно 0,8 и 0,9. Наудачу взятая деталь оказалась отличного качества. Найти вероятность того, что деталь изготовлена первым заводом.
1.28. а).Устройство состоит из трех независимо работающих элементов. Вероятность выхода из строя первого элемента равна 0,02, второго – 0,01, третьего – 0,3. Устройство выйдет из строя, если откажет хотя бы один элемент. Найти вероятность выхода из строя устройства.
б). На складе телевизионного ателье имеется 70 % кинескопов, изготовленных заводом №1; остальные кинескопы изготовлены заводом №2. Вероятность того, что кинескоп не выйдет из строя в течение гарантийного срока службы, равна 0,8 для кинескопа завода № 1 и 0,7 для кинескопа завода № 2. Найти вероятность того, что кинескоп, выдержавший гарантийный срок, изготовлен заводом №1.
в). На сборку поступают однотипные изделия из четырех цехов. Вероятности брака в каждом из цехов соответственно равны 0,04; 0,03; 0,06 и 0,02. Первый цех поставляет 30, второй – 20, третий – 50 и четвертый – 25 изделий. Найти вероятность того, что взятое на удачу изделие окажется небракованным.
1.29. а). Батарея из трех орудий производит залп по цели. Вероятность попадания в цель первым, вторым и третьим орудиями соответственно равны 0,7; 0,8; 0,9. Найти вероятность того, что цель будет поражена хотя бы одним попаданием.
б). Два автомата производят детали, которые поступают на общий конвейер. Вероятность получения нестандартной детали на первом автомате равна 0,06, а на втором – 0,09. Производительность второго автомата вдвое больше, чем первого. С конвейера взята нестандартная деталь. Найти вероятность того, что эта деталь произведена на первом автомате.
в). Локомотив может работать в двух режимах: нормальном и аварийном. Нормальный режим наблюдается в 95 % всех случаев, аварийный – в 5 %. Вероятность выхода из строя локомотива за время t в нормальном режиме 0,1, а в аварийном – 0,7. Найти полную вероятность выхода из строя локомотива за время t.
1.30. а). В двух ящиках содержится по 15 деталей, причем в первом ящике стандартных деталей 9, а во втором – 10. Из первого ящика наудачу извлечена деталь и переложена во второй ящик. Найти вероятность того, что извлеченная после этого также наудачу деталь из второго ящика будет стандартной.
б). Электронное устройство содержит шесть блоков, один из которых отказал. С целью устранения неисправности последовательно проверяют блоки и при необходимости заменяют исправным. Какова вероятность нахождения неисправности в первом, во втором, в третьем, в четвертом, в пятом, в шестом блоках?
в). При поиске неисправности в вычислительном устройстве последовательно проверяются его блоки. Вероятность неисправности первого блока равна 0,2, второго – 0,3, третьего – 0,4. События, состоящие в выходе из строя блоков, независимы. Найти вероятность того, что при проверке указанных трех блоков неисправность будет обнаружена.
Задание № 2
Задание № 3
Методические указания
Алгебра событий
Перестановки (множество n элементов отличающихся только порядком): 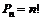
Сочетания из n элементов по m (множество элементов, составленные из n различных элементов по m, которые отличаются хотя бы одним элементом): 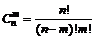 ,
, 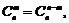
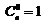 .
.
Размещения (множество элементов, составленные из n различных элементов по m, которые отличаются либо составом, либо порядком):
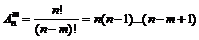 .
.
Гипергеометрическая вероятность: 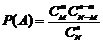 .
.
Формула сложения вероятностей:
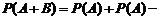
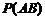 .
.
Формула умножения вероятностей:
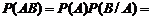
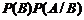 .
.
Для независимых событий 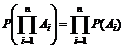 .
.
По крайней мере одно из независимых событий 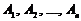 произойдет:
произойдет: 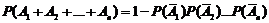 .
.
Формула полной вероятности: 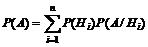 .
.
Формула Байеса: 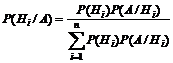 .
. 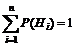 .
.
2 Пример 1. В урне содержится 5 белых и 6 черных шаров. Из урны случайно вынимаются 2 шара. Найти вероятность того, что оба шара будут белыми.
Решение. Общее число исходов 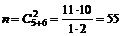 . Число благоприятных исходов
. Число благоприятных исходов 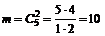 . Вероятность события А = {оба шара белые} равна Р(А) =
. Вероятность события А = {оба шара белые} равна Р(А) = 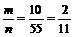 . v
. v
2 Пример 2. По мишени производится 3 выстрела. Пусть Аi = {попадание при i-ом выстреле, 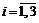 }. Представить в виде сумм, произведений или сумм произведений
}. Представить в виде сумм, произведений или сумм произведений 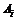 и
и 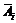 следующие события: А = {все три попадания}; В = {все три промаха}; С = {хотя бы одно попадание}; D = {хотя бы один промах}; Е = {не меньше двух попаданий}; F = {не больше одного попадания}; G = {попадание в мишень не раньше, чем при третьем выстреле}.
следующие события: А = {все три попадания}; В = {все три промаха}; С = {хотя бы одно попадание}; D = {хотя бы один промах}; Е = {не меньше двух попаданий}; F = {не больше одного попадания}; G = {попадание в мишень не раньше, чем при третьем выстреле}.
Решение. Данные события можно представить в виде следующих комбинаций: 1) 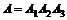 ; 2)
; 2) 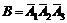 ; 3)
; 3) 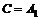 + A2 + A3 или
+ A2 + A3 или 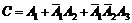 или
или 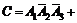
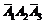
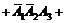
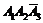
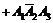
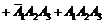 ; 4) D =
; 4) D = 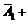
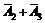 ; 5) E =
; 5) E =