Упрощение ОЧУС картами Вейча

Функция P (Карта Карно)

Y1 y2 h G t45QwRU9rIv7u1xnxo30icM+VIJDyGdaQR1Cl0npyxqt9jPXIbF2cr3Vgde+kqbXI4fbViZRtJRW N8Qfat3htsbyvL9YBe+jHjfz+HXYnU/b688h/fjexajU48O0eQERcAr/ZvjDZ3QomOnoLmS8aBWk S64S+B4/g2B9kcx5OCpI0sUKZJHL2wbFLwAAAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4AAADh AQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAAIQA4 /SH/1gAAAJQBAAALAAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAAIQDJ p6cgggIAALYGAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAIAAAA IQBBjF7H4QAAAAkBAAAPAAAAAAAAAAAAAAAAANwEAABkcnMvZG93bnJldi54bWxQSwUGAAAAAAQA BADzAAAA6gUAAAAA "> P x1 x2
					*	*
					*	*
					*	*
					*	*
	*	*	*	*	*	*	*
	*	*	*	*	*	*	*
	*	*	*	*	*	*	*
	*	*	*	*	*	*	*

Функция Q1 (Карта Карно)

Y1 y2 h P x1 x2
000					*	*
					*	*
					*	*
					*	*
	*	*	*	*	*	*	*
	*	*	*	*	*	*	*
	*	*	*	*	*	*	*
	*	*	*	*	*	*	*

Функция Q2 (Карта Карно)

(в дальнейшем будет упрощаться алгоритмом рота)

Y1 y2 h P x1 x2					110
000					*	*
					*	*
					*	*
					*	*
	*	*	*	*	*	*	*
	*	*	*	*	*	*	*
	*	*	*	*	*	*	*
	*	*	*	*	*	*	*

Безразличные наборы

Y1 y2 h P x1 x2
000					*	*
					*	*
					*	*
					*	*
	*	*	*	*	*	*	*
	*	*	*	*	*	*	*
	*	*	*	*	*	*	*
	*	*	*	*	*	*	*

Результата минимизации ОЧУС с помощью карт Вейча и алгоритма рота

ОЧУС функция P

ОЧУС функция Q1

+ + + + + +

ОЧУС функция Q2

+ + +

Безразличные наборыОЧУС (Для алгоритма Рота)

+ +

Реализация ОЧУС в заданном базисе

базис: А

&

4

ОЧУС функция P

Результат:

ОЧУС функция Q1

Результат:

ОЧУС функция Q2

+ + +

Результат:

Реализация переключательной функции Q1 и P

Реализация переключательной функции Q2

Логический синтез преобразователя множителя (ПМ)

Преобразователь множителя (ПМ) служит для исключения из множителя диад 11, заменяя их на триады и диад 10, заменяя их на триады .

Таблица истинности ПМ.

Вх. диада	Мл. бит	Зн.	Вых. диада
Qn	Qn-1	Qn-2	P	S1	S2

Qn-1Qn-2

Минимизируем выходные функции

Qn

P

P = Q_n

Видно, что S₁минимизировать нельзя, поэтому .

Qn

Qn-1Qn-2

S2

Логический синтез одноразрядного четверичного сумматора на основе мультиплексоров

Мультиплексор – это логическая схема, имеющая n информационных входов, m управляющих входов и один выход. При этом должно выполняться условие n = 2^m.На выход мультиплексора может быть пропущен без изменений любой (один) логический сигнал, поступающий на информационные входы. Порядковый номер информационного входа, значение с которого в данный момент должно быть передано на выход, определяется двоичным кодом на управляющих входах.

Для синтеза ОЧС будем использовать мультиплексор “один из восьми” (1 из 8ми).

Входы I₀,I₁,…, I₇ - это информационные входы мультиплексора. Сигналы х₁ могут принимать значения 0 или 1. Входы S₀ ,S₁ , S₂ - управляющие входы.

Таблица истинности для ОЧС на мультиплексорах

a1a2b1	b2p	П	Псхема	S1	S1схема	S2	S2схема
			b2p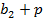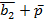
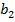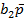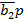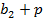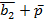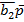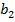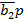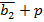			Const 0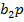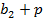
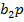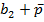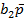			Const 1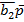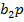

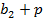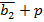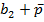Оценка эффективности минимизации и подсчёт времени

ОЧУС:

До минимизации :

C_P=4+4*6+4=32;

C_Q1=6+12*6+12=90;

C_Q2=6+12*6+12=90;

C₁= C_P+ C_Q1+ C_Q2= 32+90+90 = 212;

После минимизации:

C_P= 2+3_или-не = 5;

C_Q1= 5+4_или-не *2+3_или-не *1+2_или-не *2+1= 21;

C_Q2= 6+5_или-не *1+3_или-не *2+2_или-не *2+1 = 22;

C₂= C_P+ C_Q1+ C_Q2= 5+21+22 = 48;

Эффективность минимизации θ=С₁/C₂;

θ = 212/48 = 4,42; Цена схемы уменьшилась в 4,42 раза.

ОЧС:

C_П=5*16+16+5=101;

C_S1=5*16+16+5=101;

C_S2=5*16+16+5=101;

C₁= C_П+ C_S1+ C_S2=101+101+101=303;

После минимизации:

C_П = 2+2_и*1+3_и*6+7_или +7+1=37

C_S1=5+4_и*8+8_или +8+1= 49;

C_S2=5+4_и*8+8_или +8+1= 49;

C₂=C_П+ C_S1+ C_S2=37+49+49 = 135;

Эффективность минимизации θ=С₁/C₂;

θ = 303/135= 2,24; Цена схемы уменьшилась в 2,24 раза.