Интерполяция при постоянном шаге

Конечной разностью функции y=f(x) c шагом Dx =h называют функцию Dy=f(x+h)-f(x). Это первая конечная разность. Вторая конечная разность D²y=D(Dy)=[f(x+2h)-f(x+h)]-[f(x+h)-f(x)]=f(x+2h)-2f(x+h)+f(x) и т.д.

Предположим, что функция y=f(x) задана в виде таблицы из четырех точек. Построим для нее таблицу конечных разностей:

i

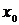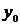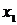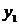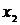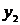В этой таблице

Предположим, что шаг в этой таблице – постоянный, то есть

(3.4)

Полином, проходящий через все точки таблицы (а это будет полином степени не выше третьей):

Здесь .

Запишем общий вид полинома n-й степени:

( 3.6 )

“I “ означает, что это первый интерполяционный полином Ньютона. Он удобен для вычислений, когда точка х=х^*, в которой нужно вычислить функцию, расположена ближе к началу таблицы.

Если точка х^* расположена ближе к концу таблицы, то удобнее пользоваться формулой второго интерполяционного полинома Ньютона:

( 3.7 )

Результаты применения формул (3.6) и (3.7) – одни и те же, если используются одни и те же узлы таблицы.

Покажем, как можно построить таблицу конечных разностей на Scilab.

clc

x=[0 2 4 6];y=[5 12 27 33];dy=diff(y),dy2=diff(y,2),dy3=diff(y,3)

disp('Таблица конечных разностей функции у')

dy =

7. 15. 6.

dy2 =

8. - 9.

dy3 =

- 17.

Таблица конечных разностей функции у

Обратная интерполяция

Постановка задачи:

Функция y задана в виде таблицы

x	x0	x1	…	xn
y	y0	y1	…	yn

Требуется найти значение аргумента x^*, при котором функция принимает некоторое значение y^*.

Задачу можно решить по крайней мере двумя различными способами.

1. а) Строим интерполяционный полином (как правило, ИПЛ)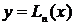

в) Решаем уравнение 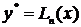любым подходящим численным методом (например, методом деления отрезка пополам).

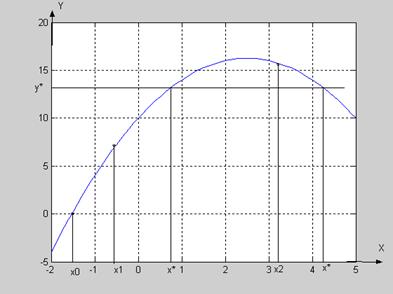
Из рисунка видно, что задача может иметь не единственное решение.

2. а) Строим интерполяционный полином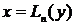

в) Подставляем в этот полином значение y^* и получаем x^*:

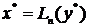( 3.8 )

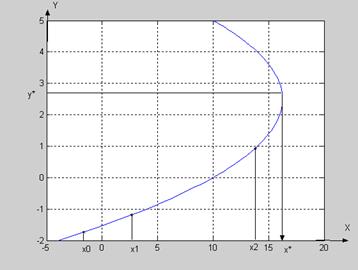
Как правило, решения задачи, полученные первым и вторым способом, будут различными.

Численное дифференцирование

Численное дифференцирование – это вычисление производных от функций, заданных в виде таблицы. Задача решается в два этапа. На первом этапе строится интерполяционный полином. На втором этапе находятся производные (первая, вторая и т.д.) от этого полинома.

Если шаг постоянный, то на первом этапе строят ИПН.

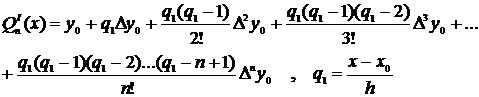
Найдем первую производную от этого полинома.

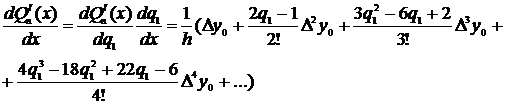( 3.9 )

Аналогично,

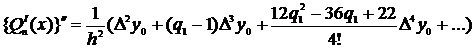( 3.10 )

Если производную нужно вычислить в каком-либо узле таблицы (например, в точке х=х₀), то формулы (3.9) и (3.10) упрощаются, так как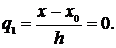

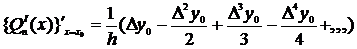( 3.11 )

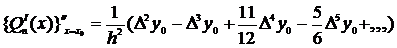( 3.12 )

Задача численного дифференцирования относится к числу некорректных задач. Это означает, что сколь угодно малые погрешности в исходных данных могут привести к большим погрешностям результата решения, поэтому к численному дифференцированию не следует прибегать без особой необходимости. По тем же причинам обычно не вычисляют производные старших порядков.

Нахождение значения производной в заданной точке на Scilab:

Найти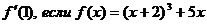

clc

function y=f(x)

y=(x+2).^3+5*x;

endfunction

numdiff(f,1)

ans =

32.