Меры погрешности аппроксимации

Мерой погрешности назовем некоторое неотрицательное число m(f,Q). Естественно потребовать, чтобы m(f,Q)=0, если f(x) и Q(x,c_j) совпадают на общем для их задания множестве значений аргументов. Справедливо и обратное утверждение.

После того, как мера каким-либо образом задана, необходимо указать способ получения коэффициентов с_j. Для поиска коэффициентов можно воспользоваться минимаксным подходом, который осуществляет равномерное приближение функций, методом наименьших модулей, методом наименьших квадратов и другими.

Метод наименьших квадратов

Чаще всего при точечной аппроксимации используют меру

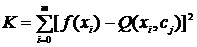(2.2)

а коэффициенты с_j ищут из условия

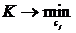(2.3)

Это точечная квадратичная аппроксимация.

При интегральной аппроксимации

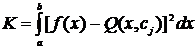
Описанный подход к задаче аппроксимации называется методом наименьших квадратов. Условия (2.2) и (2.3) геометрически означают: из всех кривых заданного вида выбирают ту, у которой сумма площадей квадратов отклонений – наименьшая.

В математике кривую y=Q(x,c_j) называют регрессией Y на X . Это означает, что у функции y=Q(x,c_j) число искомых коэффициентов меньше количества узлов, в крайнем случае возможно равенство

n+1£m+1 (2.4)

Если аргументом считать y, а x – функцией, то говорят о регрессии X на Y. Отклонения в этом случае откладывают по оси X.

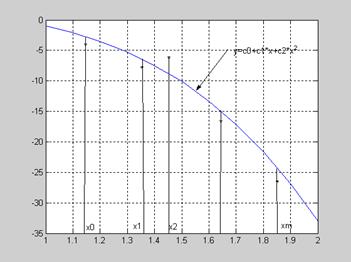
Регрессия Y на X

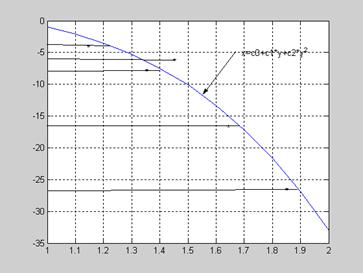
Регрессия X на Y

2.2 Нахождение коэффициентов c_j при точечной аппроксимации методом наименьших квадратов

Минимальное значение K в формуле (2.2) достигается при тех с_j , при которых

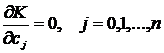(2.5)

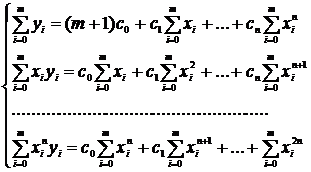(2.6)

Здесь x_i и y_i – заданные числа.

Пример: построить аппроксимирующую параболу для функции

x
y	-1,2	-0,1	1,3	1,8

Составим таблицу

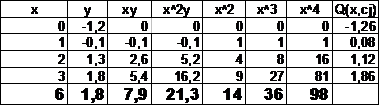
Запишем систему нормальных уравнений для нашей кривой.

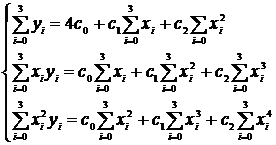или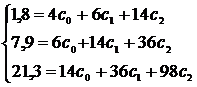

Решая систему, получаем:

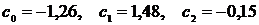или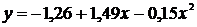

Вычисляя K по формуле (2.9), получаем: K=0,0720. У любой параболы второй степени значение K, вычисленное по формуле (2.9), будет больше, чем 0,0720.

Неполиномиальная регрессия

Часто на практике возникает следующая задача. Имеется объект исследования (ОИ), который характеризуется набором переменных: входных ( 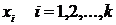) и выходной y.

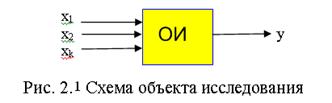
Требуется найти зависимость выходной переменной от входных

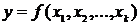( 2.7 )

При этом считается, что механизмы процессов, протекающих внутри объекта исследования, неизвестны, а имеются только соответствующие значения входных и выходных параметров. Такая задача носит название задачи «черного ящика».

Рассмотрим простейший случай, когда на вход действует только одна переменная x и требуется найти

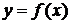( 2.8 )

Решение задачи моделирования в этом случае состоит из 4 этапов:

1) проведение эксперимента

2) выбор вида экспериментальной зависимости

3) нахождение параметров выбранной зависимости

4) исследование модели и выводы.

На первом этапе задаем значения входной переменной x из возможного диапазона и замеряем соответствующие значения выходной переменной y.

x	x0	x1	…	xm
y	y0	y1	…	ym

По экспериментальным данным строим график

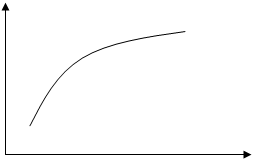Рис. 2.2 Экспериментальная кривая

На втором этапе необходимо выбрать формулу, которая могла бы описать экспериментальные данные. Во втором столбце таблицы 2.1 приведены основные типовые формулы, наиболее часто встречающиеся в задачах химии и химической технологии.

Таблица 2.1

№	Формула	Средние точки

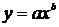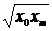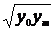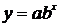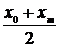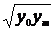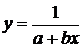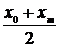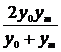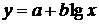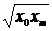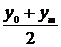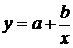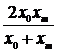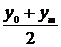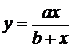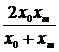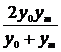Здесь х₀, y₀ – первая, а х_m , y_m – последняя точки исходной таблицы.

Для каждой функции рассчитывается средняя точка. Все эти точки наносятся на график с экспериментальной кривой.

Выбирается та кривая, средняя точка которой находится ближе всего к экспериментальной кривой. Покажем, как решается эта часть задачи на конкретном примере.

Пусть x=[5 7 9 11 13];y=[2.5 4.9 8 12.1 16.9];

Тогда

xap =(5+13)/2=9

xgео =(5*13)^0.5= 8.06

xgar =2*5*13/(5+13)= 7.22

yap =(2.5+16.9)/2= 9.7

ygeo = (2.5*16.9)^0.5= 6.5

ygar = 2*2.5*16.9/(2.5+16.9)= 4.36

Средняя точка для первой кривой –(8.06, 6.5)

Средняя точка для второй кривой –(9, 6.5)

Средняя точка для третьей кривой –(9, 4.36)

Средняя точка для четвертой кривой –(8.06, 9.7)

Средняя точка для пятой кривой –(7.22, 9.7)

Средняя точка для шестой кривой –(7.22, 4.36)

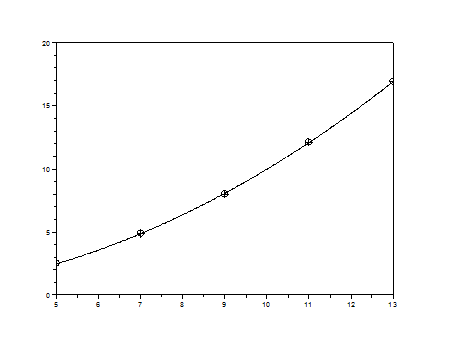
Нанесем на график исходные данные (х и у) и соединим соседние точки отрезками прямых. На этот же график нанесем средние точки для каждой кривой, снабдив их соответствующими номерами.

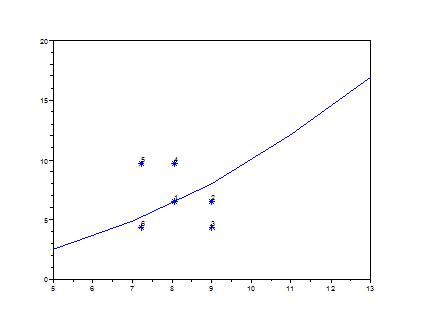
Эту часть задачи можно решить, построив график на Scilab.

clc

xbasc()

x=[5 7 9 11 13];y=[2.5 4.9 8 12.1 16.9];

n=length(x);

xap=(x(1)+x(n))/2

xgar=2*x(1)*x(n)/(x(1)+x(n))

xgeo=(x(1)*x(n))^.5

yap=(y(1)+y(n))/2

ygar=2*y(1)*y(n)/(y(1)+y(n))

ygeo=(y(1)*y(n))^.5

t=[xgeo xap xap xgeo xgar xgar]

z=[ygeo ygeo ygar yap yap ygar]

plot(x,y)

plot(t,z,'*')

for i=1:6

xnumb(t(i),z(i),i)

end

Из графика видно, что ближе всего к экспериментальной кривой лежит точка с номером 1, поэтому таблично заданную функцию будем заменять первой кривой .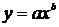

Приведем полученную кривую к линейному виду.

Кривую 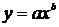(как и любую другую из таблицы 2.1) приводят к линейному виду (то есть к виду 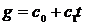) заменой переменных. 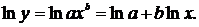В этом случае g=lny, c₀=lna, c₁=b, t=lnx.

Коэффициенты (параметры) с₀ и с₁ находят методом наименьших квадратов, то есть добиваются того, чтобы 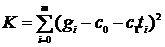было минимальным. Эта задача сводится к решению системы нормальных уравнений:

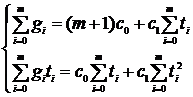или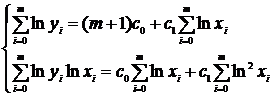

В нашем примере получается система:

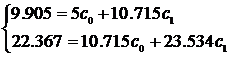
Решая ее, получаем с₀=- 2.294 с₁= 1.995

Зная с₀ и с₁ , находят a и b. В нашем примере

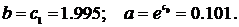
Таким образом, мы заменили таблично заданную функцию кривой .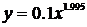

Подставляя в полученную формулу с конкретными значениями a и b значения x₀, x₁, … , x_m и сравнивая их с исходными данными, делают выводы об адекватности математической модели.

В нашем случае модель получилась адекватной.

x	y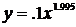
	2.5	2.480
	4.9	4.853
		8.011
	12.1	11.956
	16.9	16.685

Решим эту часть задачи на scilab.

Решение.

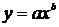. Покажем, как найти неизвестные коэффициенты a и b на Scilab.

clc

xbasc()

function [zr]=F(c,z)

zr=z(2)-(c(1)*z(1)^c(2))

endfunction

x=[5 7 9 11 13];

y=[2.5 4.9 8 12.1 16.9];

z=[x;y];

c=[1;1];

[d,S]=datafit(F,z,c)

t=5:.01:13;

Yt=(d(1)*t^d(2));

plot2d(x,y,-3);

plot2d(t,Yt);

S = 0.0067979

d = 0.0973802 2.0102774

В ответе d(1)= 0.0973802 это a, d(2)= 2.0102774 это b.

Таким образом, уравнение кривой, полученной на scilab,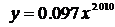

x	y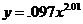
	2.5	2.464
	4.9	4.846
		8.032
	12.1	12.022
	16.9	16.819

Тема 3. Интерполяция

Интерполяция – частный случай аппроксимации, когда аппроксимирующая кривая проходит через все точки таблицы, то есть

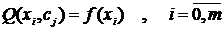(3.1)

Задача интерполяции ставится так:

Функция y=f(x) задана в виде таблицы

x	x0	x1	…	xm
y	y0	y1	…	ym

Требуется вычислить значение функции в точке x, не совпадающей ни с одним из узлов таблицы. Если эта точка лежит между узлами, то такая задача называется интерполяцией. Если точка x лежит за пределами таблицы, то говорят о задаче экстраполяции.

Очевидно, что коэффициенты с_j можно найти методом наименьших квадратов, положив n=m.

Рассмотрим другие способы решения этой задачи.

Интерполяция по Лагранжу

Построим полином

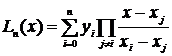(3.2)

Выражение (3.2) – алгебраический полином степени n. Покажем, что он проходит через все точки таблицы при n=2 и n=3.

; ; ;

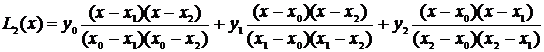
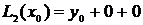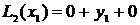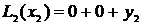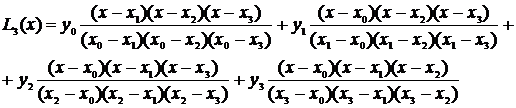
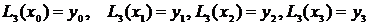
Выражение (3.2) – интерполяционный полином Лагранжа, проходящий через все точки таблицы. Теперь, чтобы найти значение функции в некоторой точке x^* , которой нет в таблице, достаточно подставить эту точку вместо x в формулу (3.2) и считать, что

y^*=L_n(x^*) (3.3)