Тема 1. Численные методы решения уравнений

Тема 1. Численные методы решения уравнений

Уравнение называется алгебраическим, если его можно представить в виде:

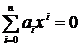(1.1)

Формула (1.1) – каноническая форма записи алгебраического уравнения. Если уравнение 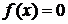не удается привести к виду (1.1) заменой переменных, то уравнение называется трансцендентным.

Решить уравнение означает найти такие значения x, при которых уравнение превращается в тождество.

Известно, что уравнение (1.1) имеет ровно n корней – вещественных или комплексных. Если n=1, 2, 3 [и иногда 4 (биквадратное уравнение], то существуют точные методы решения уравнения (1.1). Если же n>4 или уравнение – трансцендентное, то таких методов не существует, и решение уравнения ищут приближенными методами. Всюду при дальнейшем изложении будем предполагать, что f(x) – непрерывная функция. Методы, которые мы рассмотрим, пригодны для поиска некратных (то есть изолированных) корней.

Отделение корня

Решение уравнения состоит из двух этапов: 1 – отделение корня, 2 – его уточнение.

Отделить корень – значит указать такой отрезок [a, b] , на котором содержится ровно один корень уравнения .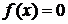

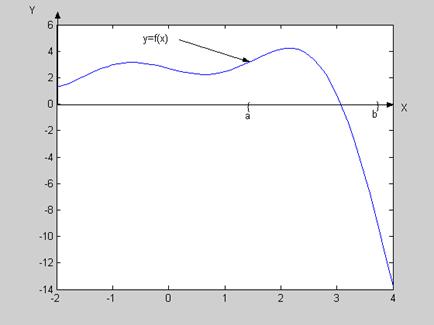
Не существует алгоритмов отделения корня, пригодных для любых функций f(x). Если удастся подобрать такие a и b, что

1) f(a) f(b)<0 (1.2)

2) f( x) – непрерывная на [a, b] функция (1.3)

3) f( x) – монотонная на [a, b] функция (1.4)

то можно утверждать, что на отрезке [a, b] корень отделен.

Условия (1.2) –(1.4) – достаточные условия того, что корень на [a, b] отделен, то есть если эти условия выполняются, то корень отделен, но невыполнение, например, условий (1.3) или (1.4) не всегда означает, что корень не отделен.

Корень можно отделить аналитически и графически.

Пример. Аналитически отделить положительный корень уравнения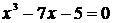

Решение. Составим таблицу

x
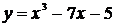	-5	-11	-11

1) f(2)f(3)<0

2) f(x) – непрерывная функция

3) 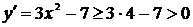, следовательно, f(x) – монотонно возрастает на отрезке [2, 3].

Вывод: на отрезке [2, 3] корень отделен.

Графический метод отделения корня

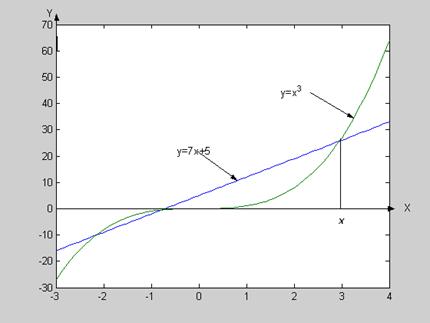
Уравнение 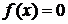представляют в виде j(x)=y(x), где j(x) и y(x) функции, более простые, чем f(x). Корень уравнения 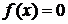- абсцисса точки пересечения графиков функций y=j(x) и y=y(x).

Пример: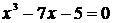

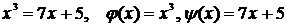
Метод касательных

Дополнительные предположения: f(x) дважды непрерывно дифференцируема на отрезке [a, b], на котором отделен корень; 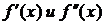сохраняют постоянные знаки на отрезке [a, b].

За х₀ выбирается точка, в которой выполняется условие:

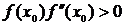(1.5)

Это либо точка a, либо точка b. Далее вычисляются точки

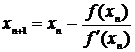(1.6)

до тех пор, пока не выполнится условие

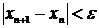(1.7) Тогда 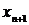- приближенное значение корня с погрешностью e.

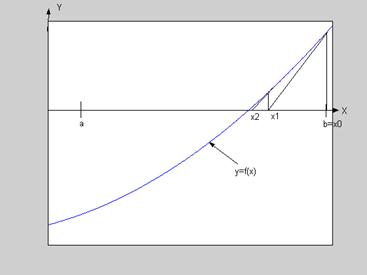
Для решения уравнений, в том числе трансцендентных, в Scilab применяют функцию fsolve(x0,f)

где x0 - начальное приближение, f - функция, описывающая левую часть уравнения f(x)=0.

Систему нелинейных уравнений также можно решить, используя функцию fsolve.

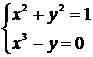
clc

function [y]=ff(x)

y(1)=x(1)^2+x(2)^2-1;

y(2)=x(1)^3-x(2);

endfunction

t=fsolve([-.5,-.5],ff)

t = - 0.8260314 - 0.5636242

Тема 2. Аппроксимация

Аппроксимация – замена одной функции f(x) другой, похожей функцией Q(x). Например, функцию, полученную экспериментально в виде таблицы или графика, надо записать в аналитическом виде, либо функцию, достаточно сложную нужно заменить похожей, но более простой.

Простейший способ аппроксимации – замена функции f(x) алгебраическим полиномом

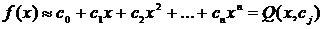(2.1)

Аппроксимацию называют точечной, если f(x) задана на конечном множестве точек (узлов)

Если f(x) задана на непрерывном множестве значений аргументов, то аппроксимацию называют интегральной.

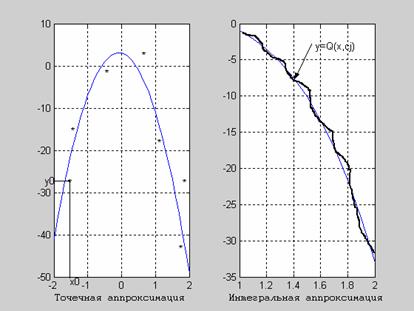
Необходимо так подобрать коэффициенты в формуле (2.1), чтобы Q(x,c_j) как можно меньше отличалась от f(x).

Метод наименьших квадратов

Чаще всего при точечной аппроксимации используют меру

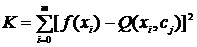(2.2)

а коэффициенты с_j ищут из условия

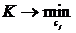(2.3)

Это точечная квадратичная аппроксимация.

При интегральной аппроксимации

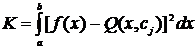
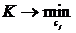
Описанный подход к задаче аппроксимации называется методом наименьших квадратов. Условия (2.2) и (2.3) геометрически означают: из всех кривых заданного вида выбирают ту, у которой сумма площадей квадратов отклонений – наименьшая.

В математике кривую y=Q(x,c_j) называют регрессией Y на X . Это означает, что у функции y=Q(x,c_j) число искомых коэффициентов меньше количества узлов, в крайнем случае возможно равенство

n+1£m+1 (2.4)

Если аргументом считать y, а x – функцией, то говорят о регрессии X на Y. Отклонения в этом случае откладывают по оси X.

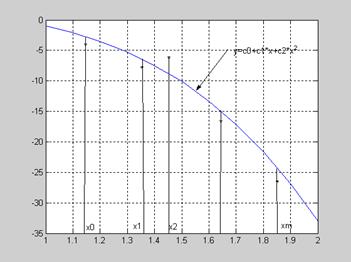
Регрессия Y на X

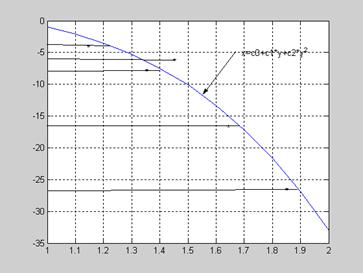
Регрессия X на Y

2.2 Нахождение коэффициентов c_j при точечной аппроксимации методом наименьших квадратов

Минимальное значение K в формуле (2.2) достигается при тех с_j , при которых

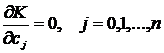(2.5)

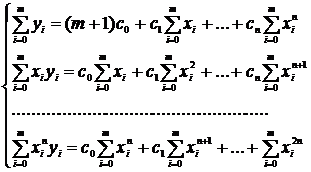(2.6)

Здесь x_i и y_i – заданные числа.

Пример: построить аппроксимирующую параболу для функции

x
y	-1,2	-0,1	1,3	1,8

Составим таблицу

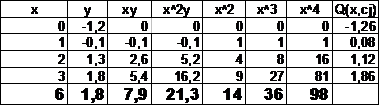
Запишем систему нормальных уравнений для нашей кривой.

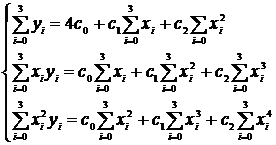или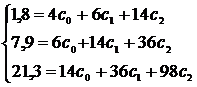

Решая систему, получаем:

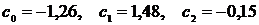или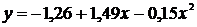

Вычисляя K по формуле (2.9), получаем: K=0,0720. У любой параболы второй степени значение K, вычисленное по формуле (2.9), будет больше, чем 0,0720.

Неполиномиальная регрессия

Часто на практике возникает следующая задача. Имеется объект исследования (ОИ), который характеризуется набором переменных: входных ( 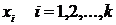) и выходной y.

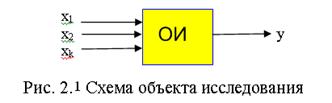
Требуется найти зависимость выходной переменной от входных

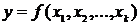( 2.7 )

При этом считается, что механизмы процессов, протекающих внутри объекта исследования, неизвестны, а имеются только соответствующие значения входных и выходных параметров. Такая задача носит название задачи «черного ящика».

Рассмотрим простейший случай, когда на вход действует только одна переменная x и требуется найти

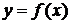( 2.8 )

Решение задачи моделирования в этом случае состоит из 4 этапов:

1) проведение эксперимента

2) выбор вида экспериментальной зависимости

3) нахождение параметров выбранной зависимости

4) исследование модели и выводы.

На первом этапе задаем значения входной переменной x из возможного диапазона и замеряем соответствующие значения выходной переменной y.

x	x0	x1	…	xm
y	y0	y1	…	ym

По экспериментальным данным строим график

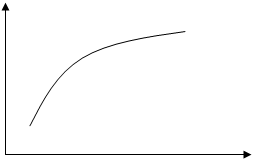Рис. 2.2 Экспериментальная кривая

На втором этапе необходимо выбрать формулу, которая могла бы описать экспериментальные данные. Во втором столбце таблицы 2.1 приведены основные типовые формулы, наиболее часто встречающиеся в задачах химии и химической технологии.

Таблица 2.1

№	Формула	Средние точки

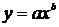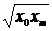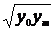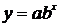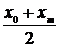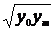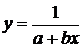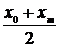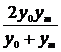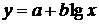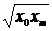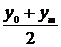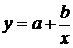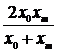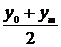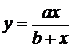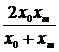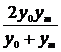Здесь х₀, y₀ – первая, а х_m , y_m – последняя точки исходной таблицы.

Для каждой функции рассчитывается средняя точка. Все эти точки наносятся на график с экспериментальной кривой.

Выбирается та кривая, средняя точка которой находится ближе всего к экспериментальной кривой. Покажем, как решается эта часть задачи на конкретном примере.

Пусть x=[5 7 9 11 13];y=[2.5 4.9 8 12.1 16.9];

Тогда

xap =(5+13)/2=9

xgео =(5*13)^0.5= 8.06

xgar =2*5*13/(5+13)= 7.22

yap =(2.5+16.9)/2= 9.7

ygeo = (2.5*16.9)^0.5= 6.5

ygar = 2*2.5*16.9/(2.5+16.9)= 4.36

Средняя точка для первой кривой –(8.06, 6.5)

Средняя точка для второй кривой –(9, 6.5)

Средняя точка для третьей кривой –(9, 4.36)

Средняя точка для четвертой кривой –(8.06, 9.7)

Средняя точка для пятой кривой –(7.22, 9.7)

Средняя точка для шестой кривой –(7.22, 4.36)

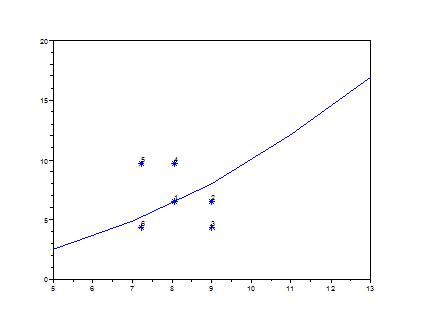
Нанесем на график исходные данные (х и у) и соединим соседние точки отрезками прямых. На этот же график нанесем средние точки для каждой кривой, снабдив их соответствующими номерами.

Эту часть задачи можно решить, построив график на Scilab.

clc

xbasc()

x=[5 7 9 11 13];y=[2.5 4.9 8 12.1 16.9];

n=length(x);

xap=(x(1)+x(n))/2

xgar=2*x(1)*x(n)/(x(1)+x(n))

xgeo=(x(1)*x(n))^.5

yap=(y(1)+y(n))/2

ygar=2*y(1)*y(n)/(y(1)+y(n))

ygeo=(y(1)*y(n))^.5

t=[xgeo xap xap xgeo xgar xgar]

z=[ygeo ygeo ygar yap yap ygar]

plot(x,y)

plot(t,z,'*')

for i=1:6

xnumb(t(i),z(i),i)

end

Из графика видно, что ближе всего к экспериментальной кривой лежит точка с номером 1, поэтому таблично заданную функцию будем заменять первой кривой .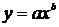

Приведем полученную кривую к линейному виду.

Кривую 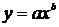(как и любую другую из таблицы 2.1) приводят к линейному виду (то есть к виду 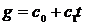) заменой переменных. 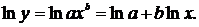В этом случае g=lny, c₀=lna, c₁=b, t=lnx.

Коэффициенты (параметры) с₀ и с₁ находят методом наименьших квадратов, то есть добиваются того, чтобы 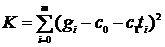было минимальным. Эта задача сводится к решению системы нормальных уравнений:

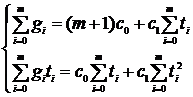или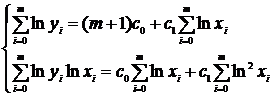

В нашем примере получается система:

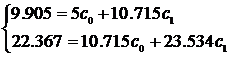
Решая ее, получаем с₀=- 2.294 с₁= 1.995

Зная с₀ и с₁ , находят a и b. В нашем примере

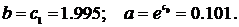
Таким образом, мы заменили таблично заданную функцию кривой .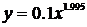

Подставляя в полученную формулу с конкретными значениями a и b значения x₀, x₁, … , x_m и сравнивая их с исходными данными, делают выводы об адекватности математической модели.

В нашем случае модель получилась адекватной.

x	y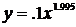
	2.5	2.480
	4.9	4.853
		8.011
	12.1	11.956
	16.9	16.685

Решим эту часть задачи на scilab.

Решение.

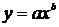. Покажем, как найти неизвестные коэффициенты a и b на Scilab.

clc

xbasc()

function [zr]=F(c,z)

zr=z(2)-(c(1)*z(1)^c(2))

endfunction

x=[5 7 9 11 13];

y=[2.5 4.9 8 12.1 16.9];

z=[x;y];

c=[1;1];

[d,S]=datafit(F,z,c)

t=5:.01:13;

Yt=(d(1)*t^d(2));

plot2d(x,y,-3);

plot2d(t,Yt);

S = 0.0067979

d = 0.0973802 2.0102774

В ответе d(1)= 0.0973802 это a, d(2)= 2.0102774 это b.

Таким образом, уравнение кривой, полученной на scilab,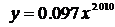

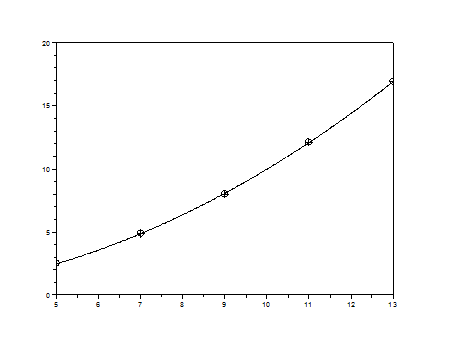
x	y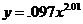
	2.5	2.464
	4.9	4.846
		8.032
	12.1	12.022
	16.9	16.819

Тема 3. Интерполяция

Интерполяция – частный случай аппроксимации, когда аппроксимирующая кривая проходит через все точки таблицы, то есть

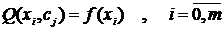(3.1)

Задача интерполяции ставится так:

Функция y=f(x) задана в виде таблицы

x	x0	x1	…	xm
y	y0	y1	…	ym

Требуется вычислить значение функции в точке x, не совпадающей ни с одним из узлов таблицы. Если эта точка лежит между узлами, то такая задача называется интерполяцией. Если точка x лежит за пределами таблицы, то говорят о задаче экстраполяции.

Очевидно, что коэффициенты с_j можно найти методом наименьших квадратов, положив n=m.

Рассмотрим другие способы решения этой задачи.

Интерполяция по Лагранжу

Построим полином

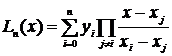(3.2)

Выражение (3.2) – алгебраический полином степени n. Покажем, что он проходит через все точки таблицы при n=2 и n=3.

; ; ;

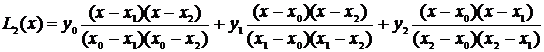
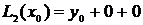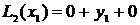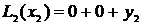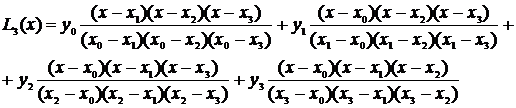
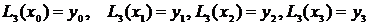
Выражение (3.2) – интерполяционный полином Лагранжа, проходящий через все точки таблицы. Теперь, чтобы найти значение функции в некоторой точке x^* , которой нет в таблице, достаточно подставить эту точку вместо x в формулу (3.2) и считать, что

y^*=L_n(x^*) (3.3)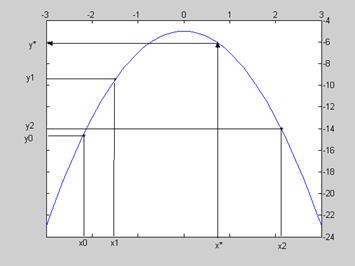

Обратная интерполяция

Постановка задачи:

Функция y задана в виде таблицы

x	x0	x1	…	xn
y	y0	y1	…	yn

Требуется найти значение аргумента x^*, при котором функция принимает некоторое значение y^*.

Задачу можно решить по крайней мере двумя различными способами.

1. а) Строим интерполяционный полином (как правило, ИПЛ)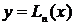

в) Решаем уравнение 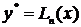любым подходящим численным методом (например, методом деления отрезка пополам).

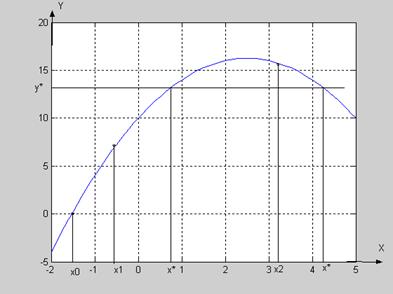
Из рисунка видно, что задача может иметь не единственное решение.

2. а) Строим интерполяционный полином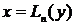

в) Подставляем в этот полином значение y^* и получаем x^*:

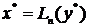( 3.8 )

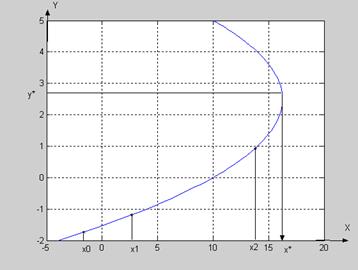
Как правило, решения задачи, полученные первым и вторым способом, будут различными.

Численное дифференцирование

Численное дифференцирование – это вычисление производных от функций, заданных в виде таблицы. Задача решается в два этапа. На первом этапе строится интерполяционный полином. На втором этапе находятся производные (первая, вторая и т.д.) от этого полинома.

Если шаг постоянный, то на первом этапе строят ИПН.

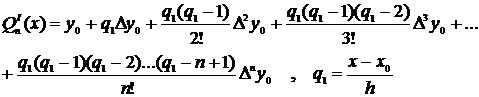
Найдем первую производную от этого полинома.

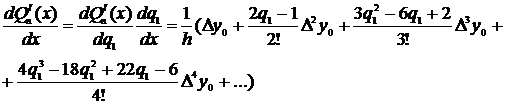( 3.9 )

Аналогично,

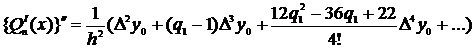( 3.10 )

Если производную нужно вычислить в каком-либо узле таблицы (например, в точке х=х₀), то формулы (3.9) и (3.10) упрощаются, так как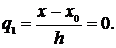

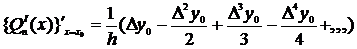( 3.11 )

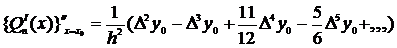( 3.12 )

Задача численного дифференцирования относится к числу некорректных задач. Это означает, что сколь угодно малые погрешности в исходных данных могут привести к большим погрешностям результата решения, поэтому к численному дифференцированию не следует прибегать без особой необходимости. По тем же причинам обычно не вычисляют производные старших порядков.

Нахождение значения производной в заданной точке на Scilab:

Найти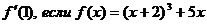

clc

function y=f(x)

y=(x+2).^3+5*x;

endfunction

numdiff(f,1)

ans =

32.

Метод Эйлера

Перепишем уравнение (4.7) в виде

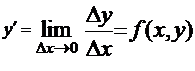
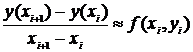Обозначим 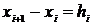. Тогда

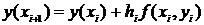(4.8)

Формула (4.8) – формула метода Эйлера решения ОДУ первого порядка.

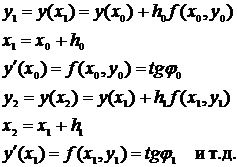
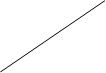
Y *

*

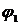
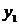
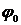
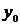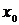
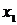
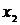X

Результатом численного решения дифференциального уравнения является таблица

X				…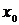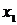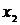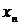
Y				…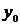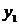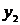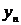

где 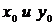заданы, 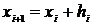(шаг h_i задается и может быть как переменным, так и постоянным, а y_i (i=1, 2, … , n) вычисляются по соответствующим формулам (например, по формуле (4.8)).

Пример:

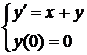h=0.2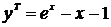

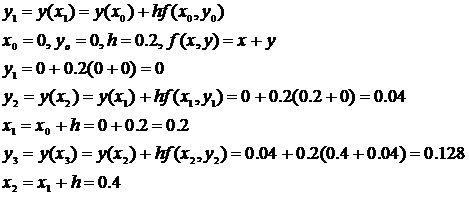
x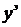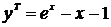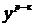
0.2		0.021403	0.0214
0.4	0.04	0.091825
0.6	0.128	0.222119

Погрешность метода Эйлера – o(h).

Тема 1. Численные методы решения уравнений

Уравнение называется алгебраическим, если его можно представить в виде:

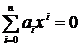(1.1)

Формула (1.1) – каноническая форма записи алгебраического уравнения. Если уравнение 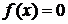не удается привести к виду (1.1) заменой переменных, то уравнение называется трансцендентным.

Решить уравнение означает найти такие значения x, при которых уравнение превращается в тождество.

Известно, что уравнение (1.1) имеет ровно n корней – вещественных или комплексных. Если n=1, 2, 3 [и иногда 4 (биквадратное уравнение], то существуют точные методы решения уравнения (1.1). Если же n>4 или уравнение – трансцендентное, то таких методов не существует, и решение уравнения ищут приближенными методами. Всюду при дальнейшем изложении будем предполагать, что f(x) – непрерывная функция. Методы, которые мы рассмотрим, пригодны для поиска некратных (то есть изолированных) корней.

Отделение корня

Решение уравнения состоит из двух этапов: 1 – отделение корня, 2 – его уточнение.

Отделить корень – значит указать такой отрезок [a, b] , на котором содержится ровно один корень уравнения .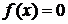

Не существует алгоритмов отделения корня, пригодных для любых функций f(x). Если удастся подобрать такие a и b, что

1) f(a) f(b)<0 (1.2)

2) f( x) – непрерывная на [a, b] функция (1.3)

3) f( x) – монотонная на [a, b] функция (1.4)

то можно утверждать, что на отрезке [a, b] корень отделен.

Условия (1.2) –(1.4) – достаточные условия того, что корень на [a, b] отделен, то есть если эти условия выполняются, то корень отделен, но невыполнение, например, условий (1.3) или (1.4) не всегда означает, что корень не отделен.

Корень можно отделить аналитически и графически.

Пример. Аналитически отделить положительный корень уравнения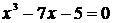

Решение. Составим таблицу

x
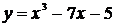	-5	-11	-11

1) f(2)f(3)<0

2) f(x) – непрерывная функция

3) 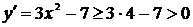, следовательно, f(x) – монотонно возрастает на отрезке [2, 3].

Вывод: на отрезке [2, 3] корень отделен.