Какой общий вид имеет полином, используемый для аппроксимации зависимостей по методу наименьших квадратов?

Вариант ответов:

а) .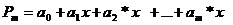

б) .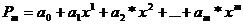

в) .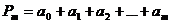

г) .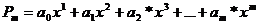

3.6 Какое выражение можно назвать конечными разностями 1-го порядка:

Вариант ответов:

а) у₃-у₄

б)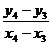

в) y_i-y_i-1

г) x_i-x_i-1

3.7 График функции обязательно должен проходить через заданные точки х и у построенный по:

Вариант ответов:

а) многочлену Лагранжа

б) методу наименьших квадратов

в) многочлену Ньютона

г) все ответы верны

3.8 Какие средства имеются в MathCad для сплановой интерполяции:

Вариант ответов:

а) interp(vs,vx,vy,x)

б) linterp(vx,vy,x)

в) lsolve(A,B)

г) rkfixed(y₀,a,b,n,D)

3.9 Среднеквадратичное отклонение вычисляется по формуле:

Вариант ответов:

а)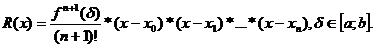

б)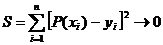

в)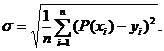

г)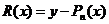

3.10 Погрешность интерполяции определяется разностью :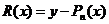

Вариант ответов:

а) В многочлене Лагранжа

б) В методе наименьших квадратов

в) В многочлене Ньютона

г) Все ответы верны

3.11 Функционал для определения коэффициентов а_i методом наименьших квадратов находится по формуле:

Вариант ответов:

а)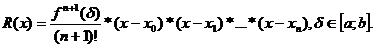

б)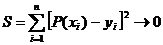

в)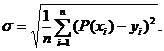

г)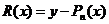

3.12 График построенной функции 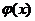должен проходить через все экспериментально полученные точки (х_i, y_i) при :

Вариант ответов:

а) Интерполировании;

б) Аппроксимации

в) Это желаемое требование, но не обязательное;

г) Обязательно при интерполировании и аппроксимации;

3.13 Погрешность вычисляется по формуле:

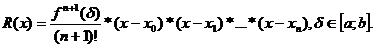для :

Вариант ответов:

а) многочлена Лагранжа

б) метода наименьших квадратов

в) многочлена Ньютона

г) Все ответы верны

3.14 В MathCad можно найти значения функции у в промежуточных точках с помощью полинома некоторой степени. Для этого используются следующие функции:

Вариант ответов:

а) regress(vx,vy,k)

б) interp(vs,vx,vy,x)

в) root(f(x),x)

г) lsolve(A,B)

3.15 Для определения коэффициентов а_i методом наименьших квадратов при решении системы уравнений использовались следующие обозначения:

Вариант ответов:

а)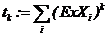

б)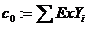

в)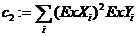

г) Все ответы верны

4. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ И ДИФФЕРЕНЦИРОВАНИЕ

4.1 Формула Ньютона-Лейбница для вычисления определенного интеграла имеет вид:

Вариант ответов:

а) .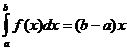

б) .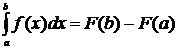

в) .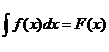

г) .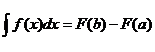

4.2 Формула 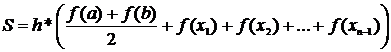используется для вычисления определенного интеграла методом:

Вариант ответов:

а) Трапеций.

б) Симпсона.

в) По формуле Ньютона-Лейбница.

г) Нет правильного ответа

4.3 Формула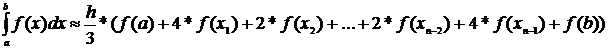

используется для вычисления определенного интеграла методом:

Вариант ответов:

а) Трапеций.

б) Симпсона.

в) По формуле Ньютона-Лейбница.

г) Прямоугольников

4.4 С геометрический точки зрения определенный интеграл функции f(x) на отрезке [a; b] численно равен площади, ограничиваемой:

Вариант ответов:

а) Графиком функции y = f(x) и прямыми x = a, x = b.

б) Графиком функции y = f(x), осью абсцисс и осью ординат.

в) Графиком функции y = f(x), осью ординат и прямыми x = a, x = b.

г) Графиком функции y = f(x), осью абсцисс и прямыми x = a, x = b.

4.5 Оценка погрешности усечения метода трапеций вычисляется по формуле 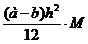, где М=:

Вариант ответов:

а) min ( f “(x)), a 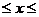b

б) max (f “(x)), a 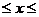b

в) (f ’’’’(x)), a b.

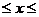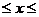г) (f “(x)), a b

4.6 Производная функции в некоторой точке численно равна:

Вариант ответов:

а) Синусу угла, образуемого касательной, проведенной через точку, в которой считается производная и осью абсцисс.

б) Тангенсу угла, образуемого касательной, проведенной через точку, в которой считается производная и осью ординат.

в) Котангенсу угла, образуемого касательной, проведенной через точку, в которой считается производная и осью абсцисс.

г) Тангенсу угла, образуемого касательной, проведенной через точку, в которой считается производная и осью абсцисс.