Коэффициенты детерминации и корреляционные отношения

Коэффициенты детерминации определяются по формулам:

;

,

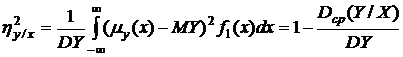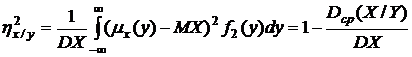где 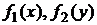– одномерные плотности вероятности;

; ;

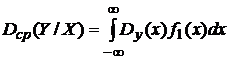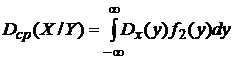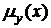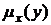, – условные математические ожидания;

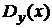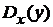, – условные дисперсии.

Часто 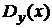=σ²= const, тогда 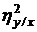=1– .

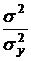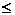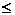Можно показать, что 0 ρ² η² 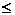1, где ρ – коэффициент корреляции. Равенство η²=ρ²имеет место лишь при линейных функциях , .

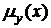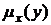Корреляционным отношением называют корень квадратный из коэффициента детерминации, взятый со знаком плюс, т.е. – величину η= .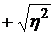

Двумерное нормальное распределение.

Плотность вероятности:

,

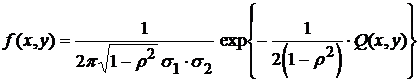где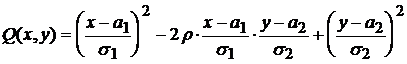

В общем случае график f(x,y) имеет вид сплюснутого с боков колокола, в сечениях которого – эллипсы: 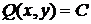. При 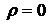главные оси эллипсов параллельны осям координат. Есл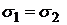и и 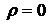, то сечениями являются окружности.

Пользуясь формулами в п.2.4.5 и п.2.4.6, можно определить, что 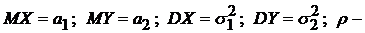коэффициент корреляции.

Если 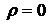, то, подставляя этот ноль в формулу для двумерной плотности распределения, получим: 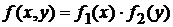, т. е. для нормального распределения из некоррелированности случайных величин следует их независимость.

Условную плотность распределения 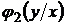нетрудно получить, используя формулы для одномерного и двумерного нормального распределений:

,

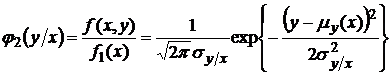где условное математическое ожидание и условная дисперсия:

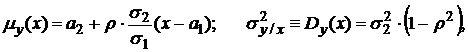
т. е. уравнение регрессии 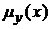является линейной функцией, а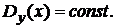

Аналогично можно определить условную плотность распределения .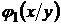

Второе уравнение регрессии: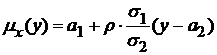

Оба уравнения регрессии можно записать иначе:

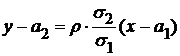
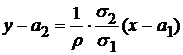
Уравнения этих прямых проходят через точку 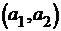и совпадают только при детерминированной зависимости между X и Y , т.е. при .

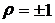2.4.8. Показатели статистической зависимости СВ.

Общий случай

Пусть имеется система, состоящая из k случайных величин: 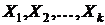. Пусть известна функция распределения 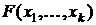или плотность распределения 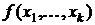. На практике большое распространение получило нормальное распределение, плотность которого имеет вид:

f (x₁,x₂,…,x_k) = ,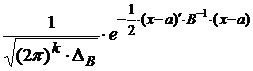

где (х-а) и (х-а)′ – вектор-столбец, соответственно, вектор-строка переменных, состоящие из элементов х_i-a (i=1,2,…,k);

B^-1– матрица, обратная ковариационной матрице B=(К_ij)≡(cov(X_i,X_j));

Δ_B– определитель матрицы B.

В частности, при k=2 имеем:

B= 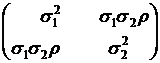; B^-1= 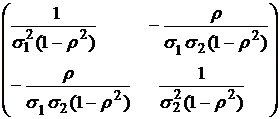; Δ_B= ;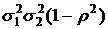

(х-а)′B^-1(х-а) =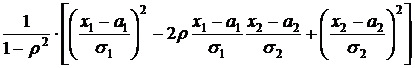

Подставляя полученные выражения в формулу для f (x₁,x₂,…,x_k) при k=2, получим выражение для двумерной плотности вероятности нормально распределенной случайной величины, приведенное ранее.

При k≥3, по аналогии с тем, как одномерные распределения выражаются через двумерные, можно получить двумерные распределения для каждой пары X_i, X_j (i ≠ j): для НСВ – плотности 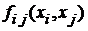, для ДСВ – матрицы ( 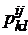) вероятностей произведения событий: 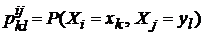. Определяя для каждой пары ковариации и коэффициенты корреляции, получим ковариационную матрицу (К_ij), по главной диагонали которой будут стоять дисперсии, и корреляционную матрицу 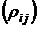, по главной диагонали которой будут стоять единицы, причем К_ij= К_ji и = .

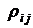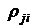Функция распределения зависит от условий проведения испытаний или наблюдений. Значит, от этих условий зависят и 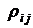. Пусть, например, испытания будут проведены теперь при некоторых фиксированных значениях всех случайных величин, кроме X₁ и X₂. Если 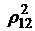при этом уменьшится, то можно сделать вывод, что взаимозависимость между X₁ и X₂ во многом (или даже в значительной степени) была вызвана действием других (ныне фиксированных) факторов. И наоборот, если 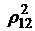увеличится, то это будет означать, что другие факторы маскировали истинную взаимозависимость между X₁ и X₂. Поэтому, наряду с 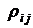(их называют коэффициентами парной корреляции) используют и другие показатели статистической зависимости: множественные коэффициенты корреляции и частные коэффициенты корреляции.