С постоянными коэффициентами и специальной правой частью

Уравнение вида 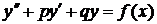, где p, q – заданные числа называется линейным неоднородным дифференциальным уравнением (ЛНДУ) второго порядка с постоянными коэффициентами.

Линейное ДУ второго порядка без правой части 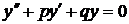, соответствующее ЛНДУ, называется линейным однородным дифференциальным уравнением(ЛОДУ).

Теорема (о структуре общего решения ЛНДУ). Общим решением ЛНДУ является сумма его общего решения у_оо соответствующего ЛОДУ и произвольного частного решения у_чн, то есть у = у_чн + у_оо.

Рассмотрим нахождение общего решения у_оо и частного решения у_чн.

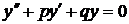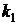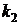Пусть дано ЛОДУ второго порядка . Если и – корни характеристического уравнения 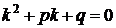(для этого необходимо 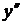заменить 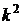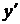на , – на 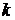, 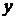– на1), то общее решение записывается в одном из следующих трех видов (табл. 1):

Общее решение линейного однородного дифференциального

уравнения второго порядка

Таблица 1.

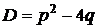	Корн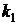и и	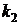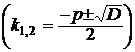Общее решение ЛОДУ
1)	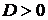действительные и различные ( )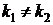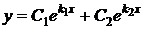
2)	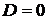действительные и равные ( )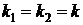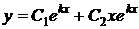
3)	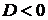комплексные 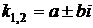(а и b – действительные числа)

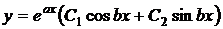Пример 14. Найти общее решение уравнения .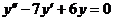

Решение. Составим характеристическое уравнение 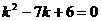и найдем его корни: 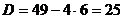; ; 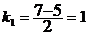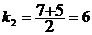. Т.к. 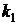и 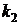– действительные и различные числа, то общее решение записывается в виде: .

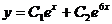Пример 15. Найти общее решение уравнения .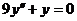

Решение. Характеристическое уравнение имеет вид: 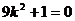, , 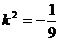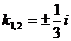– комплексно-сопряженные корни, 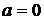, 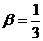. Общее решение имеет вид 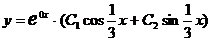, отсюда .

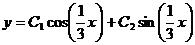Пример 16. Найти общее решение уравнения .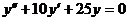

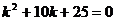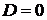
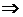
Решение. Характеристическое уравнение имеет вид: . Найдем его корни: 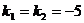. Тогда .

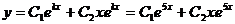Найдём теперь частное решение неоднородного уравнения

Рассмотрим следующие случаи:

1) Пусть правая часть неоднородного уравнения имеет вид 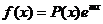, где P(x)-многочлен.

Тогда неоднородное уравнение имеет частное решение вида 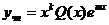, где Q(x)-многочлен той же степени, что и P(x), k-кратность корня характеристического уравнения, равного m(то есть сколько корней характеристического уравнения равно m).

Неизвестные коэффициенты многочлена Q(x) находим с помощью метода неопределённых коэффициентов.

Это правило верно и при m=0, когда правая часть есть многочлен. В частных случаях P(x) может быть и постоянной величиной (числом).

2) Пусть правая часть неоднородного уравнения имеет вид .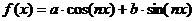

Если числа 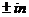являются корнями характеристического уравнения, то неоднородное уравнение имеет частное решение вида .

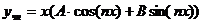Если числа 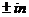не являются корнями характеристического уравнения, то неоднородное уравнение имеет частное решение вида .

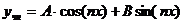Если a=0 или b=0, решение всё равно следует искать в общем виде.

3) Пусть правая часть неоднородного уравнения имеет вид 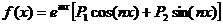, где P₁(x) и P₂(x) –многочлены.

Если числа m 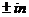являются корнями характеристического уравнения, то неоднородное уравнение имеет частное решение вида .

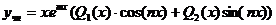Если числа 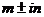не являются корнями характеристического уравнения, то неоднородное уравнение имеет частное решение вида .

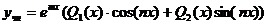Q₁(x) и Q₂(x)-многочлены степени, равной высшей из степеней многочленов P₁(x) и P₂(x)

Замечание. Частное решение ЛНДУ имеет тот же вид, что и специальная правая часть, но если число 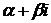является корнем характеристического уравнения кратности r, то в частном решении присутствует множитель .

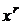Немногим более сложные виды специальной правой части рекомендуем разобрать самостоятельно.

Пример 17. Решить уравнение , ,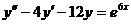

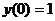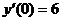
Решение.Данное уравнение является линейным неоднородным дифференциальным уравнением второго порядка со специальной правой частью 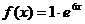( 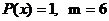) Соответствующее однородное уравнение имеет вид .

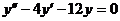Составим характеристическое уравнение 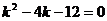и найдем его корни: , .

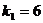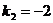Тогда общее решение ЛОДУ имеет вид .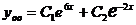

Найдем частное решение ЛНДУ. Т.к. 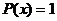, , 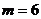и число 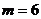является простым (однократным) корнем характеристического уравнения (совпадает с 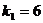), то частное решение будем искать в виде 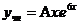. Для отыскания неопределенного коэффициента А подставим 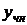в данное линейное неоднородное дифференциальное уравнение, предварительно вычислив 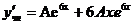, 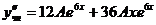. Получаем равенство

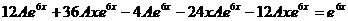, откуда находим 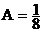. Таким образом .

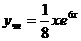Так как. общее решение линейного неоднородного дифференциального уравнения находится в виде 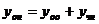, то окончательно получаем .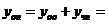

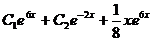Теперь подставим начальные условия в полученное решение, получим

, ,

,

, .

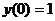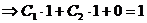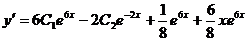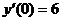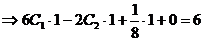Решив систему, получаем , .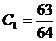

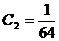Частное решение, удовлетворяющее заданным начальным условиям,

.
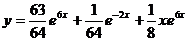