Наибольшее и наименьшее значение функции двух переменных
Для того чтобы найти наибольшее и наименьшее значение функции в замкнутой области надо:
1. найти критические точки, расположенные в данной области, вычислить значения функции в этих точках;
2. найти наибольшее и наименьшее значения функции на линиях, образующих границу области;
3. из всех найденных значений выбрать наибольшее и наименьшее.
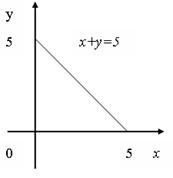
Пример 22.Найти наибольшее и наименьшее значения функции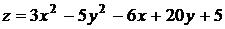 
в замкнутом треугольнике, ограниченном осями координат и прямой 
.
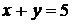Рис.22
Решение.
1. Найдём критические точки из системы 
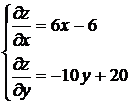
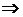
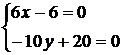
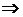
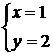
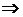(1; 2) – критическая точка, которая принадлежит заданной области. Значение функции в критической точке 
.
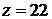1. Проводим исследование на границе.
На прямой Оу получаем: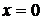 
, 
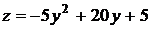. Исследуем эту функцию одной переменной на наибольшее и наименьшее значения на интервале 
.
.
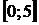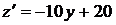
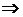
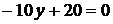
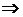
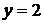
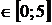
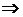
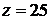На концах отрезка 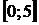функция принимает значения 
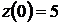и 
.
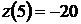На прямой Ох получаем: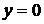 
, 
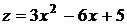. Исследуем эту функцию одной переменной на наибольшее и наименьшее значения на интервале .
.
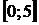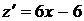
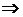
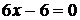
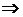
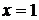
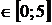
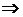
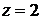На концах отрезка 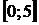функция принимает значения 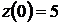и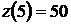 
.
На прямой 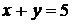получаем: 
, 
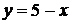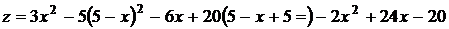. Исследуем эту функцию одной переменной на наибольшее и наименьшее значения на интервале .
.
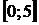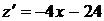
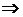
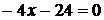
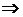
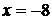
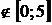На концах отрезка 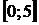функция принимает значения 
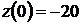и .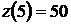
3. Из всех получившихся значений выбираем наибольшее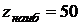 
и наименьшее 
.
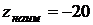Пример 23. Из всех прямоугольных треугольников с заданной площадью S найти такой, гипотенуза которого имеет наименьшее значение.
Решение. Пусть x и y– катеты треугольника, а z–гипотенуза. Так как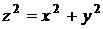 
, то задача сводится к нахождению наименьшего значения функции 
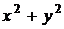при условии, что x и y связаны уравнением 
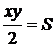, т.е. 
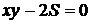. Рассмотрим функцию 
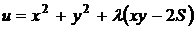и найдём частные производные 
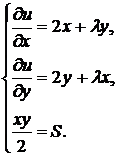Получаем решение 
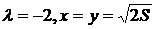. Таким образом, гипотенуза имеет наименьшее значение, если катеты треугольника равны между собой.
[1] Дирихле Петер Густав (1805-1859) – немецкий математик, член- корреспондент Петербургской АН 1837г.
[2] Вейерштрасс Карл (1815-1897)- немецкий математик.
[3] Кантор Георг (1845-1918)- немецкий математик.
[4] Лопиталь де Гийом Франсуа (1661-1704) – французский математик, член Парижской академии наук, ученик И.Бернулли. Автор первого учебника по дифференциальному исчислению «Анализ бесконечно малых» (1696г.); в этом учебнике и было сформулировано правило, называемое теперь правилом Лопиталя.
[5] Dх может быть и отрицательным.
[6] На этом рисунке знаком «+» отмечены те интервалы, на которых функция положительна, и знаком «-» те, где она отрицательна.
[7] Теорема Лагранжа.Если функция f(x) непрерывна на отрезке [a, b] и дифференцируема на интервале (а, b), то на этом интервале найдется, по крайней мере, одна точка e (a < e < b), такая, что .
[8] Геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического смысла дифференциала функции одной переменной.
[9] Другой способ решения смотрите пример в пункте 3.7.
[10] Можно было не искать, а сослаться на теорему Шварц.
[11] Лагранж Жозеф Луи (1736-1813) – французский математик и механик, член Берлинской академии наук (1759), Парижской академии наук (1772), почётный член Петербургской академии наук (1776), родился и получил высшее образование в Турине (Италия).