Сравнение бесконечно малых функций. Эквивалентные бесконечно малые
Замечание: функции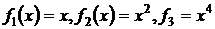 
при 
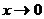бесконечно малые величины, но к нулю они стремятся по-разному.
Чтобы сравнить бесконечно малые функции рассматривают предел их отношения. Пусть функци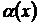и 
и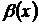 
являются бесконечно малыми при 
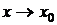. Рассмотрим предел отношения этих функций при 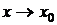и введем следующие определения.
Функции 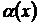и 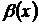называются бесконечно малыми одного и того же порядка малости при 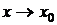; если 
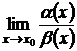есть конечное число, отличное от нуля.
Функция 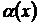называется бесконечно малой более высокого порядка малости, чем функция 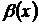при 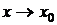, если 
.
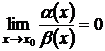Функция 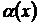называется бесконечно малой более низкого порядка малости, чем функция 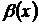при 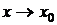, если 
.
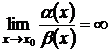Функции 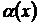и 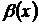называются несравнимыми бесконечно малыми при 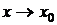, если 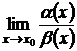не существует.
Пример 13.
Функция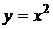 
является бесконечно малой при 
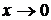более высокого порядка малости, чем функция 
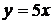, так как 
.
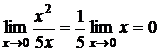При приближении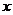 
к нулю функция 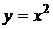стремится к нулю быстрее, чем функция .
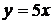Пример 14.
Функция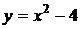 
и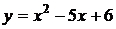 
являются бесконечно малыми одного порядка малости при 
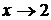, так как 
.
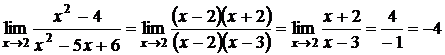Введем теперь понятие эквивалентных бесконечно малых функций.
Две функци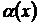и и 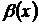бесконечно малые при ( 
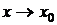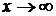) называются эквивалентными (или равносильными), если предел их отношения при 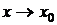( 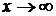) равен единице.
Например, функции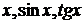 
являются эквивалентными бесконечно малыми функциями при 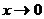, так как 
, 
.
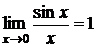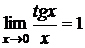Есл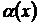и и 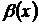– эквивалентные бесконечно малые функции, то это записывают так: 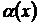~ 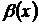или ~ .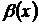
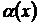Таблица эквивалентных бесконечно малых
Таблица 3
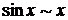 при |  при |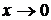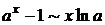
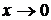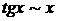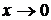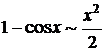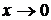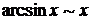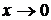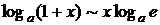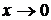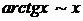 при 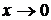| 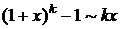 при |
 при 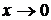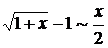|  при |
 при 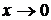| 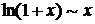 при  при |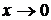
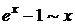 при | |
 при |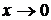
Пример 15. Найти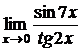 
.
Решение. Так как при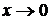 
~ 
, 
~ 
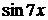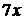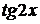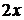то 
.
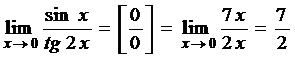Пример 16.Найти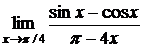 
.
Решение.
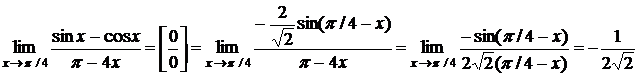
Пример 17.Найти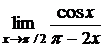 
.
Решение.
.
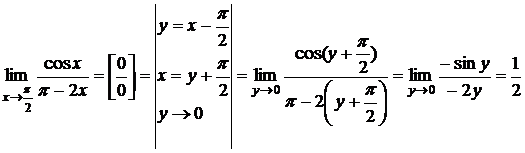Пример 18.Найти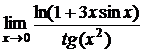 
.
Решение. Так как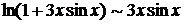 
, а 
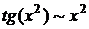, то
.
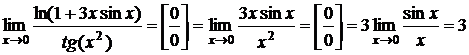Пример 19.Найти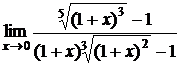 
.
Решение. Так как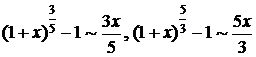 
, то
.
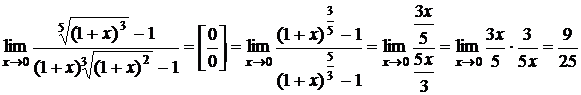Непрерывность функции в точке
Функция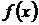 
, определенная в окрестности некоторой точки х0, называется непрерывной в точкех0, если предел функции и ее значение в этой точке равны, т.е. 
.
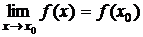Равенство означает выполнение трех условий:
1. функция 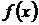определена в точке х0 и в ее окрестности;
2. функция 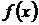имеем предел при ;
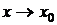3. предел функции в точке х0 равен значению функции в этой точке.
Если функция 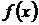определена в некоторой окрестности точки х0, но не является непрерывной в самой точке х0, то она называется разрывной функцией, а точка х0 – точкой разрыва.
Функция 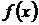называется непрерывной в точке х0, если для любого положительного числа e>0 существует такое число D>0, что для любых х, удовлетворяющих условию 
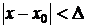верно неравенство 
.
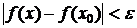Функция 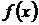называется непрерывной в точке х = х0, если приращение функции в точке х0 является бесконечно малой величиной.
= 
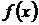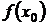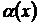+ , где 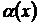– бесконечно малая при 
.
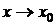Свойства непрерывных функций.
1) Сумма, разность и произведение непрерывных в точке х0 функций – есть функция, непрерывная в точке х0.
2) Частное двух непрерывных функций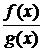 
– есть непрерывная функция при условии, что g(x) не равна нулю в точке х0.
3) Если u = f(x), v = g(x) – непрерывные функции в точке х = х0, то функция v = g(f(x)) – тоже непрерывная функция в этой точке.