Теоремы о пределах. Приемы вычисления пределов

Рассмотрим некоторые теоремы о правилах предельного перехода, которые облегчают нахождение пределов:

1) Если функцию 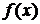можно представить в виде суммы постоянной величины 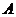и величины бесконечно малой 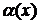, то постоянная величина 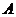— предел функции.

2) Если функция 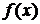имеет предел, равный 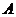, то ее можно представить как сумму числа 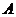и бесконечно малой функции.

3) Предел суммы конечного числа слагаемых равен сумме пределов этих слагаемых.

4) Предел произведения двух функций равен произведению их пределов.

5) Постоянный множитель можно выносить за знак предела.

6) Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю.

Пример 3. Найти .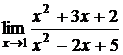

Решение. .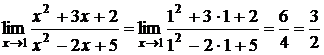

Непосредственное применение теории о пределах, однако, не всегда приводит к цели. Так, например, нельзя применять теорему о пределе дроби, если ее знаменатель стремится к нулю. Поэтому часто, прежде чем применять эти теоремы, необходимо преобразовать функцию, предел которой мы ищем. Как это делается покажем на конкретных примерах.

Пример 4. Найти .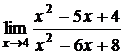

Решение. .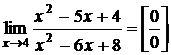

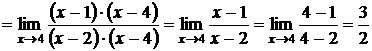Отыскание предела этой дроби сводится, как говорят, к раскрытию неопределенности 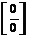, для этого преобразуем дробь, разложив числитель и знаменатель на множители: .

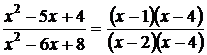Пример 5. Найти .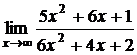

Решение.Здесь непосредственно применить теорему о пределе дроби нельзя, так как ни числитель, ни знаменатель дроби не имеют конечного предела при 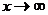, одновременно стремясь к бесконечности. В этом случае говорят, что дробь представляет неопределенность вида 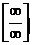. Для того, чтобы найти предел данной дроби, предварительно преобразуем ее, разделив числитель и знаменатель на 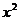(старшую степень); дробь от этого не изменит своей величины, а, следовательно, и своего предела. После этого преобразования предел уже найти легко:

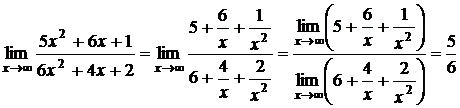
Пример 6. Найти .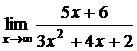

Решение. Для того чтобы и здесь можно было применить теорему о пределе частного, разделим числитель и знаменатель на 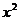(старшую степень).

.

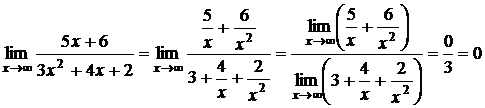Пример 7.Найти .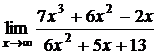

Решение. .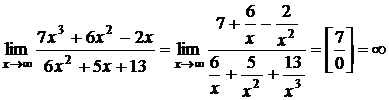

Замечание. При решении примеров 4-6 с неопределенностями вида 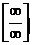мы делили числитель и знаменатель дроби на старшую из степеней 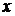, встречающихся в дробном выражении. Этот прием при условии, что 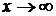, является общим и его следует запомнить.

Вычисляют пределы и с помощью некоторых специальных формул (замечательных пределов).

Первый замечательный предел

Первый замечательный предел: .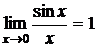

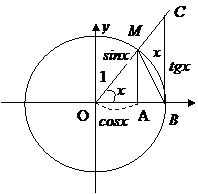Доказательство.Возьмем круг радиуса 1, обозначим радианную меру угла МОВ через х. Пусть 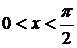. На рисунке 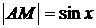, дуга МВ численно равна центральному углу х, 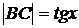. Очевидно, имеем .

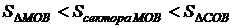Рис. 4

На основании соответствующих формул геометрии получаем 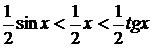. Разделим неравенство на 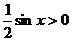, получим 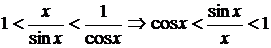. Так как 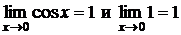- то по признаку (о пределе промежуточной функции) существования пределов .

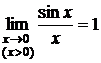А так как 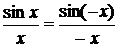, то

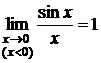
Пример 8. Найти .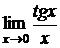

Решение. Числитель и знаменатель дроби при 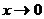одновременно стремятся к нулю. Теорема о пределе дроби здесь неприменима. Для отыскания предела преобразуем данную дробь:

.

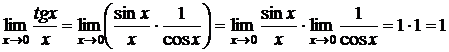Пример 9. Найти .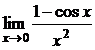

Решение. .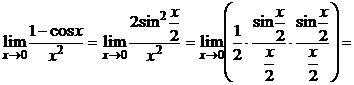

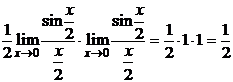Второй замечательный предел

Второй замечательный предел: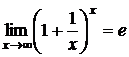

Докажем, что к числуестремится и функция x_n = 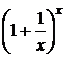при .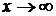

1. Пусть 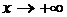. Каждое значение х заключено между двумя положительными целыми числами: 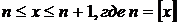- это целая часть х. Отсюда следует 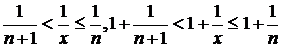, поэтому .

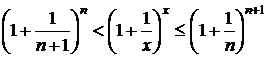Если 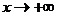, то .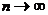

Поэтому имеем: ;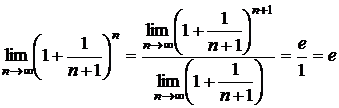

.

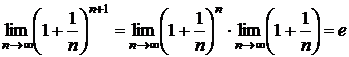По признаку существования пределов .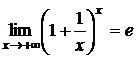

2. Пусть 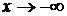. Сделаем подстановку –х=t, тогда

.

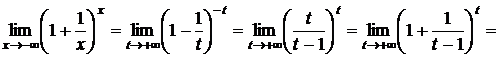
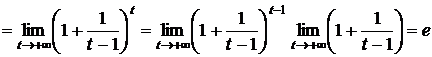
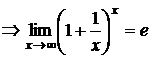Пример 10. Найти .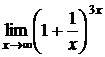

Решение.

1 способ.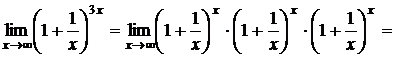

.

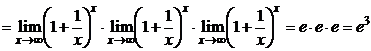2 способ. .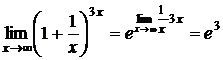

Замечание: для вычисления второго замечательного предела удобно пользоваться формулой .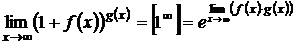

Пример 11. Найти .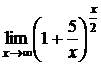

Решение. .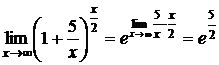

Пример 12. Найти .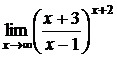

Решение.

=

= .
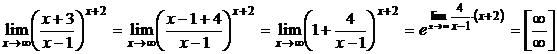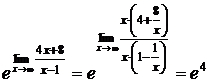