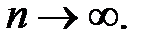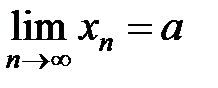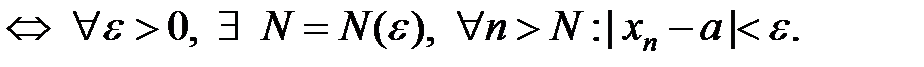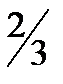1) 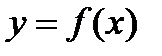 монотонная на D(f).
монотонная на D(f).
2) Решаем 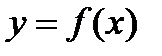 относительно x, т.е. находим
относительно x, т.е. находим 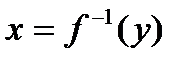 (по существу
(по существу 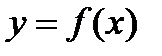 и
и 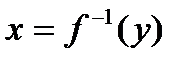 выражают одну и ту же зависимость, графики совпадают).
выражают одну и ту же зависимость, графики совпадают).
3) Переобозначаем переменные, т.е.  - обратная функция.
- обратная функция.
4) График

симметричен графику
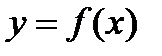
относительно биссектрисы первого координатного угла.
Пример1.7.  возраcтает на D=R;
возраcтает на D=R;

 обратная функция.
обратная функция.
IV. Основные элементарные функции. Самостоятельно. Графики функций:
1) постоянная y=c;
2) степенная 
а)  б)
б)  в)
в)  г)
г) 
3) показательная  . а)
. а)  б)
б) 
4) логарифмические: 
5) тригонометрические: 
6) обратные тригонометрические функции: 

V. Абсолютная величина действительного числа, ее свойства

 где
где  равносильно
равносильно  .
.
 где
где  равносильно
равносильно  или
или  .
.
Свойства:
1)  2)
2) 
3)  4)
4)  где
где 
Переменная величина. Упорядоченная переменная
def.Переменной называется величина, которая принимает различные численные значения.
Частный случай – постоянная величина, значение которой не меняется.
Переменные величины обозначают: x, y, z, а постоянные: a, b, c.
def. Совокупность всех числовых значений переменной величины называется областью изменения этой переменной.
def.Окрестностью данной точки x0 называется произвольный интервал (a,b), содержащий эту точку внутри себя.
Обычно рассматривается такая окрестность точки, для которой x0 является серединой.

окрестность точки x
0;
 центр окрестности;
центр окрестности;
 радиус окрестности.
радиус окрестности.
def. Переменная x является упорядоченной переменной величиной, если известна область изменения этой переменной величины и про каждое из двух любых ее значений можно сказать, какое значение предыдущее, а какое последующее.
Важный частный случай упорядоченной переменной является величина, значение которой образуют числовую последовательность.
def.Если каждому натуральному числу 1,2, 3, …, n, … поставить в соответствие некоторое действительное число, то получится числовая последовательность  члены которого занумерованы натуральными числами и расположены в порядке возрастания номеров. Последовательность обозначают
члены которого занумерованы натуральными числами и расположены в порядке возрастания номеров. Последовательность обозначают  или
или  , или
, или  .
.
Пример 2.1.
Предел упорядоченной переменной величины
I. Определение предела
Рассмотрим упорядоченную переменную, значения которой образуют числовую последовательность 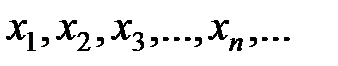
Пример3.1. 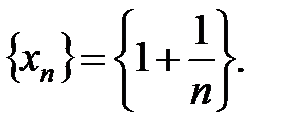
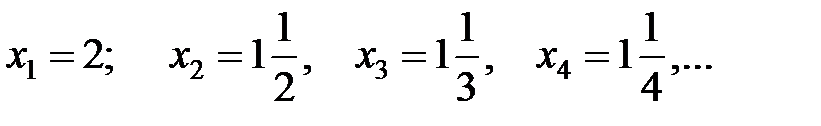
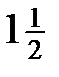 2\4 2\4 |
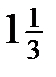 2\4 2\4 |
Значения переменной приближаются к 1, сгущаются около 1 (но никогда 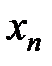 не примет значение, равное 1).
не примет значение, равное 1).
def. Число а называется пределом переменной 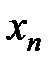 (пределом числовой последовательности), если для любого сколь угодно малого положительного числа
(пределом числовой последовательности), если для любого сколь угодно малого положительного числа 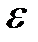 найдется такой номер N, зависящий от
найдется такой номер N, зависящий от 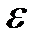 , что для всех значений
, что для всех значений 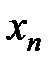 , у которых n>N, будет выполняться неравенство
, у которых n>N, будет выполняться неравенство 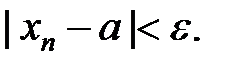
Обозначают: 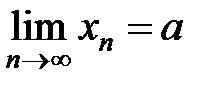 или
или 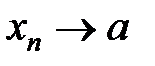 при
при 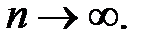
Определение предела на языке символов:
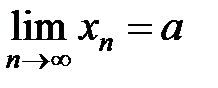
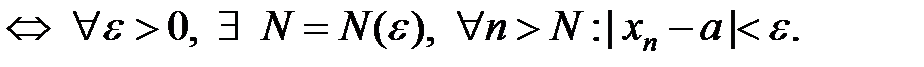
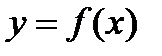 монотонная на D(f).
монотонная на D(f).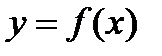 относительно x, т.е. находим
относительно x, т.е. находим 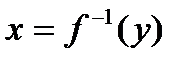 (по существу
(по существу 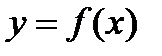 и
и 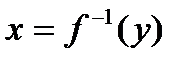 выражают одну и ту же зависимость, графики совпадают).
выражают одну и ту же зависимость, графики совпадают). - обратная функция.
- обратная функция.

 симметричен графику
симметричен графику 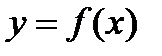 относительно биссектрисы первого координатного угла.
относительно биссектрисы первого координатного угла.  возраcтает на D=R;
возраcтает на D=R;
 обратная функция.
обратная функция.
 б)
б)  в)
в)  г)
г) 
 . а)
. а)  б)
б) 





 где
где  равносильно
равносильно  .
. где
где  равносильно
равносильно  или
или  .
. 2)
2) 
 4)
4)  где
где 
 окрестность точки x0;
окрестность точки x0;  центр окрестности;
центр окрестности; радиус окрестности.
радиус окрестности. члены которого занумерованы натуральными числами и расположены в порядке возрастания номеров. Последовательность обозначают
члены которого занумерованы натуральными числами и расположены в порядке возрастания номеров. Последовательность обозначают  или
или  , или
, или  .
.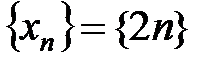
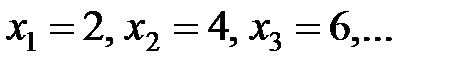
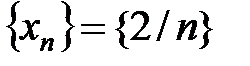
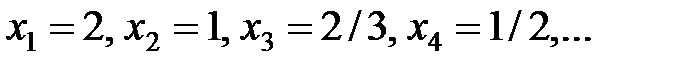
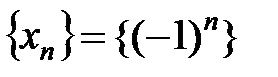
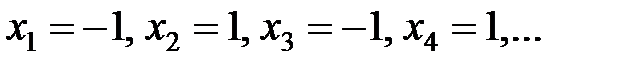
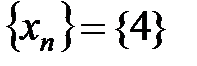
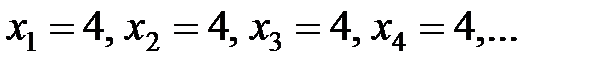
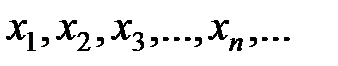
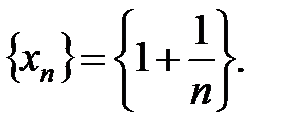
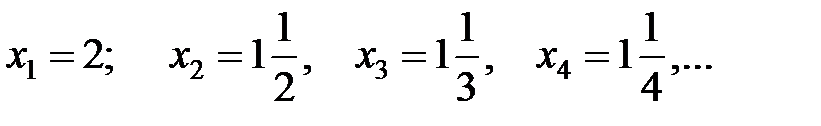
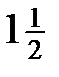 2\4
2\4 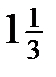 2\4
2\4 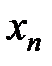 не примет значение, равное 1).
не примет значение, равное 1).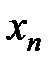 (пределом числовой последовательности), если для любого сколь угодно малого положительного числа
(пределом числовой последовательности), если для любого сколь угодно малого положительного числа 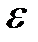 найдется такой номер N, зависящий от
найдется такой номер N, зависящий от 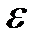 , что для всех значений
, что для всех значений 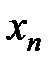 , у которых n>N, будет выполняться неравенство
, у которых n>N, будет выполняться неравенство 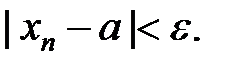
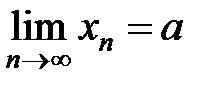 или
или 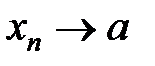 при
при